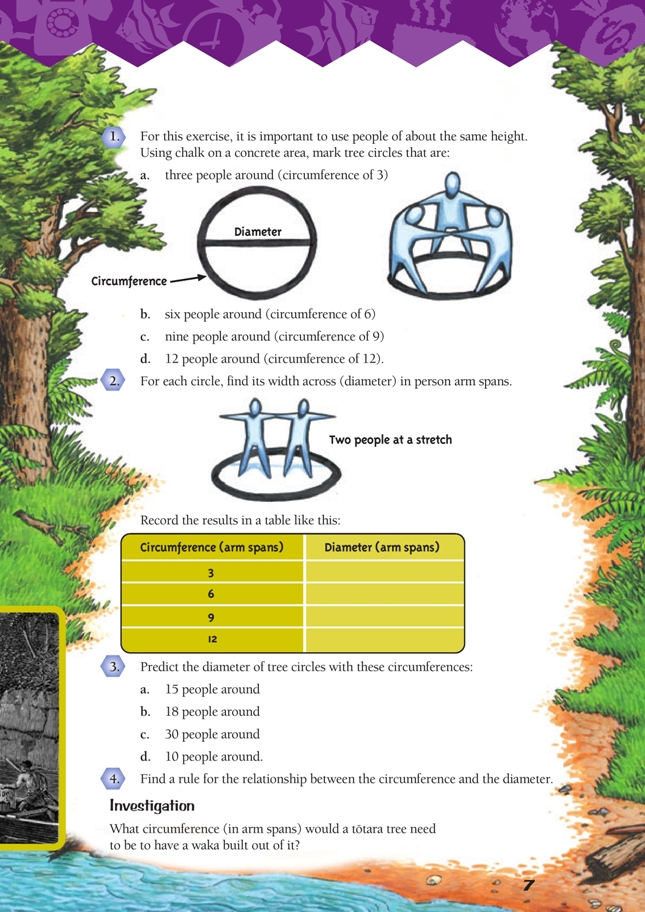
This is a level 3 algebra strand activity from the Figure It Out series.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (679 KB)
use a table to find a relationship
express a relationship as a rule
chalk
a group of classmates of similar height
This activity explores the relationship between the circumference and diameter of a circle. Where the number of students forming a circle is a multiple of 3, (3, 6, 9, 12, …), they will find that the diameter is about one-third of the circumference. For example, a tree that has a circumference of 12 arm spans will have a diameter of 12 ÷ 3 = 4 arm spans. There is variation in the heights and arm spans of students, so the relationship will be approximate. To reduce this problem, try to put the students with peers who are about the same height.
The exact numbers of times that the diameter of a circle will go around the circumference is about 3.14 and is known as “pi”. The symbol π is used to denote it.
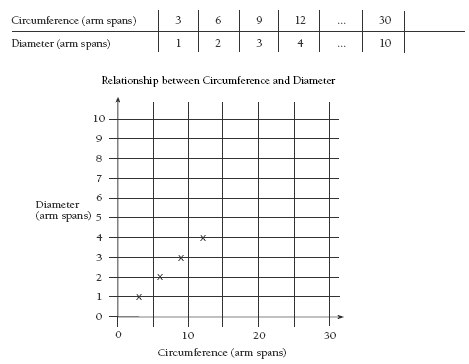
The students can use tables and graphs to show the relationship that they find using their arm spans.
Note that the relationship is linear because, when graphed, the points lie on a line.
Answers to Activity
1. Practical activity. Teacher to check
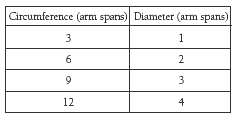
2. The approximate diameters are:
3. a. 5 arm spans
b. 6 arm spans
c. 10 arm spans
d. 31/3 arm spans
4. The circumference is approximately three times the diameter. This could be written as c = 3 x d or c = 3d.
Investigation
Answers will vary, but a waka needs to be at least one arm span wide, so the totara must be at least three arm spans in circumference.