This problem solving activity has a geometry focus.
He uses a dinner plate to draw a circle on a piece of wood and cuts out the circle using his father’s jig saw.
He now wants to find the centre of the circle so that he can attach the hands of the clock.
He heard that this can be done using a right angle but he can’t remember how.
Can you help him find a way?
- Find the centre of a circle using common material or mathematical construction tools.
For this problem that applies geometry to a ‘practical’ situation, students need to know how right angles and circles are related.
The first connection, that the angle in a semicircle is a right angle, leads to the first solution. Also, If you draw a secant to a circle and bisect that secant, the bisector goes through the centre of the circle. This produces two solutions without relying on the use of a ruler and compass.
- Copymaster of the problem (English)
- Copymaster of the problem (Māori)
- Scissors
- Cardboard (to make the circle)
- Additional constructing tools (as needed)
The Problem
Vince is making a toy clock. He uses a dinner plate to draw a circle on a piece of wood and cuts out the circle using his father’s jig saw. He now wants to find the centre of the circle so that he can attach the hands of the clock. He heard that this can be done using a right angle but he can’t remember how. Can you help him find a way?
.gif)
Teaching Sequence
- Introduce the problem to the class.
- Brainstorm ideas for approaching the problem. Ask
What do you know about circles?
Can you think of a connection between a circle and a right angle? - As the students work on the problem, in pairs, ask the following questions to extend their thinking:
What strategies helped you find the answer?
How did you know when you had the solution and could stop looking? - Share answers. Have the students write them on the board as they are given. Ask the class to use the methods to find the centre of a circle. Which do they think is the most accurate method?
- Have each student write up their own record of the solution to the problem.
Solution
First Solution: Take a large piece of paper with a right angle in the corner. Put the corner on the edge of the circle and mark where the two edges of the paper meet the circle. If these marks are joined the line passes through the centre of the circle.
If this process is repeated after putting the corner of the paper on another place on the edge of the circle, another line passing through the centre can be drawn. These lines cross at the centre.
Why does this work? This is an application of the fact that the angle subtended by an arc is a right angle if and only if the arc is a semi-circle. Because the angle in the corner of the paper is a right angle, the points where the paper touches the circle must be cut off a semi-circle. This can only be done if the line between the two points is a diameter.
Next it is clear that two different diameters can only intersect in the centre of the circle.
Second Solution: Draw an arbitrary line across the circle. Suppose that the line meets the circle at A and B. The bisector of AB is a diameter of the circle. Two such diameters meet at the centre of the circle.
(The bisector can be found using a standard construction. Make equal arcs with centres A and B. These arcs will intersect at P and Q. The line PQ is the required bisector.)
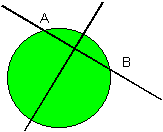
Third Solution: Draw an arbitrary line across the circle. The bisector of this line is a diameter. The mid-point of this diameter is the centre of the circle.
(The mid-point is again a standard construction. In fact, it is the same construction that produces the bisector.)