Purpose
The purpose of this activity is to support students in applying the distributive property to derive ‘new-to-them’ facts from facts they know. To succeed at this activity, students should be able to fluently recall their x 2, x 5 and x 10 facts.
Achievement Objectives
NA2-1: Use simple additive strategies with whole numbers and fractions.
Required Resource Materials
- Slavonic Abacus
- Calculator
Activity
- Introduce the students to the Slavonic abacus. An internet search for "Slavonic Abacus online" leads to many different interactive tools that could be used in the absence of a physical abacus. Explain that the colours of the beads help us to see patterns of numbers and ask students to help you spot the patterns.
- Tell the students that you are going to use the abacus to show a multiplication fact. Push across five rows of two beads, as shown.
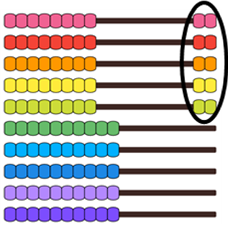
What multiplication facts am I showing? (5 x 2)
Where are the “five” and “two’ in what I have done?
Students should identify that there are “five rows of two.”
- Ask students to tell you what to do to make the abacus show 5 x 3.
Students should suggest the one needs to be added to each row.
What is the product of 5 x 3?
How do you know?
- Record the connected equations vertically and ask the students to help you look for patterns:
5 x 2 = 10
5 x 3 = 15
Can you see any patterns?
Why is the answer to 5 x 3 “five more” than the answer to 5 x 2?
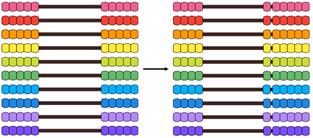
- Provide other examples to develop the idea of deriving from known facts using the distributive property. Ask for the action required to change the Slavonic Abacus model of one fact into the model for a related fact. Increase the difficulty of this task by asking students to derive products using expressions with numbers that are further apart (e.g. find the answer to 10 x 8 using the answer to 10 x 5). Record the pairs of equations vertically and look for pattern. Good examples are:
- 10 x 5 = 50 so 10 x 6 = [ ]
- 9 x 2 = 18 so 9 x 3 = [ ]
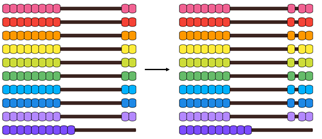
- 6 x 5 = 30 so 6 x 6 = [ ]
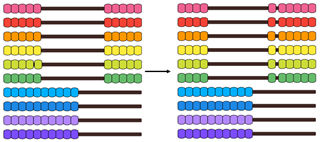
- 4 x 5 = 20 so 4 x 7 = [ ]
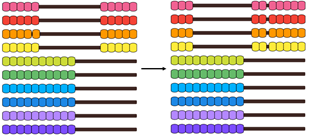
- 10 x 5 = 50 so 10 x 6 = [ ]
- Progress to providing students with paired equations without the visual support of the Slavonic Abacus. Ask students to anticipate the product of the second equation and explain their prediction. Students can manipulate beads of the Abacus to confirm their prediction. Allow students to work in appropriate groupings that will encourage peer extension, scaffolding, and productive learning conversations.
- 7 x 2 = 14 so 7 x 3 = [ ]
- 8 x 5 = 40 so 8 x 6 = [ ]
- 6 x 5 = 30 so 6 x 7 = [ ]
- 4 x 10 = 40 so 4 x 11 = [ ]
- 6 x 6 = 36 so 6 x 8 = [ ]
Next steps
- Build on the x 2 facts to learn the x 3 facts.
- Build on the x 5 facts to learn the x 6 and x 7 facts.
- Build on the x 10 facts anticipate the result of facts for x 11, x 12, etc.
Add to plan
Level Two