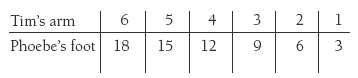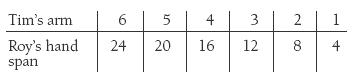Unusual Rulers

This activity integrates measurement and number by comparing some non-standard units of length as multiples and then as proportions. This can help students see the relationship between the units in different ways, depending on the strategy used in the comparison. A key idea is that the larger a unit is, proportionally fewer of it will fit in a given space in comparison with a smaller unit. For example, ten 10 centimetre lengths and twenty 5 centimetre lengths fit into the same space.
Before the students do this activity, remind them that there are 100 centimetres in a metre and have them do some quick conversions mentally:
How many metres in 200 centimetres? 300 centimetres? 400 centimetres?
and the reverse:
How many centimetres in 5 metres? 10 metres? 4.5 metres?
To introduce the problem, have the students compare the measurement strategies used by Tim, Phoebe, and Roy. Notice how Tim has transferred his arm unit to an instrument (a bamboo “ruler”) to make his measuring easier. Phoebe and Roy are using repetitions of their actual feet or hand spans to count the units.
Use the graphic showing each person’s measure of the room to compare the size of each unit. The students could transfer the graphic onto some number lines. This will help develop their concept of multiple scales. For example:

You could use suggestions such as:
Find where Phoebe’s units line up with Tim’s.
How many repetitions did she need to match 1 of Tim’s units?
Find where all the units are at the same place. Use this to help you compare the size of each unit. By following these suggestions, the students may see that Tim’s unit is 3 lots of Phoebe’s and 4 lots of Roy’s.
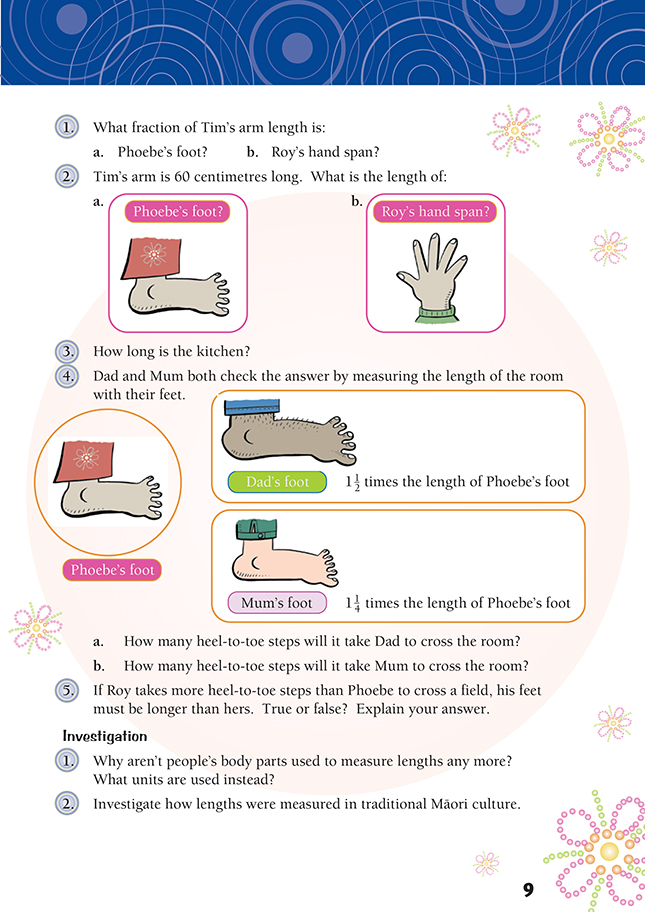
In question 1, a ratio table such as that shown in the Answers may be used to show the equivalent fractions that compare Tim’s arm to Phoebe’s foot and Roy’s hand span.
Discuss ways to use Tim’s, Phoebe’s, and Roy’s units to work out questions 2 and 3. Strategies may include adding a number line to the diagram above to show counting in 60s, for example:

The students may use number properties to answer these questions. Those at strategy stage 6 may double 60 to make 120, then add 120 + 120 + 120 = 360 centimetres. Those at stage 7 may split 60 into 6 x 10, multiply 6 x 6 = 36, and then multiply 36 x 10 = 360. The factor 6 can be split into 2 x 3. So 60 x 2 = 120, then 120 x 3 = 360.
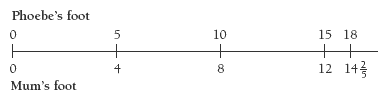
Question 4 is about the number of steps Phoebe and her father and mother will take to cross the room. The students could make a model of Phoebe’s foot with multilink or other available cubes, using 1 cube to represent 5 centimetres (her foot is 20 centimetres long, so they will need 4 cubes), and similar models to represent Dad’s foot and Mum’s foot, 30 and 25 centimetres long respectively, and use each repeatedly to answer the question:
How many steps does it take until Dad’s foot lines up with Phoebe’s and Mum’s foot lines up with Phoebe’s?
Then ask: So if 2 of Dad’s steps match 3 of Phoebe’s, how many of Dad’s will match 18 of Phoebe’s?
Comparisons can be made using double number lines (as shown in the Answers), or alternatively, all the comparisons can be made using a single table like this:

The above table is particularly useful for question 4b, where the answer involves a fraction:
So 4 of Mum’s steps match 5 of Phoebe’s. How many of Mum’s will match 18 of Phoebe’s?
Have the students share their strategies for solving this, for example: “18 ÷ 5 is 3 and a bit. That means that if Mum takes 3 lots of 4 steps, she still has to match Phoebe’s 3 last steps.” Using the table, the students should be able to see that 2 of Mum’s steps are equal to 3 of Phoebe’s steps. So Mum takes 12 + 2 = 14 steps, which has to be sensibly rounded to 15 steps.
A table like the above one can be used to make many other comparisons. You may also like to give your students rooms of different dimensions (in centimetres or metres) and ask them to say what the dimensions are using the foot lengths of Phoebe, Dad, and Mum.
Question 5 is a powerful question to see if students can explain the relationship between the size of the unit and the quantity used in the measurement task. To ensure that the students have generalised this relationship, ask them: Is it always true that the bigger the unit, the lower the number needed to measure a length?

Investigation

For the first investigation, the following prompts may be useful:
Two farmers are arguing over the position of their boundary. They both agree that it’s 30 paces from the kauri tree, but they never agree where the paces end. Why not?
What is the easiest instrument to use to measure your height accurately, a metre ruler or your hand?
Why were rulers and tape measures developed?
In some jobs, centimetres are commonly used, while in others, millimetres are used. Why is this?
For the second investigation, the website http://www.nzetc.org/tm/scholarly/tei-BesMaor-c6-1.html (Victoria University of Wellington) will provide access to an excellent description of traditional measures used by Maori.

Answers to Activity

1. a.  1/3 (because it takes 3 of Phoebe’s foot to match 1 of Tim’s arm). A ratio table might show it this way

b. 1/4 (because it takes 4 of Roy’s hand span to match 1 of Tim’s arm).
A ratio table might show it this way:

2. a. 20 cm. (60 ÷ 3 = 20)
b. 15 cm. (60 ÷ 4 = 15)
3. 360 cm or 3.6 m. You could calculate it with any or all of the children’s units. Tim: 60 x 6; Phoebe: 20 x 18; Roy: 15 x 24
4. a. 12. A double number line could be used like this:

b. 14 (rounded sensibly, this is 15 steps). A double number line could be used like this

5. False (because if his steps were longer, he would not need as many to cross the field)
Investigation
1. Comments will vary, but they should include the idea that body part sizes vary from one person to another, and this variation would lead to misunderstandings. So standardised units are needed. When the measuring task requires accuracy to a millimetre or less, body parts are simply unable to be used efficiently.
Accurate measurement also requires carefully aligning the unit to the task, which is much more difficult with body parts than with a ruler.
Efficient measurement devices like rulers can align a number of units to the object at the same time, but if we used a body part, we would have to measure by repeating a single unit.
We now use mm, cm, m, and km to measure most lengths. We could choose to use a decimetre (10 cm = 1 dm) as well as a decametre
(10 m = 1 dam) and a hectometre
(100 m = 1 hm), although these are rarely used because the basic units do just as well.
2. Some historical Māori units are: matikara: a fingerspan; tuke: the cubit from elbow to fingertip; mārò: a full arm span from fingertip to fingertip; and the kete or basket (to measure capacity).