Solve problems involving ratios.
Number Framework Stage 8
- tape measures or trundle wheels
- large protractors
- chalk
- calculators
- protractors
- rulers
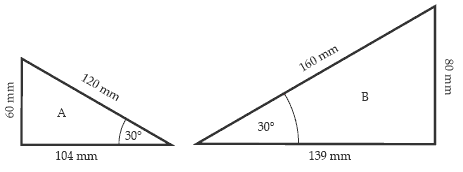
- paper right angled triangles (60mm x 104mm x 120mm and 80mm x 139mm x 160mm)
Using Materials
Give the students the two similar right-angled paper triangles. Similar means that they are enlarged or reduced copies of one another. Discuss what features of shapes helped them spot that the triangles were similar. Make a table of variant and invariant features of similar triangles, i.e., features that change and those that do not change as the triangle is enlarged.
Most students won’t know that the ratios of the side lengths within and between similar triangles remain invariant under enlargement. This concept is fundamental to understanding trigonometry.
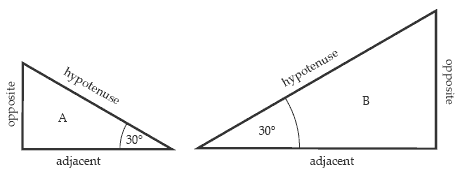
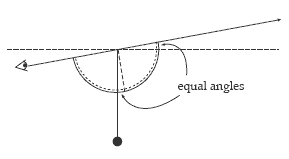
For the pair of similar triangles, first label the hypotenuse, then mark an angle and label the sides that are opposite and adjacent to that angle. Discuss the words adjacent (meaning next to), opposite (meaning across from), and hypotenuse (the side that is opposite the right angle).
Get the students to measure the side lengths of the triangles in millimetres. Stress that accuracy is important. Firstly, get the students to compare the ratios of the matching sides in the different triangles, i.e., opposite side of A : opposite side of B, adjacent side of A : adjacent side of B, and hypotenuse of A : hypotenuse of B.
For example:
The ratios 60:80, 104:139, and 120:160 contain the operator 1.33, which maps a side length from triangle A onto its matching side from triangle B. This is the scale factor.
Students might like to verify that this scale factor is constant for the matching sides of a different pair of similar triangles.
Introduce the trigonometric ratios:
sine (angle) = opposite/ hypotenuse
cosine (angle) = adjacent/ hypotenuse
tangent (angle) = opposite/adjacent
Note that these equations are algebraic, so opposite/hypotenuse means the length of the opposite side divided by the length of the hypotenuse. Get the students to use a calculator to find the value of each trigonometric ratio for the pair of similar triangles. Record the results in a table, like this:
Note there will be some measurement error, but the values should be close for each ratio [sine (30º) = 0.500, cosine (30º) = 0.866, tan (30º) = 0.577]. Tell the students that their calculator is already programmed with these numbers; this programming is activated on some calculators by entering the angle in degree mode and pressing the relevant sine, cosine, or tangent key; on other calculators, you press the relevant sine, cosine, or tangent key and then the angle in degree mode.
Have the students confirm, by checking different pairs from Material Master 7-11, that these ratios remain constant for similar right-angled triangles.
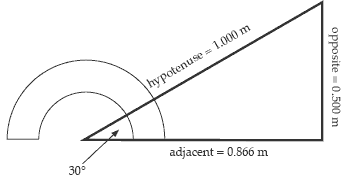
Next get the students to draw a right-angled triangle with the following specifi cations: “The sides meeting at the right angle are 500 millimetres (0.500 metres) and 866 millimetres (0.866 metres) long.” Use the large A3 protractor on the floor surface to measure angles and draw lines on the surface using a metre ruler and chalk. Ask the students to predict the angles and length of the hypotenuse of the triangle before measuring these features.
Remind the students of the formulae for the trigonometric ratios and ask how the angles could have been predicted, given sides of 0.500 metres and 0.866 metres. Tan (θ º) = opposite/adjacent , so for this triangle, the angles must have tangents of 0.500/ 0.866 = 0.577, and 0.866/0.500 = 1.732 respectively. You may like to show students how the calculator can find these angles using the inverse tangent function on the calculator (e.g., tan-1 (0.577) = 30º). Alternatively, use the table of trigonometric ratios (Material Master 7-12) and fi nd the angles that match tangents of 0.577 and 1.732.
Ask the students how the length of the hypotenuse could be predicted, given an angle of 30º and an opposite side of 0.500 metres. Because sine (30º) = 0.5, for this triangle 0.5 = 0.500/hypotenuse , so the hypotenuse must be 1.
Connect the measurements with the formulae for ratios introduced previously. For example, “If sine (θ º) = opposite/hypotenuse and the hypotenuse is 1, what is the length of the opposite side?” (sine θ º).
Tell the students to enlarge the 30º unit triangle on the floor by a factor of three by extending the hypotenuse to 3 metres. Ask them to predict the length of the opposite and adjacent sides. They should do so by multiplying each measurement from the unit triangle by three (the scale factor). Get them to check their predictions by measuring. They should also check, using their calculators, that the trigonometric ratios for these two similar triangles have remained constant under enlargement.
They should note that opposite/hypotenuse = 0.500 and adjacent/hypotenuse = 0.866 for the enlarged triangle, matching the opposite and adjacent sides of the unit triangle. The opposite/adjacent ratio for the enlarged triangle should remain 0.577 (or very close).
Ask the students how this might be useful to solve real-life problems. Tell the students that they will later use trigonometry to measure the height of the tallest trees and/or buildings in their school.
Have the students repeat this sequence for two different right-angled triangles, e.g., [90º, 45º, 45º] and [90º, 70º, 10º], firstly with an hypotenuse of 1, then using different enlargements, to establish a basis for generalisation.
Using Imaging
Provide the students with situations in which an unknown side length or angle in a right-angled triangle must be found. Besides knowing that a given triangle is right angled, students need only two side lengths, or another angle and one side length, to find out the other measures.
The scenarios might involve finding an unknown side or angle, such as building a skateboard ramp of given slope, the height of an aeroplane after takeoff, or the actual distance traveled by a climber, given the altitude and horizontal distance from base to a summit. Some of these problems can also be solved using Pythagoras’ theorem if two side lengths are known.
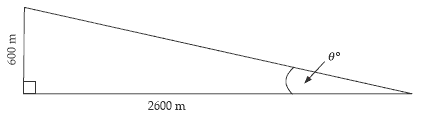
For example, “An aircraft has climbed to an altitude that is 600 metres higher than where it took off. The distance on the ground it has travelled is 2600 metres. What has been the average angle of climb for the aircraft?”
A diagram of the problem might look like this:
Students need to realise that the trigonometric ratio to be used depends on the measurements available and the measurement that is required to answer the question. In this case, the opposite and adjacent sides of the triangle are known and the angle must be found. Therefore tangent must be used, i.e., tan (θ º) = 600/2600 = 0.231 so θ º = 13º. Create a scenario that involves the students finding the heights of tall trees or buildings in their local environment. This might involve working out the clearance needed when felling a tree or the height of scaffolding needed to paint a building.
Tell the students that they can take measurements of height and angle from the ground. Introduce the clinometer as a device to measure angle of elevation. One can be made easily from a 90º protractor pasted on card, using a string and weight (two paper clips) as the plumb line.
Students may use a variety of methods. Commonly these involve scale drawing, using isosceles triangles (angles of 45º) or trigonometry. Any viable method is acceptable.
Using Number Properties
While the use of common ratios of similar triangles is a useful way to highlight the practical applications of trigonometry, it does not lead easily to trigonometric functions. The unit circle, in which triangles with a hypotenuse of 1 are drawn, does.
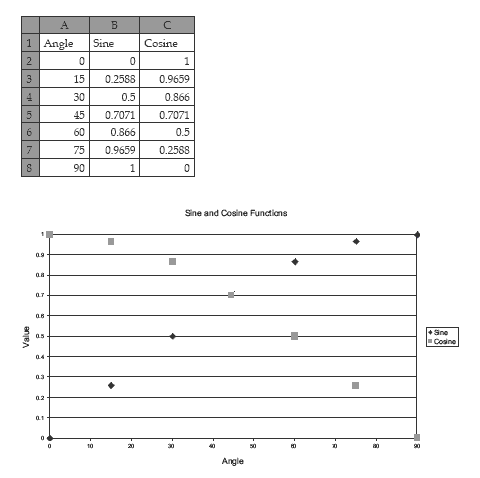
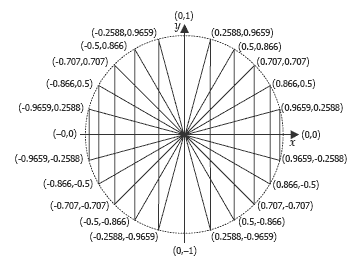
Introduce finding the sine and cosine of angles using co-ordinates on a number plane. Students will need fine graph paper to do this. Draw a quadrant number plane on the grid. Get the students to draw right-angled triangles within the first quadrant with hypotenuses of one unit (for convenience, 10 centimetres = one unit), as shown below (angles of 15º, 30º, 45º, 60º, 75º are suggested to show symmetry). Tell them to write coordinates for each vertex on the circumference of the circle.
Ask the students to connect the x and y coordinates with the sine and cosine values for the angle of the triangle at the origin (0,0). They should note that the y-coordinate gives the sine value because this is the length of the side opposite the angle. Similarly, the x-coordinate value gives the cosine value because it is the length of the adjacent side.y-coordinate gives the sine value because this is the length of the side opposite the angle. Similarly, the x-coordinate value gives the cosine value because it is the length of the adjacent side.
Ask the students what the sine and cosine values will be for 0º and 90º (sine [0º] = 0 and cosine [0º] = 1; sine [90º] = 1 and cosine [90º] = 0).
.gif)
Use a spreadsheet to graph sine and cosine as the angle varies in the first quadrant (goes from 0º to 90º).
Ask the students to describe the graphs of the sine and cosine functions and to estimate values for 10º, 20º, 40º, 50º, 70º, 80º.
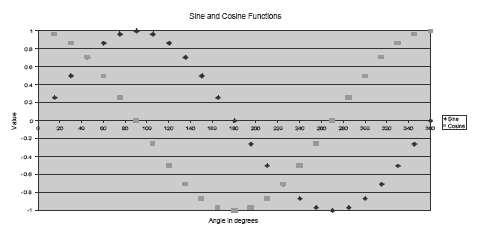
Now complete the unit circle for 15° intervals between 90° and 360° (105°, 120°,135°, …). The students will not need to make any further measurements if they usesymmetry, but they will need to attach the correct sign (+ or –) to each coordinate.
They should now enter the pairs of coordinates into their spreadsheet to get graphs of the sine and cosine functions for the angles 0° to 360°.
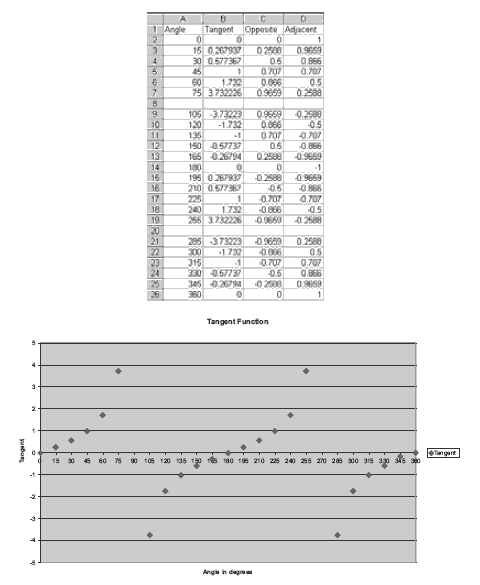
The tangent function gives the slope of a line (in the case of the unit circle, the slope of the unit radius). Slope is “vertical height divided by horizontal distance”, so the tangent value can be worked out from the sine and cosine values. The y-coordinate(sine value) gives vertical height and the x-coordinate (cosine value) gives horizontal distance, so tangent = sine/cosine
Ask the students, “For what angles is the slope of the hypotenuse equal to zero(0°, 180°, and 360°)? How do you know the slope is zero?” For 0°, 180°, and 360°, the y-coordinate (sine) is zero, so sine and cosine must be zero. For two angles (90° and 270°), the horizontal distance, given by the x-coordinate or cosine, is zero. Highlight this feature and ask, “What does this mean for the tangent of these angles?” Division by zero is undefined (a calculator will show “error”), so students should consider the tangent values for angles close to 90° and 270°. For example, the tangent gets closer and closer to infinity (+) as the angle approaches 90° from below and to negative infinity (–) as the angle approaches 90° from above.
Using this knowledge, ask the students to sketch what they believe the graph of the tangent function will look like for angles in the range 0°–360°. They can confirm their graph by using a spreadsheet to calculate the tangent from sine and cosine values and getting the program to create the graph.
Encourage the students to consider what the graphs of the sine, cosine, and tangent functions will look like for angles greater than 360°. Make the connection with rotation of the radius of the unit circle to help students understand that the graphs are cyclic, with a period of 360° (that is, the pattern repeats every 360°).