This problem solving activity has an algebra focus.
A square is transformed by increasing its length and decreasing its other side by the same percentage amount.
How does the area change?
Suppose a square is transformed by increasing its length by 10% and decreasing its adjacent side by the same amount.
What is the resultant change in area?
What if the length and adjacent side of the original square were increased and decreased by 20% respectively?
How might you quickly determine the change in area of a square given any percentage increase in length and a decrease by the same percentage in the adjacent side?
- Solve problems involving percentage increases and decreases
- Apply the area formulas for squares and rectangles.
- Devise and use problem solving strategies to explore situations mathematically (be systematic, use a diagram).
In this problem students work with area, percentages and algebra.
Parts a) and b) lay a foundation for solving the general problem.
- Copymaster of the problem (English)
- Copymaster of the problem (Māori)
- A large square to introduce the problem
The Problem
A square is transformed by increasing its length and decreasing its other side by the same percentage amount. How does the area change?
Suppose a square is transformed by increasing its length by 10% and decreasing its adjacent side by the same amount. What is the resultant change in area?
What if the length and adjacent side of the original square were increased and decreased by 20% respectively?
How might you quickly determine the change in area of a square given any percentage increase in length and a decrease by the same percentage in the adjacent side?
Teaching Sequence
- Show the students a large square and get them thinking about the properties of squares and other shapes by asking:
What shapes could I transform this square into using a single straight cut?
What attributes of this shape could I measure? How would I do that? - Pose the problem for the students to work on. Check that the students understand what is required by asking a student to restate the problem.
- Brainstorm a list of mathematical understandings that the students think may be relevant for this problem.
- As the students work, ask questions that focus on the application of percentage increases and decreases.
How did you start this problem?
How have you increased the side length by 10%?
How have you decreased the side length? - If the students have used a specific side length ask questions that encourage them to use "L".
Do you think your answers will be true for all size squares?
How could you work the problem out if you were told that the square had sides of length L? - Ask the students to prepare a written record to share with other students.
- Share answers.
Extension
What is the change in area if the length is increased by one percentage amount and the adjacent side decreased by a different percentage amount.
Solution
Let the side of the square be L. Then the area of the rectangle after transformation is given by (L + 0.1L)(L– 0.1L) = L2 – (0.1)2L2 = L2 – 0.01L2 = 99L2. Hence the change in area is a decrease of 1%..gif)
Let the side of the square be L. Then the area of the resulting rectangle is given by (L + 0.1L)(L– 0.1L) = L2 – (0.1)2L2 = L2 – 0.01L2 = 99L2. Hence the change in area is a decrease of 1%.
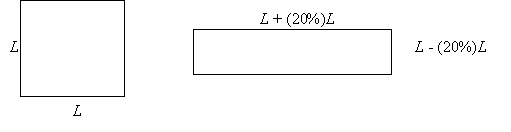
- Area of resulting rectangle is (L + 0.20L)(L– 0.20L) = L2 – 0.04L2. So the area decreases by 4%.
- The percentage change in area is the square of the percentage change in length. However, the area decreases while the length increases one way and decreases the other. The calculation is exactly the same as in a) and b) but the numbers .1 and .2 should be replaced by x, say.
Solution to the Extension
Suppose that the increase in one side is by x% and the decrease in the other is by y%. Then the new area is (L + xL/100)(L – yL/100) = L2(1 + x/100 – y/100 – xy/100). So the percentage change is x – y – xy. (A bit of algebra should convince you that if y = 1, this is always a decrease, while if y ¹ 1, then for this to be an increase we will need x > y/(1 – y).)
Note that if x = y, then the percentage change is –x2, as in c) above.
