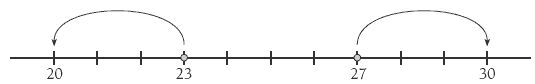Tile the Town, Tiny!

This activity involves estimating and calculating multiplication problems using multiples of 10. The students need to be able to recall groupings of 10 within numbers and round whole numbers. Many students in this transition struggle with understanding the importance of unit size in multiplication situations. This is further exacerbated by students rote learning rules such as “adding a zero” when multiplying by 10. The rule “add a zero” to multiply by 10 is conceptually inaccurate. Mathematically, adding 0 to a number doesn’t change it: 12 + 0 = 12.
The students need to be able to apply basic multiplication facts, such as 3 x 6 = 18, to other multiplication problems. For example:
30 x 60 = 18 x 10 x 10
= 1 800 (18 hundreds)
6 000 x 30 = 18 x 1 000 x 10
= 180 000 (18 ten-thousands)
300 x 0.6 = 18 x 100 x 0.1
= 180 (18 tens)
The first part of this activity is aimed at developing this kind of reasoning by having the students partition arrays. The scenario set up, using units of 10 and 100, encourages the students to consider the unit sizes of the numbers involved. For example, 30 x 120 = 3 x 12 x 10 x 10, which is 36 hundreds:

Question 4 requires the students to apply rounding to multiplicative situations to help them make reasonable estimates. Number lines can be useful for visualising what multiple of 10 or 100 a number is closest to. Question 4i gives the dimensions of a rectangle as 27 cm x 23 cm. Drawing a number line that contains these two numbers shows that 23 is closer to 20, while 27 is closer to 30.


This means that the area of the 27 cm x 23 cm rectangle can be estimated by finding the area of a 20 cm x 30 cm rectangle. The students may like to draw these rectangles on grid paper and view their areas to see that this makes sense spatially as well.
Question 5 deals with some advanced ideas about the effect of rounding and which strategy is most accurate in which situations. It all depends on the numbers.
Rounding both dimensions of a rectangle up or down produces variable inaccuracy that is proportional. For example, for a 38 cm x 29 cm rectangle, the estimate of 40 cm x 30 cm = 1 200 cm² is only 98 cm² away from the actual area, an error of only about 9%. But for a 35 cm x 26 cm rectangle, the rounded estimate is 290 cm² away, an error of 32%.
If both dimensions are mid-range between multiples of 10, it is usually more accurate to round one up and one down. Consider a 45 cm x 35 cm rectangle: rounding both numbers up gives an estimate of 2 000 cm² (an error of 425 cm² or 27%) and rounding both numbers down gives an estimate of 1 200 cm² (an error of 375 cm² or 24%). Rounding one up and one down gives an estimate of 1 500 cm² or 1 600 cm² (an error of 75 cm² or 25 cm²). In this case, rounding the bigger factor, 45, down and the smaller factor, 35, up produces the most accurate estimate.
The halfway method described by Tiny Tim in the second example in question 4 involves approximating the area of a rectangle to the area of a square. For example, to estimate the area of a 45 cm x 35 cm rectangle, Tim will use a 40 cm x 40 cm square (45 + 35 = 80.  Half of 80 is 40.) In this case, the estimate is very accurate. However, if the dimensions of the rectangle are very different (as in a long skinny rectangle), the method is very inaccurate. Using this method, the area of a 45 cm x 5 cm rectangle (225 cm²) would be estimated by finding the area of a 25 cm x 25 cm square (625 cm²).
 

Extension

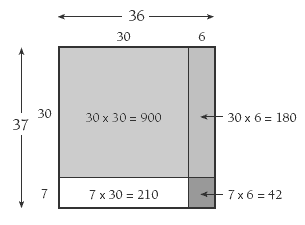
Students can learn to multiply large numbers by first splitting factors additively using the distributive property. For example, to calculate 36 x 37, both factors might be split: 36 = 30 + 6, and 37 = 30 + 7. The product is shown in this array:
So 36 x 37 = 900 + 180 + 210 + 42

More about this kind of partitioning can be found on page 37 of Book 6: Teaching Multiplication and Division in the Numeracy Project series.
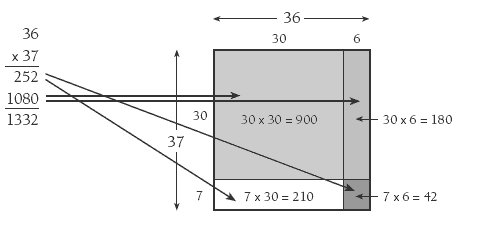
As a further extension, the students could explore the links between the partial products in written algorithms and the parts of the area diagram. For example, 36 x 37 can be solved in written form as:

You can extend this application of distributive property by asking the students to work out the answers to problems such as 347 x 28 and 4.6 x 4.5.

Answers to Activities

1. 10. (10 x 100 = 1 000)
2. Practical activity. Answers are:
a. 5 000
b. 3 600
3. a. 240
b. 4 000
c. 24 000
d. 21 000
4. The use of the strategies will vary.
i. 27 + 23 = 50. 50 ÷ 2 = 25.
25 x 25 = 625 cm²; or 30 x 20 = 600 cm²
ii. 45 + 65 = 120. 120 ÷ 2 = 60.
60 x 60 = 3 600 cm²; rounding, such as 50 x 70 = 3 500 cm²
iii. 50 x 40 = 2 000 cm²
iv. 10 x 65 = 650 cm² or 15 x 60 = 900 cm²
v. 34 + 46 = 80, 80 ÷ 2 = 40,
40 x 40 = 1 600 cm²; or 30 x 50 = 1 500 cm²
vi. 50 x 40 = 2 000 cm²
vii. 190 x 20 = 3 800 cm² or 200 x 20 = 4 000 cm²
viii. 400 x 300 = 120 000 cm²
5. a. i. 621 cm²
ii. 3 375 cm²
iii. 1 862 cm²
iv. 806 cm²
v. 1 564 cm²
vi. 1 862 cm²
vii. 4 158 cm²
viii. 120 768 cm²
b. It depends on the numbers being rounded. If both numbers are close to decades,
rounding both to the nearest decade will give a good estimate. Where the two
numbers are roughly the same amount either side of a decade, rounding one up and the other down will give a good result.
c. The add, halve, and square method gives a good result if the two numbers are fairly close. The further apart the numbers are, the less satisfactory the estimate will be. This is because the method treats a rectangle as a square.