In this unit students are asked to investigate mathematical relationships when they select various numbers to be used in a 3 circle configuration and in 6 circle configurations. They will explore both whole number and fractional numbers as they consider how various configurations impact on the relationships between numbers.
- solve simple number problems
- solve simple fraction problems involving halves and quarters using addition and subtraction
- solve fraction problems using addition and subtraction where the fractions have a range of denominators
The contexts of this unit are configurations of three and six circles but they are used as a basis for the practice of the addition and subtraction of whole numbers and fractions and for investigating mathematical relationships. Students will need to be able to work confidently with basic fractions and have a good knowledge of addition and subtraction facts.
The unit is divided into five sessions: Mathematical Play; Equal Side Sums; Consecutive Side Sums; Six Circles; and Reflecting.
Session 1: Mathematical Play
In this section students explore the central idea of the problems. They generate examples and consider the sum-relationships that develop because of their choices. This may include investigating: can the side sums be equal; can two sides be the same; can each side have a different sum; and if they are different what are the characteristics for the numbers within the circles. The circles generate discussions that are used to hone in on what might be especially interesting aspects of the problem and what might lead to interesting conjectures and even proofs (justifications).
Session 2: Equal side sums
Here they start with the simple idea that if the same number is in each circle then it generates equal side sums. But is this the only way to get equal side sums? So is there a unique way to get a particular sum? And can they get all possible sums? This leads to the exploration of using fractions in order to generate odd sums.
Session 3: Consecutive side sums
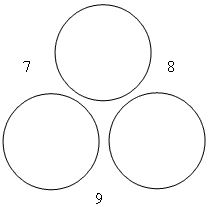
Given three consecutive side sums how do you work backward to find the numbers that must have been in the circles? Students will explore problem solving strategies such as Guess and Check. But they should be encourgaed to develop some generalisations such as finding which circle contains the smallest number. If the smallest number was between the sides with the two biggest side sums, then the other two numbers would produce a side sum that was bigger than the two biggest ones. Continuing in this way we can see that the smallest number has to be between the smallest side sums.
Let’s take the example of side sums of 7, 8 and 9 in the diagram. The smallest number has to be at the top. Suppose that we guess that this number is 2, then the bottom left number has to be 5 (to get the left side sum of 7) and the bottom right number has to be 6 (to get a right side sum of 8). But then 5 + 6 = 11. Unfortunately this doesn’t give the other side sum of 9 that we need. So try another guess until you get 3.
However, the problem of the numbers can be solved by algebraic thinking. Suppose the smallest number is blob. Then the bottom left number has to be 7 minus blob and the bottom right number has to be 8 minus blob. If you add these up you get two things. First 15 minus two blobs, and second 9, because the blobby number is the remaining side sum. So
15 minus two blobs = 9.
But then
6 minus two blobs = 0.
Surely then blob is 3.
If you prefer you could, of course, replace blob by b.
The Guess and Check and the algebra are both harder to use with the fractional cases. But since 4 = 0 + 4 = 1 + 3 = 2 + 2, it should soon become clear that with side sums of 4, 5 and 6, the numbers in the circles can’t be whole numbers. So some guessing with fractions has to be tried.
Session 4: Six Circles
With six circles a much wider range of possibilities for exploration are available. Let’s look at the equal side sums first. Clearly these can be obtained quite easily by putting the same number in each circle. But it is possible to put the numbers 1, 2, 3, 4, 5, 6 into the circles to get side sums of 9 or 10 or 11 or even 12. There is a Level 5 & 6 problem solving unit called Six Circles that you may like to take some ideas from.
What numbers can we put into the circles to get three side sums of 1? The quick answer is 1/3 six times. But can we make a side sum of 1 without using 1/3 six times? Yes. 1 = 1/2 + 1/3 + 1/6, and we can make up two sides using these numbers and the other can be completed using 1/3, 1/3, 1/3. Is this the only way to do this? No. 1 can be made up of many other fractions one of which is 1/3. For instance, 1 = 1/3 + 1/5 + 7/15 and we can make up a Six Circle with side sum 1 using 1/3, 1/3, 1/3, 1/5, 1/5, and 7/15. But can we make up a side sum of 1 using six different fractions? Yes. Recall that we can make up a Six Circle with side sum of 9 using 1, 2, 3, 4, 5, 6. Surely this means that we can make a Six Circle with side sum of 1 using 1/9, 2/9, 3/9 = 1/3, 4/9, 5/9, 6/9 = 2/3?
So it looks as if there are an infinite number of ways to get a side sum of 1 but maybe there is only one way to get a side sum of 1 if we have six different numbers in the circles? Unfortunately this is not the case. Using 1, 2, 3, 4, 5, 7 we can get an arrangement with side sums of 10. So we can get a side sum of 1 using 1/10, 2/10 = 1/5, 3/10, 4/10 = 2/5, 5/10 = 1/2, and 7/10. Maybe there are an infinite number of these that use 6 different numbers?
Reflecting: Here we use a quiz scenario for students to make up their own problems and so increase their fractional fluency.
Session 1: Mathematical Play
- With the students altogether give them the following instructions:
I want you to each take one of the Three Circle sheets (Copymaster 1) and put any numbers you like into the circles. For instance, give me three numbers. (Take some numbers from the students, say, 5, 7 and 11.) The numbers can be as big or as small as you like but you can only put one number in each circle.
Then I want you to add up the two numbers on each side of each of the Three Circle figures. (Let them find the side sums from their example. The one above gives 12, 18 and 16.) When you’ve done a whole sheet we’ll come back and discuss what things you have found. You might want to put your experiments, your mathematical play, together in a list. - Give each student a Three Circle sheet and let them work on 8 examples. Encourage them to record their various numbers and consequent side sums. As they are working check to see that everyone understands the task correctly. When the students have each produced 8 examples, bring the class together again. Find out what side sums they managed to get.
- Did anyone get three equal side sums on one of their Three Circles? (Discuss what they found.)
Did anyone get two equal side sums and a third different one on one of their Three Circles? (Discuss what they found.)
Are there any other possibilities for the three side sums? They should realise that the three side sums could all be different. Were any of these side sums consecutive like 3, 4, 5? (Discuss what consecutive means and what they found.)
In the discussions above, make sure that all the answers they have obtained are correct and list them on the board under each category. If in total only are few of any one case have been found, then the students will need to go back to work to find some more examples. - Once you have a reasonable number of examples of each type see if the class as a whole can make any conjectures about them. Here are some possibilities. When you get three equal side sums (i) you had to use the same number in each circle; and (ii) the side sums had to be even. When you get consecutive side sums you only get one even number as a side sum.
- Write these conjectures on a sheet of paper and put them on display for the rest of the week.
In the next three teaching periods, the students will investigate the various ideas that surround and extend the Three Circles.
Session 2: Equal Side Sums
- Remind the students of what had happened in the Three Circles problem in the first teaching session for the three equal side sums case.
- Can you see any patterns in the three equal side sums cases? (Discuss: the three numbers in the circles have to be the same; the side sums are always even numbers. It would be nice if they could try to justify this. For instance, if two of the numbers are different, say 5 and 9, then no third number can add to these to give the same side sum. And if all three (whole) numbers are the same the side sum of two of them can’t be odd. )
- Now take another Three Circle sheet and try to find some numbers for your circles so that the side sums will all be 5. You may have to think carefully about the sorts of numbers you use. Send the students away to work on this. If some students are able to do this by using 2 1/2 (or 2.5) in each circle, ask them to find the numbers in the circles that will give them a side sum of 9 or 11 or even 17. (If some students introduce decimals here, steer them gently back to their fraction equivalent.)
- Bring the class back to discuss what they have found. Let them realise that they can use fractions in the circles if they want to. Now specify some side sums that they have to find and let them work on these. What you ask them to try will depend on what you want them to practice but they might try to find side sums of: 1; 3; 1/2; 1/4; 3/2; 3/4; 5/4.
- Let them then spend some time on their own trying to find a side sum that can’t possibly work in the case where all the side sums are the same. Don’t tell them this but, in essence they are being asked to find a number that they can’t halve.
- Discuss as a class the problem of the number that can’t be halved. Clearly no such real number exists because we can point to a point on the number line that is half way between the point and the origin (position of zero). And this half way number is unique.
- Add any interesting observations or results to the display.
Session 3: Consecutive Side Sums
- Remind the students of what had happened in the Three Circles problem in the first teaching session in the case where the three side sums were consecutive numbers.
- Did anyone get three different side sums on one of their Three Circles? (See what they found.) Were any of these different side sums consecutive? What did we conjecture about consecutive side sums?
- Now take another Three Circle sheet and try to find some numbers for your circles so that the side sums will all be consecutive. How can you get 5, 6 and 7? Send the students away to work on this and other specific examples such as: 7, 8 and 9; 9, 10 and 11; 21, 22 and 23; 35, 36 and 37. (Note that in these cases the smallest number is odd.)
- Check that the students are getting the right answers. Then ask them to find examples where the side sums are consecutive in this way: 4, 5 and 6; 6, 7 and 8; 20, 21 and 22; 40, 41 and 42. (Note that in these cases the smallest number is even.)
- Now choose a string of consecutive numbers that involve fractions. Ask them to find examples where the side sums are consecutive in this way: 3/2, 5/2 and 7/2; 5/2, 7/2 and 9/2; 5/4, 9/4 and 13/4. Can your students see how to go from consecutive side sums to entries in the circles?
- If we are given three consecutive side sums, are the numbers in the circles unique? In other words can you get the same three consecutive numbers using different numbers in the circles?
- Can you now see how to get the numbers in the circles given three consecutive numbers? Give them a chance to think about this before discussing it as a class.
- Can you see any pattern in the numbers in the circles? Discuss.
- Display any interesting results that their work generates.
Session 4: Six Circles
- Remind the students of what had happened in the Three Circles problem in the three previous lessons. Especially remind them about the two cases considered in the last two lessons – equal and consecutive side sums.
- Now show the class the Six Circles configuration. Here we want to put any six numbers into the circles and see what we can come up with. Let them work by themselves to explore the kinds of sums that they can get using whatever numbers they want to use. They should be thinking about inserting numbers into the circles so that the side sums are all equal or are consecutive. And the numbers they use should include fractions.
- Bring them back to discuss what kinds of results they have found.
- Then get them to think about the possibility of getting a side sum of 1, of 2 or of 3.
- Bring them together to discuss their results. Also ask them if they make these with the same numbers, not all the same numbers, and six completely different numbers.
- Bring them back to discuss their results. Did you find any conjectures?
- What might you do next? This should lead them to look at consecutive sums or to consider using four circles on each side of the configuration. This is open ended. We would love to hear what results your class gets.
Session 5: Reflecting
Once again by using student input, recall what has happened in the last four lessons on this topic. In this lesson let your class have time to produce 4 questions each on the ideas around the Three and Six Circle configurations. Then divide the class into groups and let each group choose 10 of the questions that they have made up to form a quiz. Then pairs of groups should interchange their quizzes. You could work on a marking scheme of 2 marks for a correct answer; 1 mark for a small error; 0 for a completely wrong answer.
Dear Family and Whanau,
This week your child can tell you what we have been doing with numbers in circles. This has been a way of refreshing number facts around addition and subtraction. It has also been a way of thinking mathematically about the relationships between numbers. In one lesson we looked at the Three Circles configuration that we show below.
.gif)
Ask your child to explain how the side-sums are found and what observations they have made so far. Can they show you how to create configurations that have three side sums that:
- are consecutive whole numbers,
- are all the same,
- are all different?