This unit focuses on ratios that illustrate relationships between two different measures with the same unit, for example, 100g almonds for every 200g of hazelnuts. Part-whole fractions in ratios are also explored.
- Apply “times as many” relationships to sets of objects.
- Interpret “times as many” as ratios.
- Given a ratio, find relative numbers of objects.
- Given a ratio, find the relevant fractions.
- Given fractions making a whole, find the relevant ratio.
Ratios, proportions, and fractions are all related concepts that appear in both real life and mathematical situations. This unit is an introduction to ratios, and relates ratios to proportion and fractions. In mathematics, ratios and proportions are fundamental to trigonometry, coordinate geometry and calculus.
Ratio can be applied to contexts such as preparing meals for large gatherings at a Marae, interpreting the scale on a map, mixing substances like paint, fertiliser and cement, and looking for patterns and differences between groups in statistics.
Simply put, a ratio is a relationship between two measures with the same unit. For example, in making cement a worker puts in 1 measure of cement for every 4 measures of builders’ mix. The ratio is 1:4. The dry mix has a total of 5 measures, 1/5 is cement and 4/5 is builders’ mix.
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. Ways to differentiate include:
- beginning with simple ratios, e.g., 1:2, 1:3, and 2:3, and using objects like connecting cubes to model the ratios
- using symbols for ratios and fractions alongside physical and diagrammatic models
- progressing to working with the symbols alone, with the option of folding back to materials
- applying focused variation, particularly varying the number of objects while keeping the ratio the same
- asking predictive questions to encourage students to think beyond what is visible, e.g., If you make three copies of this ratio, 2:3, what ratio do you have in total?
- validating students' use of multiplication strategies, with the aim of moving them towards the use of more efficient strategies
- providing opportunities for students to work in a range of flexible groupings to encourage peer learning, scaffolding, and extension
- constructing a class chart of key ideas, models, and expressions to be used by students as a point of reference
- modelling and providing explicit teaching around the construction of tables, diagrams and graphs, and around the mathematical thinking involved in each stage of the unit. Gradually releasing your level of responsibility allows you to scaffold students towards working independently
- allowing the use of calculators for making predictions and confirming calculations, and to ease the mental load associated with calculation.
The contexts for this unit involve collections of discrete objects. The unit uses contexts like mixing fruits and nuts, and scale models. These contexts might be supplemented by, or enhanced with, other contexts involving ratios of discrete objects that are of special interest to your students. Examples might include ratios in cooking, ratios of positions in sports teams or genders in a class, ratios of colours in a smarties packet, and ratios of animals at a waterhole. Consider how you can utilise the learning in this unit as a way to make connections between mathematics and your students' 'real-world' contexts.
Te reo Māori kupu such as ōwehenga (ratio), hautanga (fraction), whakarea (multiplication, multiply), and pāpātanga (rate) could be introduced in this unit and used throughout other mathematical learning.
- Copymaster One
- Dice
- Various objects to manipulate
- A4 paper for tables
- Coloured pens
- Counters
Session 1
In this session we look at the idea of ‘twice as many’ and its variations. There are several ways to demonstrate the idea of scaling using multiplication. Adapt the contexts reflected in these problems to situations that work with the resources in your classroom, and that appeal to the interests of your students.
- Pose these problems. Use physical materials or diagrams to represent the objects in each problem.
- Here I have 6 tennis balls. Room 6 have asked for twice as many tennis balls as that. How many tennis balls do they want?
- Mary has nine coloured pencils. There are twice as many pencils in this desk. How many pencils are in the desk?
- Petra has coloured three squares yellow. If we want to have twice as many red squares as yellow squares, how many squares do we have to colour red?

- Laslo earns $43. Martine earns twice as much as Laslo. How much does Martine earn?
- Ask: What do these problems have in common?
Look for students to identify that all four problems involve “twice as many.”
What operation did you use to solve the problems?
Record the operations using multiplication:
2 x 6 = 12 2 x 9 = 18 2 x 3 = 6 2 x 43 = 86
Record the ratio 1:2
What does this ratio mean? How is it related to the problems?
Take an example, For every dollar that Laslo earns, Martine earns two dollars.
- Get the students to think about ‘three times as many’ situations. Ask them to make up ‘three times as many’ problems for others to solve. You could ask students to frame these within the same context that was reflected in the previous problems. For example, three times as many girls as boys are in the dance troupe. If there are 7 boys, how many girls are there?
- After a suitable time gather the class and share some of the problems. Physically model examples where the numbers are a reasonable size. The boy to girl problem might be shown like this, with blue cubes for boys and yellow cubes for girls:

There are 7 boys. How many girls are there? (21)
How many dancers are in the troupe altogether? (28)
What fraction of the troupe is made up of boys? (7/28)
What fraction of the troupe is made up of girls? (21/28)
What ratio is there of boys to girls? (1:3)
- Show how splitting the model can show the 1:3 relationship.
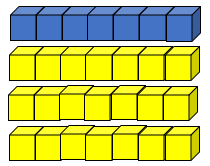
Can you simplify the fractions for boys and girls? (1/4 and 3/4).
- Tell the students that you are going to practice multiplying different numbers. Multiplication is fundamental to working with ratios. Divide the class into pairs to play the ‘times as many’ game. Give each pair of students a dice and ask each student to record the following in a table (or provide students with a copy of the following table):

Players take turns to roll the dice and nominate which cell they will fill in. Suppose a player rolls four and nominates 6 x then they put ‘six times as many as four’, 24, on their score card.
Play continues until both players fill their scoreboard. Once a ‘times as many’ option is used it cannot be used again. The player with the highest total wins.
Session 2
In this session, the concept of ratio is applied in more depth. Continue to adapt the contexts reflected in this session's problems to better suit the interests, cultural backgrounds, and current learning foci that are relevant to your students.
- Use the ‘times as many’ experience to explain the meaning of ratio.
If I have 10 blocks and you have 5 blocks I have twice as many as you and we say that the ratio of the number of blocks I have, to the number you have, is 2:1 – two to one.
- Give several examples of situations where objects are in the ratio 2:1 and 3:1
Examples might be mixing apple juice and orange juice in a 3:1 ratio or a boy to girl ratio of 2:1 in the football team.
- Once you’ve introduced the idea ask students to think of situations where the ratio is 2:1, 3:1, 4:1. It is important that the situation involves many objects not just the base ratio. For example:
In the punch bowl are 8 litres of apple juice and 4 litres of orange juice.
What is the ratio of apple to orange?
Hone kicked over 9 goals but missed 3. What was the ratio of goals to misses?
- Share the situation students create. Ask students how they can tell whether things are in the ratio 2:1 or 3:1. Expect answers like:
“There is twice/three times as many of one thing than the other.”
- Let students work in their pairs again. Ask them to draw a couple of examples where the ratio of yellow squares to red squares is 2:1 and 3:1.
Can you use more than ten squares in each ratio picture?
Secondly, ask students to make up their own ratios and draw yellow and red squares in that ratio.
- Get the class together to discuss this second task. Try to extend their concept of ratio from the simple cases of 2:1 and 3:1.
Is it possible to have ratios 3:2?
What does this mean?
Give me some examples. Suppose that Hare has apples to oranges in the ratio of 2:1 and oranges to bananas in the ratio of 2:3.
If Hare has 15 bananas, how many apples does he have?
Let students attempt the problem in pairs.
A solution looks like this:
Look at the ratio of oranges to bananas:
2:3 = □:15 meaning that 2:3 and □:15 are equivalent ratios.
□ = 10 because 15 ÷ 3 = 5 and 2 x 5 = 10. Hare has 10 oranges.
Now consider the ratio of apples to oranges:
2:1 = □:10 meaning 2:1 and □:10 are equivalent ratios.
There are twice as many apples as oranges, so the number of apples equals 20.
A ratio table can be used to track the steps. Model the construction of this, and allow students the opportunity to contribute to the filling out of the table.Apples Oranges Bananas 2 1 2 3 20 10 15 Pose a similar problem with other ratio for students to work out. For example:
Monkey has apples to oranges in a ratio of 1:3 and oranges to bananas in a ratio of 2:5.
If monkey has 12 oranges, how many apples and bananas does she have?
A ratio table of the problems is shown below. Continue to model the construction of this, whilst gradually releasing responsibility and asking students to fill out an increasing amount of the table.Apples Oranges Bananas 1 3 2 5 4 12 30 - For homework, challenge the students to find examples of ratios in real life.
Ask your parents or caregiver when they use ratios.
Session 3
In this session we look at more situations with ratios.
- Collect in students' examples of ratios from real life.
- Review the learning from the last session with the following problem:
Suppose that Hare had apples to oranges in the ratio of 2:1 and oranges to bananas in the ratio of 2:1.
What is the ratio of apples to bananas?
How can you convince me of this?
Is the ratio the same no matter how many apples Hare has? Yes.
Show this by example.
If Hare has 12 apples, how many bananas does he have? (3)
If Hare has 20 apples, how many bananas does he have? (5)
If Hare has 16 apples, how many bananas does he have? (4)
How can you explain this? Use a ratio table to show why the number of bananas is always one quarter of the number of apples. Model some of the construction of this, or ask students to complete in independently or with a partner.
Apples Oranges Bananas 2 1 2 1 4 2 1 In general, this can be shown algebraically as:
Apples Oranges Bananas a 1/2 a 1/2 a ¼ a The ratio connecting the number of apples, oranges, and bananas can be written as 4:2:1.
- Ask the students to work together on the problems on Copymaster 1.
- After a suitable time gather the class to share solutions. Note that there is more than one answer as the total number of squares can be varied.
- Share the examples of ratios that students found from real life. Use an example of a practical situation to pose a problem (perhaps draw a scale diagram in the ratio of 10:1). Model solving the problem and record the key steps of the process on a class chart/on the board.
- Ask students to use one or more of the contexts that they (and their peers) have contributed and, in pairs, create a ratio problem for another pair of students to solve. Roam and support students to ensure the problems can be solved. Ask students to solve a number of the problems posed by their peers, and then gather as a class to discuss the solutions, strategies used, challenges, and problems that they found particularly engaging.
Session 4
In this session students investigate the link between ratios and part-whole fractions.
- Get the students to work in pairs to draw and colour squares in two colours in various ratios of their choosing. (2:1, 3:1 and 5:2 would be fine.) Three different ratios are enough.
Bring the class together with their drawings.
Choose an example of a simple ratio (2:1 would be ideal).
How many squares are red?
How many squares are blue?
How many coloured squares are there altogether?
What fraction of the squares is red?
What fraction of the squares is blue?
Note with the last two questions there are different ways to express the part-whole fractions. For example, in the ratio 8:4 the fraction that is red is 8/12 or 4/6 or 2/3 and the fraction that is blue is 4/12 or 2/6 or 1/3.
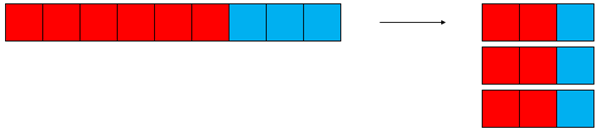
Start to draw up a table like the one below.ratio No. red squares No. blue squares No. of squares Fraction of red Fraction of blue 2:1 10 5 15 10/15 = 2/3 5/15 = 1/3 2:1 8 4 12 8/12 = 2/3 4/12 = 1/3 - Ask students for different red to blue square mixes that are in a ratio of 2:1. Illustrate how the given ratio reduces to 2:1 using diagrams. For example, consider 6:3:
What patterns do you see? (There are always twice as many red squares as blue squares. The same simplified fractions occur. There can be different total numbers of squares)
ratio No. red squares No. blue squares No. of squares Fraction of red Fraction of blue 3:2 6 4 10 6/10 = 3/5 4/10 = 2/5 3:2 15 10 25 15/25 = 3/5 10/25 = 2/5 3:2 30 20 50 30/50 = 3/5 20/50 = 2/5 What patterns do you see?
- Ask students to take one of the equivalent ratios to 2:3 and show how it simplifies by drawing pictures.
- Finish the session with this puzzle:
I have a mixture of black and white marbles in a ratio of 3:5.
There are 64 marbles in total. How many marbles are there of each colour?
Session 5
In this session students consider how part-whole fractions can be expressed as ratios.
- Remind the class of what has happened so far in this unit.
If someone was sick this week and needed to catch up, what would you tell them about ratios?
- Pose this problem for students to solve in pairs then share as a class.
Leah takes a packet of mixed nuts from the pantry.
She notices that one fifth of the nuts are brazil nuts, one third are hazelnuts, and seven fifteenths are cashews.
There are 30 nuts in the packet. What is the ratio of brazil nuts to hazelnuts to cashews?
Make sure the word version of the problem is visible and let students work in small teams to solve the problem. Provide materials, like counters if needed.
- Roam the room as students work. Look for the following:
- Do students use trial and error? If so, direct them to address the clues.
- Do students approach the task systematically and record their attempts? If not, suggest they use a table or ratio symbols.
- Do students recognise that if one fifth of the nuts are brazils then the total number must be a multiple of five?
- Do students recognise that if one third of the nuts are hazels then the total number must be a multiple of three?
- Do students recognise that the fraction “seven fifteenths” gives a strong clue about the total number of cashew nuts? (7/15 = 14/30)
- After a suitable time ask groups to prepare to share their ideas. Preparation might include writing solutions, or showing working, including diagrams. Gather the class to share ideas and address the questions above.
The solution is a ratio of Brazil:Hazelnut:Cashew of 6:10:14 that can be simplified to 3:5:7. Show the students a table containing important information in the problem but with some omissions to complete.
Total number of nuts Fraction of brazil nuts Fraction of hazelnuts Fraction of cashews Number of brazil nuts Number of hazelnuts Number of cashews 30 1/3 7/15 10 If you had this information about Leah’s bag of nuts, how would you complete the cells?
Students should comment that 1/3 of 30 equals 10 and 7/15 of 30 equals 14. They should also notice that 10/30 = 1/3.
Tell students that you are going to "go nuts" and give them another problem. They will need a blank table to keep track of the clues and find the answer.
Total number of nuts Fraction of brazil nuts Fraction of hazelnuts Fraction of cashews Number of brazil nuts Number of hazelnuts Number of cashews Three fifths of the nuts are hazelsnut.
There are 15 brazil nuts.
The total bag of nuts holds 100.
What is the ratio of brazils:hazelnuts:cashews?Total number of nuts Fraction of brazil nuts Fraction of hazelnuts Fraction of cashews Number of brazil nuts Number of hazelnuts Number of cashews 100 3/5 15 Let students work in groups to solve the problem. Roam the room to see if the students are explaining ideas to each other and justifying those ideas. For example:
The number of hazelnuts is 3/5 of 100. That is 60 hazelnuts because 1/5 of 100 equals 20.
Total number of nuts Fraction of brazil nuts Fraction of hazelnuts Fraction of cashews Number of brazil nuts Number of hazelnuts Number of cashews 100 3/5 15 60 That means the number of cashews equals 100 – 15 – 60 = 25.
Total number of nuts Fraction of brazil nuts Fraction of hazelnuts Fraction of cashews Number of brazil nuts Number of hazelnuts Number of cashews 100 3/5 15 60 25 The fractions are 15/100 = 3/20 (brazil nuts) and 25/100 = 1/4 (Cashews).
Total number of nuts Fraction of brazil nuts Fraction of hazelnuts Fraction of cashews Number of brazil nuts Number of hazelnuts Number of cashews 100 3/20 3/5 1/4 15 60 25 The ratio of Brazil: Hazelnut: Cashew is 15:60: 25 = 3: 12: 5.
- Ask different students if they have noticed any connection between fractions and ratios. Let them use a specific example, like the ratio of Brazils: Hazelnuts: Cashews of 2:3:5. What fractions are in that ratio?
Drawing a diagram will illustrate that the total of the numbers forms the denominator, and the fractions are formed by using each number as a numerator.
In the 2:3:5 ratio the denominators are 2 + 3 + 5 = 10.
The fractions are 2/10, 3/10, and 5/10. 2/10 and 5/10 can be simplified to 1/5 and 1/2.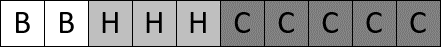
- Ask students to create their own mix of Brazils: Hazelnuts: Cashews and record their mix as fractions and as a ratio.
Family and whānau,
This week we have been investigating ratios. For homework this week students are looking for examples of ratios around their homes and reporting back. It would be appreciated if you could help your child find examples of ratios and share examples of how you may use them in your home and work (for example mixing things like cement or liquids, in cooking, or measuring). Sometimes things such as Matchbox cars or trains models will have a ratio recorded on the underside, or scales on maps, or packaging for plant fertiliser etc. Ask your child to explain what the different ratios they find mean. Students will bring their examples back to class to create a display. Thank you for your support.