This unit requires students to enlarge and reduce two-dimensional mathematical shapes by a scale factor. As students work in co-operative teams of four to complete a puzzle, they use a ruler, compass and protractor.
- Follow instructions, in diagram form, to construct two-dimensional mathematical shapes, e.g. triangles, quadrilaterals, pentagons and hexagons.
- Enlarge and reduce two-dimensional mathematical shapes by a given scale factor.
- Identify invariant properties when enlarging and reducing two-dimensional mathematical shapes.
- Convert between measures given in mm and cm.
- Multiply whole numbers by a decimal.
This unit moves students from knowing about two-dimensional mathematical shapes to being able to use them in a practical situation. The ability to accurately use a ruler, compass and protractor is the focus of the unit, along with the ability to read and work through instructions to a finished product.
This unit also introduces students to enlarging and reducing the size of two-dimensional mathematical shapes by a scale factor. Understanding what a scale factor is as well as how to work with scale factors in a practical situation are part of the unit, including invariant properties, i.e. aspects of shapes that remain the same when enlarged or reduced.
Scale factor is the amount a shape is enlarged or reduced. A scale factor of 2 means a shape doubles in size, with each length of each side doubling. A scale factor of 0.5 means the shape is halved in size. To find the length of a line changed by scale factor, the length is multiplied by the scale factor.
In this unit the centre of enlargement will not be considered.
Before this unit starts students need to know the following two-dimensional mathematical shapes and geometry vocabulary; equilateral triangle, right angle triangle, isosceles triangle, scalene triangle, quadrilateral, square, rectangle, trapezium, rhombus, parallelogram, pentagon, hexagon, octagon, perpendicular, parallel, right angle, base, interior angle, exterior angle.
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. Ways to differentiate include:
- Beginning with simple enlargements to establish the ratio relationships between lengths, before solving problems with more complex enlargements. For example, enlarge a simple figure by a scale factor of two or three.
- Explicitly model techniques such as creating intersecting arcs and measuring angles with a protractor for students who need support.
- Use calculators to reduce the burden of calculation.
- Ask students to work in collaborative teams to distribute the workload and share ideas.
The context for this unit is creating shapes from a design and enlargement. The puzzles form simple targets. The templates can by superimposed over designs that are of personal and cultural relevance to your students. For example, rectangular puzzles can be imposed onto koru or seashell pictures. Enlargement of a figure to create a poster for a bedroom is a motivating context for students.
- Compass
- Pencil
- Protractor
- Ruler
- Scissors
- Card
- Team puzzles and resources
Getting Started
Arrange the students into teams of 4, explaining that this activity involves each team making four pieces of a puzzle, then putting the puzzle together. Each student works independently to start with making one piece of the puzzle. The shape of the piece is drawn as accurately as possible, checked by another team member, then cut out. Once all four pieces are made, they are put together to make a square or rectangle.
Use the copymaster of Team Puzzle One
Hand out the instructions for Team Puzzle One, one set for each team. Cut out the four sets of instructions, so each team member gets the instructions for an individual piece of the puzzle. The piece labelled number one, is the least challenging and number four is the most challenging in each puzzle. Some instructions are in diagram form and some written. If students are unsure of an instruction, the team needs to get together and work it out.
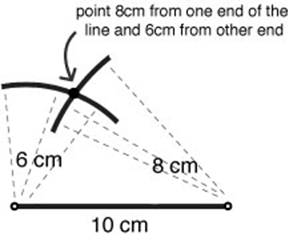
Students may need some teaching at this point, or before this activity starts, on how to use a compass to find the intersecting point of two lines of a set length. For example, How do you use a compass to draw a triangle with sides 10cm, 8cm and 6 cm long?
At the conclusion of this session when the puzzles have been completed, discuss with the class the activity. Topics that could be discussed include:
- the importance of accuracy
- what to do if you are the first in your team to complete your piece
- what to do if you have trouble understanding an instruction.
Exploring
Over the next 2 or 3 days the teams work on the remaining team puzzles. The teacher’s role during this time is to encourage and teach students and teams as the need arises. At an appropriate time teaching is likely to be needed on enlarging and reducing by a scale factor. Team Puzzles Four, Five and Six have a scale factor to work out before the puzzles pieces are drawn and cut out.
Reflecting
Have the students reflect and talk about the things they have learnt by completing these puzzles. Work on the puzzles the students have developed themselves at home.
Dear parents and whānau,
In maths we are learning about geometry and measurement. Ask your child to explain the geometric puzzles that they have been working on in class.
At home this week your child is to design a team puzzle for other teams in the class to work out. The instructions for making each puzzle piece need to be written using mathematical names of two-dimensional shapes, and need to give measurement dimensions of sides in centimetres and interior angles in degrees. Diagrams are acceptable but some written instructions must be given for each piece.
Please discuss this task with your child and see if you can follow their instructions once their puzzle is completed. Thank you for your interest and encouragement.