This unit examines the properties of polygons and how these are related. It introduces the names in both te reo Māori and English.
- Investigate properties of symmetry in shapes.
- Investigate spatial features of shapes.
- Use both English and te reo Māori to describe different polygonal shapes.
This unit allows students to develop an understanding of the geometrical features of polygons and how classes of polygons are defined. It also aims to develop aspects of symmetry (reflective and rotational) through a problem solving approach.
A polygon is a planar (flat) shape that is bounded by straight sides. The relationships between sides and angles are used to create classes (groups) of shapes. In this unit students form quadrilaterals and triangles. Each class of shapes contains sub-classes. For example, a quadrilateral might have pairs of opposite parallel sides. If a quadrilateral has only one pair of parallel sides, it is called a trapezium. If it has two pairs of parallel sides, it is called parallelogram. Some parallelograms have internal angles that are right angles. That class of shapes is called rectangles. Definition, and reasoning with those definitions, is an important feature of geometric thinking.
The learning opportunities in this unit can be differentiated by providing or removing support to students, or by varying the task requirements. Ways to support students include:
- ensuring that students have access to the physical manipulatives suggested, so they can experiment with forming and folding shapes, before being required to visualise transformations
- explicit modelling the forming, folding, reflecting, and rotating of shapes. Give students opportunities to copy your actions before attempting problems independently
- helping students to represent shape forming, reflections and rotations diagrammatically to ease memory load and support thinking, e.g. by drawing lines of symmetry on a paper copy of a shape
- providing a list of mathematical terms, and definitions for students to refer to
- using the art of storytelling to provide a motivational setting for mathematical inquiry.
Tasks can be varied in many ways including:
- beginning with simple shape problems with one or two conditions, before engaging students in tasks with multiple conditions
- using collaborative grouping (mahi tahi), particularly with physical activities, so students can support others and share ideas
- reducing the demands for a product, e.g. diagrams with less reliance on writing sentences
- altering the extent to which students need to visualise actions, or to reason abstractly with the properties of classes.
In this unit, mathematical language is also explored particularly in terms of te reo Māori. It is envisaged that such an exploration will give rise to descriptions that can incorporate both languages, to support students to make sense of defining properties of 2-dimensional and 3-dimensional shapes.
The unit begins with string geometry to set the scene for investigating shapes and their properties using folding and possible turning techniques. This progresses to an examination of regular polygons where te reo Māori terms are introduced. The concept of whānau or family is used to reinforce the fact that polygons are linked in a range of ways.
Te reo Māori language is embedded throughout this unit:
porowhita = circle
whānau = family
taparau = polygons
tapatoru = triangle
tapawhā = square
tapawhā whakarara = parallelogram
whitianga = diameter
pūtoro = radius
paenga = circumference
tapatoru rite = equilateral triangle
puku = tummy
e toru, nga tapatoru rite = made from 3 smaller equilateral triangles
tapawhā whakarara rite = a rhombus
taparara = trapezium
tapawhā rite = square
tapawhā hāngai = an oblong
koeko tapatoru = a triangular pyramid
ahu-3 = 3 dimensions
tapaono rite = regular hexagon
e ono, tapatoru rite = 6 equilateral triangles
- String or elastic to make 2-3 metre long loops
- Drawing compasses
- Paper and scissors
- Polyhedral models (optional)
Getting Started
In this session we use loops of string or elastic to form shapes according to given requirements. We then convince others that our shape meets the requirements.
- Put students into groups of 4. Consider organising these groups to contain students of mixed abilities and mathematial confidence levels. Give each group a length of string or elastic - approximately 2 to 3 metres long. Have them tie the ends of the string in order to make a loop.
- Pose the following task:
Use the members of your group and the loop of string to make a shape that has four equal sides. - Allow the students to experiment. Provide questions that focus on the symmetry of the shape and the ‘squareness’ of the corners. For example:
How did you find each of the equal length sides?
Using the string, how might you show any lines of reflective (line) symmetry?
How might you show whether the corners are right angles (without using a protractor)?
Convince another team member that your shape is correct. - Let students share their shapes before gathering the class.
What is the mathematical name for your shape?
Most groups will create squares, but some groups may create rhombi (rhombuses).
What properties must a shape have to be a square? (Four equal sides, four right angles, two pairs of parallel sides)
Are there other shapes that have four equal sides?
What are those shapes called? (Rhombi)
What are the properties of a rhombus? (“Four equal sides” is the only defining property. Note: Opposite angles are equal so there are two pairs of equal angles.)
Is a square a kind of rhombus? (Yes. It has four equal sides). - You might draw a large Venn Diagram on the floor or whiteboard to illustrate the set and subset relationship of rhombi and squares. Ask students to draw squares and rhombi to add to the diagram. This could also be done on a PowerPoint - and students could complete the Venn Diagram in pairs. Make sure that they realise that the squares, inside the smaller circle, are also counted as rhombi, since they are also inside the larger circle.

Turn various shapes so they appear differently, and ask:
Is this still a square/rhombus? Why? (Orientation does not effect the properties of the shape.) - Now challenge the groups to use the loop of string to complete this task:
Use the members of your group and the loop of string to make a shape that has four sides, two of which are parallel.
You may need to define parallel first before groups start work. Look up a definition online. Railway tracks are a good metaphor. - After a suitable time, groups can share their shapes and justify that the shape they created meets the criteria. Most groups are likely to make parallelograms or rectangles, but some may form trapezia. Each class of shape is correct.
- Define each class of shapes, first by asking students about the properties they see, then providing them with a definition.
- Parallelogram: Quadrilateral with opposite sides that are parallel
- Rectangle: Quadrilateral with four right angles
- Trapezium: Quadrilateral with only one pair of opposite sides that are parallel.
Note: In the US, a trapezium refers to a quadrilateral with no parallel sides, and some definitions of trapezium refer to at least one pair of parallel sides, therefore including parallelograms.
- Is a rectangle a special parallelogram? (Yes, all rectangles have two pairs of parallel sides, so they are all types of parallelograms).
Is a trapezium also a type of parallelogram? (A trapezium has only one pair of parallel sides, so it is not a parallelogram). - Use your loop of string to make the following triangles:
- a triangle that has no sides that are the same (scalene)
- a triangle that has only 2 sides the same (isosceles)
- an equilateral triangle.
- After making each type of triangle, the group must prove that the necessary conditions are met. Though the conditions involve side length it is important to focus attention on angles. Use 90⁰ (a right angle) as a benchmark. Most triangles that students create have angles less than 90⁰.
- Can you form a triangle with an angle greater than ninety degrees? Try. (Yes, e.g. 120⁰, 35⁰, 25⁰)
What is true about the interior angles of an equilateral triangle? (Equal angles)
Can a triangle have one right angle? (Yes) Make a triangle like that.
Can a triangle have two right angles? (No) - Ask the students to create a set of criteria for their own shape. The shape can have up to eight sides and there can be up to four criteria. Each group needs to provide a model answer to their teacher, with awareness that more than one class of shape might be possible.
- Gather as a class. Ask groups to provide their criteria while the other groups construct the shape with string or elastic. Shapes could be compared and further explored with the use of a digital tool. Search for “shape manipulatives online” to find an appropriate site.
Session 2
Over the next few sessions, students create Te Whānau Taparau (The Polygon Family) by transforming a circle. You could introduce the key ideas in this session using the book The Greedy Triangle, by Marilyn Burns. This session introduces a significant amount of te reo māori vocabulary. Always accompany these terms by their English translations and pictures/materials to support students’ understanding of the new terms.
The Circle
- This is a story about a shape from the porowhita (circle) whānau who wanted to be part of the taparau (polygon) whānau. He was a special porowhita because he was able to transform himself into other shapes by folding and unfolding. However, he needed the help of a mathematician who knew some things about geometry ... that person is you!
- Either give the students a set of porowhita, or give the students a piece of A4 paper and ask them to make the largest possible circle using drawing compasses. Discuss how the students worked out the biggest circle. If compasses are not available simply trace around a circular plate or lid.
- Discuss the attributes of a circle.
What makes a circle different from polygonal shapes, for example the triangle (tapatoru), square (tapawhā) or the parallelogram (whakarara)? - Students should note that polygons have straight sides. In fact, a polygon is a 2-dimensional shape that is bounded by three or more straight sides.
- Is a circle a type of polygon? (No. A circle is bounded by a curved ‘side’.)
What are some names that are used to describe parts of a circle? - Focus the students on:
- diameter (rangiwhitu), radius (putoro) and circumference (pae)
- the relationship between te rangiwhitu and te putoro. The radius equals half the diameter.
- It is important for students to consider the idea of a circle as a locus, an infinite set of points that meet a condition or set of conditions. Take your students outside with skipping ropes and chalk. Challenge them in teams of three or four.
Use your rope and chalk to create a perfect circle. - Students are likely to try many different techniques, but the most successful method is to emulate a "tethered pony". One student fixes an end of the rope to spot (the centre), while another walks around them with the rope kept taut. That student traces their path with chalk.
- The defining property of a circle is that it is a set of points the same distance from the centre. The length of the rope is the radius of the circle.
The relationship between pae and rangiwhitu is an extension or extra investigation, usually reserved for later levels. Pi (3.14…) is the ratio of circumference to diameter, that is the circumference equals the diameter multiplied by pi. - Return to the class and challenge your students to:
Find the centre of your paper circle. What methods can you find? - Folding the circle in half in two different orientations creates an intersection of diameters. The point of intersection is the centre.
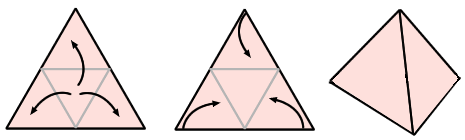
The circle becomes an equilateral triangle
We now continue the activity to transform the circle:
Porowhita looked in the mirror one day and decided he was getting bored of being a circle. Porowhita decided that he wanted to look just like tapatoru rite. He needs your help.
Using the circles (provided or made), fold Porowhita to make the biggest possible tapatoru rite (equilateral triangle). You may need to experiment with different ways of folding to get the largest one possible.- Develop a method that you will use in order to check that the shape you have made satisfies the requirements needed for a tapatoru rite (equilateral triangle), and that it is the largest equilateral triangle possible.
- If this task is too challenging for the students, you may need to give a hint (refer to the diagram) or show one that has already been made, to convince students that it can be done.
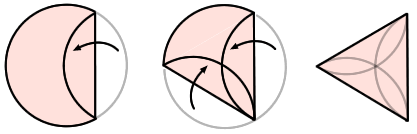
Focus the follow-up discussion on the rotational and reflective symmetry of the triangle.
How many lines of reflective symmetry does the triangle have?
Where are the lines located?Does the triangle have rotational (turn) symmetry?
Why must the internal angles be equal for the shape to have rotational symmetry?- What other types of triangle can be folded from a circle?
What happens if you do not fold into the centre of the circle?
Is a right-angled triangle possible? (One side to the triangle must be the diameter) - It would be worthwhile getting the students to develop methods to check for other tapatoru rite (equilateral triangle), and in so doing, develop the relationship between length of the sides and size of the angles.
Session 3
Triangle to trapezium
- So, Porowhita (circle) not only changes his shape, but also changes his name to Tapatoru rite (equilateral triangle). At the end of the week Tapatoru rite feels cramped - he can't roll around like he used to when he was a porowhita (circle). His aching sides and corners needed to be massaged in order to get rid of some of his pain. While lying on his puku reading the Geometers’ Weekly magazine, he spots his favourite sports hero, Jonah Trapz who is ‘built like a taparara’ (trapezium). Immediately, Tapatoru rite wishes he could transform himself into a taparara. But he needs your help.
As a possible way of introducing students to a trapezium, have them explore attributes of various trapezoidal shapes. Have them compare these with non-trapezoidal shapes including quadrilaterals that are parallelograms, rectangles, squares and others that are ‘nearly’ trapezoidal in shape. One approach is illustrated as follows:
Here is Hannah's work. She has sorted some quadrilateral shapes into two different categories: trapezia and not trapezia.Trapezia Not Trapezia Hannah states that her sorting procedure is based on the relationship between one pair of sides. If just one pair of sides is parallel, then it’s a trapezium. The other pair of sides cannot be parallel.
Do the parallel sides have to be different lengths? Why? (If the side lengths are equal then the other pair of sides will be parallel. The quadrilateral will be a parallelogram not a trapezium)- Ask the students to explore Hannah’s table of shapes and explain her sorting procedure.
Ask questions that encourage the students to focus on quadrilaterals that have one pair of parallel sides. Some students might observe that a trapezium often looks like a triangle with the top cut off leaving an edge that is parallel to the side opposite. - Tapatoru rite (equilateral triangle) wants to look like his sports hero Jonah Trapz.
Explore how you might fold Tapatoru rite (equilateral triangle) to make a taparara (trapezium).
The trapezium will contain three equilateral triangles within it, that are the same size. Let students work on the challenge in pairs.
The following diagram illustrates the change to a trapezium.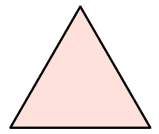
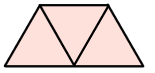
Using the taparara (trapezium) that you have made:
- How would you check that a pair of sides is parallel?
- How would you use your understanding about the equilateral triangle to help you make a convincing argument for a pair of parallel sides?
- How would you check that each of the smaller tapatoru rite are of equal size and shape, that is they are congruent?
Trapezium to rhombus
- To go with his new shape, Tapatoru rite (equilateral triangle) changes his name to Taparara (trapezium). One day, he attempts to enter the Rhombus Exhibition at the Geometrical Museum - rhombi are one of Taparara’s favourite shapes. He is stopped at the door and told that only whakarara shapes (parallelograms) may go in. Taparara really wants to get in, so he decides to change shape. He doesn’t want to be just any whakarara, he wants to be a whakarara rite (rhombus). He needs your help.
- Ask the students to fold Taparara to make a whakarara rite (rhombus). The following diagram illustrates the change from a trapezium to a rhombus:
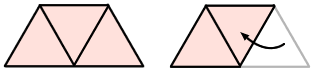
- Using the whakarara rite (rhombus) made ask:
- How would you check that the sides are parallel?
- How would you check that all the sides are of equal length?
- What might the relationship be between the angle measure of the smaller corner and the angle measure of the larger corner? (Since the triangles are equilateral, the large interior angles of the rhombus are 60⁰ + 60⁰ = 120⁰)
Of course, Taparara changes his identity and name and becomes known as Whakarara rite (rhombus). Some of his friends call him Rhombus.
Write two sentences that describe Whakarara rite’s appearance.
What fraction of the original tapatoru rite (equilateral triangle) is Whakarara rite? (One half)
Session 4
Rhombus to a triangular pyramid
- Once in the Geometrical Museum, Whakarara rite (rhombus) meets up with some of his friends, Tapawhā rite (square) and her sister Tapawhā hāngai (oblong).
- At this point the students should do some personal research and write a report, using diagrams if needed, that illustrate the difference between the rhombus (whakarara rite), the square (tapawhā rite), and the oblong (tapawhā hāngai).
Note that an oblong is a rectangle that is not a square. It has two pairs of parallel sides of different lengths, and four right angles. - Whakarara rite gets so excited by all the different diamond-like shapes that he folds into a particular diamond shape in ahu-toru (that is in 3 dimensions) called a koeko tapatoru (a triangular pyramid or tetrahedron). If you have a set of polyhedra, you will find a collection of pyramids. If not, locate a picture of one online).
- By folding the whakarara rite (rhombus) out and in, turn him into a koeko tapatoru (tetrahedron).
- The following diagram illustrates the change to a triangular pyramid.
Koeko tapatoru is not a taparau (polygon) because he is no longer flat. He is three dimensional (ahu-toru). - How would you describe his appearance now?
You might introduce some simple language of polyhedra, such as faces (flat surfaces), edges, and vertices (corners).
Triangular prism to hexagon
- Koeko tapatoru (tetrahedron) stays like this for only a short time before changing back into a whakarara rite (rhombus). A little while later, Whakarara rite stops in at his favourite food place called Geo Flatworld Takeaways to get a kai of tapaono rite (regular hexagonal shape) chips.
- Whakarara rite wants to fold into a tapaono rite (regular hexagon).
Find a way of folding to make a tapaono rite that is made out of six equilateral triangles (e ono, tapa toru rite). - The following diagram illustrates the change to a tapaono rite.
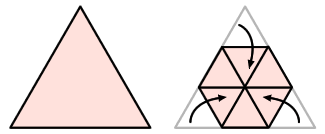
- Ask the students to check that it is a regular hexagon:
Are all the sides equal? How do you know?
Are all the angles equal? How do you know?
What rotational and reflection symmetry does a tapaono rite have? (Six lines of reflective symmetry and rotational symmetry of order six)
Session 5
In the final session we reflect on the shapes that we have explored during the week.
- At home Tapaono rite (regular hexagon) feels tired after a long day. He sits on the floor, closes his weary eyes, curls up into the frustum of a triangular pyramid and dreams about all the different shapes he was able to make ... with your expert help of course!
- Tell the students that a frustum of any solid shape is made by making a cut parallel to the base and removing the top of the solid. Show them the example of the cone.
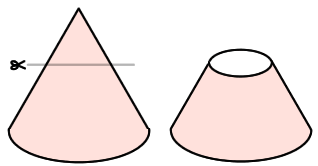
- Get the students to explore how they might ‘curl’ their tapaono rite (regular hexagon) up so that they can make such a frustum.
- Pose the following problems:
Name the different shapes of the faces of your frustum.
Make some statements about some of the attributes of the shapes that go to make up the frustum.
If Tapaono rite (regular hexagon) had sides of length two, how long were the sides of the open top and the base of the frustum?
Teaching notes:
The following diagram illustrates how to change a hexagon into the frustum of a triangular pyramid.
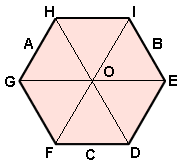
Fold B to O, then A to O, then C to O to make a triangle shape. Lift the flaps so D and E touch, F and G touch and H and I touch.
The open top has sides of length two because these sides are the same as Tapaono rite’s sides. The base sides are of length three. You can find this by measuring. (If you are clever you can use right angled triangles to work it out without measuring.)
Dear family and whānau,
This week our class has been working on polygons. We’ve talked about them in both Māori and English. If you speak another language at home, please send in the names of different shapes (e.g. triangle, quadrilateral, hexagon, rhombus, trapezium) in your home language. We can share these in class. Ask your child to describe a porowhita, a parallelogram, a tapawhā and a taparara to you.
Problems to work on
- Is it possible for a taparara to have two equal sides?
- Can you make the frustum of a square pyramid?
Note: A frustum of any solid shape is made by making a cut parallel to the base and removing the top of the solid (see cone example).
