- rautaki tatau;
- rautaki whakarōpū;
- rautaki tohatoha ōrite;
- rautaki tāpiripiri;
- rautaki whakarea māmā.
- whakoti whārite pēnei i ēnei te āhua:
- x + 2475 = 89326
- 89 326 – x = 2 475
- x – 3 827 = 2 475
- 36 × p = 252
- whakamahi, ki te tuhituhi hoki i te hoahoa rerenga me te hoahoa rerenga kōaro hei whakaoti whārite;
- tuhi whārite hei whakaoti i ētahi rapanga āhuahanga.
-
E kitea ai te otinga o ngā whārite penei te āhua x + 2475 = 89326, me huri hei whārite tangohanga, arā, 89326 – 2475 = x
- E kitea ai te otinga o ngā whārite penei te āhua 89 326 – x = 2 475, me huri te tangohanga, kia pēnei, arā, 89326 – 2475 = x
- E kitea ai te otinga o ngā whārite penei te āhua x – 3 827 = 2 475, me huri hei whārite tāpiritanga, arā, 2475 + 3827 = x
- E kitea ai te otinga o ngā whārite penei te āhua 36 × p = 252, me huri hei whārite wehenga, arā, 252 ÷ 36 = x
- Ko te tāpiritanga te kōaro o te tangohanga
- Ko te whakareatanga te kōaro o te wehenga.
he tātaitai mā ia ākonga, mā ia takirua rānei
he ngaku pepa
|
flow diagram
|
|
|
ngaku pepa
|
strip of paper
|
|
perimeter
|
|
|
operation (e.g. addition)
|
|
|
inverse operation
|
|
|
side
|
|
|
calculator
|
|
|
variable
|
|
|
rule
|
|
|
equation
|
- Ko te mahi tuatahi, he tirotiro me pēhea te whakaoti i ngā whārite pēnei i te:
x + 2475 = 89326.
Te mahi a te pouako
He tauira kōrero mā te pouako
Tuhia tētahi rapanga pēnei ki te papatuhituhi:
E taraiwa ana te whānau o Hākopa mai i tō rātou kāinga i Te Whānganui-a-Tara ki Tāmaki-makau-rau. E ai ki te pukapuka e 647km te tawhiti. Ko te kōrero a te māmā o Hakopa, kua oti te 219km. E hia te tawhiti e toe ana?
Me āta kimi te whārite i roto i tēnei rapanga. Me mahi takirua koutou ka āta whiriwhiri ai. Whakamāramatia mai te whārite.
He tāpiritanga tēnei. Ko te 647 te tapeke nā te mea koirā te katoa o te tawhiti mai i Te Whānganui-a-Tara ki Tāmaki-makau-rau. Kua oti te 219km, nō reira ka tāpirihia te tawhiti e toe ana, ka eke ki te tapeke, ki te 647. Arā: 219 + te tawhiti e toe ana = 647
Whakawhitiwhiti kōrero me pēhea te huri i tēnei rapanga hei whārite.
He roa rawa te kīanga ‘te tawhiti e toe ana’ hei tuhi ki roto i te whārite. Ko tētahi tikanga pāngarau, he whakamahi i te pū (reta) hei tohu i tētahi rahinga i te whārite. Nō reira ka whakamahia te ‘t’ mō te ‘tawhiti e toe ana’. Arā te whārite:
219 + t = 647.
Whakatauiratia te whārite ki te ngaku pepa:



Anei te pepa hei tohu i te 647, te katoa o te tawhiti. He ōrite tēnei pepa, arā, e tohu mai ana i te 647, engari kua wāwāhia te 219, koirā te tawhiti kua oti kē te haere.
He aha e tohu mai ana ki te wehenga wātea o te pepa? (Ko te tawhiti e toe ana)
Me tuhi atu te pū (reta) ki tērā wāhanga o te pepa.
Whakamāramahia te huringa o te whārite tāpiritanga hei whārite tangohanga.
Me pēhea te tātai i te rahinga o t? (Tangohia te 219 mai i te 647. E 647 te rahi o te katoa o te tapawhā hāngai. Ina tangohia te wāhanga e 219 te rahi, ka toe mai ko te t.)
I te tuatahi koinei te whārite – he whārite tāpiritanga: 219 + t = 647
Hei whakaoti i te whārite, ka hurihia hei tangohanga: 647 – 219 = t
He māmā noa iho te whakaoti ināianei. E pai ana te whakamahi tātaitai. Ko te 428 te otinga.
Hoatu ētahi anō rapanga pēnei, ko tā ngā ākonga he whakaatu ki te ngaku pepa.
$1358 kei te pēke pūtea a Waiora. Nā tōna kuia i tākoha atu ētahi anō moni, ā, ka eke te rahi o tana pūtea ki te $5827. E hia te moni i hoatu atu e te kuia o Waiora?
Anei anō ētahi rapanga hei whakaoti mā koutou. Tuhia te whārite e hāngai ana ki te rapanga. Whakatauiratia ki te pepa. Tuhia tētahi anō whārite ka whakaoti ai.
Tonoa mā ngā tamariki e tuhi tētahi rapanga e hāngai ana ki ngā whārite nei, ka whakaoti ai.
3427 + t = 6872
40 283 + p = 87 305
m + 4803 = 32 946
e + 8362 = 53 728
Anei ētahi whārite. Me mahi takirua koutou, ka whakaaro ai i tētahi rapanga pakitau mō ia whārite. Whakaotia ngā whārite.
Kia taunga haere ngā ākonga ki te huri i te whārite tāpiritanga hei whārite tangohanga, me waiho ki te taha te mahi whakatauira ki te ngaku pepa. Ko tā ngā ākonga, he whakapikitia i ngā ngaku pepa i ō rātou hinengaro hei āwhina i a rātou ki te tuhi whārite. Ka whakamāhia te tātaitai hei whakaoti i ngā whārite.
- Ko te mahi i konei, he tirotiro me pēhea te whakaoti i ngā whārite pēnei i te:
89 326 – x = 2 475.
Te mahi a te pouako
He tauira kōrero mā te pouako
Tuhia tētahi rapanga pēnei ki te papatuhituhi:
Nā te pēke i hoatu te $13 800 ki a Huriana hei hoko māna i tētahi motukā. Ko tā Huriana, he whakahoki i te moni ki te pēke. I te mutunga o te tau kei te noho nama tonu ia ki te pēke, e $7 890 te rahi o tana nama. E hia ngā moni kua whakahokia e ia ki te pēke?
Me āta kimi te whārite i roto i tēnei rapanga. Me mahi takirua koutou ka āta whiriwhiri ai. Whakamāramatia mai te whārite.
He tangohanga te whārite. Ko te 13 800 te rahi o te nama a Huriana i te tīmatanga. Ka tangohia tētahi wāhanga o tana nama, ā, i te mutunga o te tau e 7 890 te rahi. Arā te whārite:
13 800 – ngā moni i whakahokia e Huriana = 7890
Whakawhitiwhiti kōrero me pēhea te huri i tēnei rapanga hei whārite.
He roa rawa te kīanga ‘ngā moni i whakahokia e Huriana’ hei tuhi ki roto i te whārite. Ko tētahi tikanga pāngarau, he whakamahi i te pū (reta) hei tohu i tētahi rahinga i te whārite. Nō reira ka whakamahia te ‘m’ hei tohu mō ‘ngā moni i whakahokia e Huriana’. Arā te whārite:
13 800 – m = 7890.
Whakatauiratia te whārite ki te ngaku pepa:
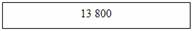


Anei te pepa hei tohu i te 13 800, te nama a Huriana i te tīmatanga. He pepa anō tēnei e ōrite ana te rahi, arā, e tohu mai ana i te 13 800, engari kua wāwāhia te 7 890, koirā te nama a Huriana i te mutunga o te tau.
He aha e tohu mai ana ki te wehenga wātea o te pepa? (Ko te rahi o te moni i whakahokia e Huriana ki te pēke)
Me tuhi atu te pū (reta) ki tērā wāhanga o te pepa.
Whakamāramahia te huringa o te whārite tangohanga.
Me pēhea te tātai i te rahinga o m? (Tangohia te 7 890 mai i te 13 800)
I te tuatahi koinei te whārite – he whārite tangohanga: 13 800 – m = 7 890
Hei whakaoti i te whārite, ka hurihia te tangohanga ki te: 13 800 – 7 890 = m
He māmā noa iho te whakaoti ināianei. E pai ana te whakamahi tātaitai. Ko te 5910 te otinga.
Hoatu ētahi anō rapanga pēnei, ko tā ngā ākonga he whakaatu ki te ngaku pepa.
E 4 280 ngā kēne waireka hei hoko mā Ani i te rā mahi moni mō tōna kura. I te mutunga o te rā, e 327 ngā kēne e toe ana. E hia ngā kēne i hokona?
Anei anō ētahi rapanga hei whakaoti mā koutou. Tuhia te whārite e hāngai ana ki ia rapanga. Whakatauiratia ki te pepa. Hurihia te whārite ka whakaoti ai.
Tonoa mā ngā tamariki e tuhi tētahi rapanga e hāngai ana ki ngā whārite nei, ka whakaoti ai.
3 427 – p = 1 089
5 073 – t = 837
45 082 – w = 28 375
436 803 – k = 78 049
Anei ētahi whārite. Me mahi takirua koutou, ka whakaaro ai i tētahi rapanga pakitau mō ia whārite. Whakaotia ngā whārite.
Kia taunga haere ngā ākonga ki te whakaoti whārite tangohanga pēnei i te 89 326 – x = 2 475, me waiho ki te taha te mahi whakatauira ki te ngaku pepa. Ko tā ngā ākonga, he whakapikitia i ngā ngaku pepa i ō rātou hinengaro hei āwhina i a rātou ki te tuhi whārite. Ka whakamāhia te tātaitai hei whakaoti i ngā whārite.
- Ko te mahi i konei, he tirotiro me pēhea te whakaoti i ngā whārite pēnei i te: x – 3 827 = 2 475.
Te mahi a te pouako
He tauira kōrero mā te pouako
Tuhia tētahi rapanga pēnei ki te papatuhituhi:
Ka tangohia e Waiora te $372.85 i tana pūtea pēke. E $284.78 e toe ana. E hia te rahi o tana pūtea i te tīmatanga?
Me āta kimi te whārite i roto i tēnei rapanga. Me mahi takirua koutou ka āta whiriwhiri ai. Whakamāramatia mai te whārite.
He tangohanga tēnei whārite. Ko te 372.85 te moni i tangohia e Waiora. Ko te 284.78 te toenga. Arā te whārite:
te rahi o te moni i te tīmatanga – 372.85 = 284.78
Whakawhitiwhiti kōrero me pēhea te huri i tēnei rapanga hei whārite.
He roa rawa te kīanga ‘te rahi o te moni i te tīmatanga’ hei tuhi ki roto i te whārite. Ko tētahi tikanga pāngarau, he whakamahi i te pū (reta) hei tohu i tētahi rahinga o roto i te whārite. Nō reira ka whakamahia te ‘r’ hei tohu mō ‘te rahi o te moni i te tīmatanga’. Arā te whārite:
r – 372.85 = 284.78
Whakatauiratia te whārite ki te ngaku pepa:


Anei te pepa hei tohu i te rahi o te pūtea a Waiora i te tīmatanga. He ōrite te rahi o tēnei pepa, engari kua wāwāhia hei whakaatu i te moni i tangohia atu me te moni e toe mai ana.
Whakamāramahia te huringa o te whārite tangohanga hei tāpiritanga.
Me pēhea te tātai i te rahinga o r? (Tāpirihia te 372.85 me te 284.78)
I te tuatahi koinei te whārite – he whārite tangohanga: r – 372.85 = 284.78
Hei whakaoti i te whārite, ka hurihia hei tāpiritanga: 372.85 + 284.78 = r
He māmā noa iho te whakaoti ināianei. E pai ana te whakamahi tātaitai. Ko te $657.63 te otinga.
Hoatu ētahi anō rapanga pēnei, ko tā ngā ākonga he whakaatu ki te ngaku pepa.
Anei anō ētahi rapanga hei whakaoti mā koutou. Tuhia te whārite e hāngai ana ki te rapanga. Whakatauiratia ki te pepa. Hurihia hei whārite tāpiritanga ka whakaoti ai.
E 3 047 ngā kēne waireka i hokona e Raniera i te rā mahi moni mō tōna kura. I te mutunga o te rā, e 694 ngā kēne e toe ana. E hia ngā kēne i a Raniera i te tīmatanga?
Tonoa mā ngā tamariki e tuhi tētahi rapanga e hāngai ana ki ngā whārite nei, ka whakaoti ai.
e – 638 = 3 027
t – 5730 = 587
k – 32 071 = 5 632
u – 25 837 = 3 784
Anei ētahi whārite. Me mahi takirua koutou, ka whakaaro ai i tētahi rapanga pakitau mō ia whārite. Whakaotia ngā whārite.
Kia taunga haere ngā ākonga ki te whakaoti whārite tangohanga pēnei i te x – 3 827 = 2 475, me waiho ki te taha te mahi whakatauira ki te ngaku pepa. Ko tā ngā ākonga, he whakapikitia i ngā ngaku pepa i ō rātou hinengaro hei āwhina i a rātou ki te tuhi whārite. Ka whakamāhia te tātaitai hei whakaoti i ngā whārite.
- Ko te mahi i konei, he tirotiro me pēhea te whakaoti i ngā whārite pēnei i te:
36 × p = 252.
Te mahi a te pouako
He tauira kōrero mā te pouako
Tuhia tētahi rapanga pēnei ki te papatuhituhi:
Ka whakakīia e Kimiora tōna motukā ki te kōhinu. E $41.34 te utu mō te kōhina, ā, e ai ki te kōrero, $1.06 te utu ā-rita. E whakaaro ana a Kimiora e hia te rōrahi o te kōhina i hokona e ia (arā, e hia rita).
Me āta kimi te whārite i roto i tēnei rapanga. Me mahi takirua koutou ka āta whiriwhiri ai. Whakamāramatia mai te whārite.
He whakareatanga tēnei whārite. Ka whakareatia te utu ā-rita ($1.06) ki te maha o ngā rita i hokona e Kimiora, ā, ka rite ki te $41.34.
Ka taea te tuhi hei whārite. Arā:
1.06 × te maha o ngā rita i hokona = 41.34
Whakawhitiwhiti kōrero me pēhea te huri i tēnei rapanga hei whārite.
He roa rawa te kīanga ‘te maha o ngā rita i hokona’ nō reira ka tuhia tētahi pū (reta), koia hei tohu mō te maha o ngā rita i hokona e Kimiora. Ka pēnei te whārite ināianei.
1.06 × r = 41.34
Whakatauiratia te whārite ki te ngaku pepa:


Anei tētahi pepa hei tohu i te katoa o te utu mō te kōhinu, arā, te 41.34.
Ko te mahi ināianei, he wehe i te pepa hei whakaatu i te utu o ia rita. Ko ia wehenga e tohu ana i te $1.06, arā, te rita kotahi. Nō reira, he wehe i te 41.34 ki te 1.06 te mahi. Arā te whārite:
41.34 ÷ 1.06 = te maha o ngā rita i hokona (r)
41.34 ÷ 1.06 = r
Whakamāramahia te huringa o te whārite whakareatanga hei wehenga.
Ka hurihia te whārite whakareatanga hei whārite wehenga. He māmā te whakaoti ināianei. Arā, ka whakamahia te tātaitai:
41.34 ÷ 1.06 = r
41.35 ÷ 1.06 = 39
Hoatu ētahi anō rapanga pēnei, ko tā ngā ākonga he tuhi i tētahi whārite whakareatanga e hāngai ana ki te rapanga, he whakaatu ki te ngaku pepa, he huri i te whakareatanga hei wehenga, he whakaoti.
Anei anō ētahi rapanga hei whakaoti mā koutou. Tuhia te whārite e hāngai ana ki te rapanga. Whakatauiratia ki te pepa. Hurihia hei whārite wehenga ka whakaoti ai ki te tātaitai.
E 7 manokaramu (kg) mīti i hokona e Rāpata, e $59.15 te utu. E hia te utu ā-manokaramu ($/kg)?
Tonoa mā ngā tamariki e tuhi tētahi rapanga e hāngai ana ki ngā whārite nei, ka whakaoti ai.
3 × m = 21.75
36 × p = 5 112
e × 17 = 144.5
t × 1.5 = 15
Anei ētahi whārite. Me mahi takirua koutou, ka whakaaro ai i tētahi rapanga pakitau mō ia whārite. Whakaotia ngā whārite.
Kia taunga haere ngā ākonga ki te whakaoti whārite whakareatanga pēnei i te 36 × p = 252, me waiho ki te taha te mahi whakatauira ki te ngaku pepa. Ko tā ngā ākonga, he whakapikitia i ngā ngaku pepa i ō rātou hinengaro hei āwhina i a rātou ki te tuhi whārite. Ka whakamāhia te tātaitai hei whakaoti i ngā whārite.
- Ko te mahi i konei, he tirotiro i tēnei mea te paheko kōaro me te hoahoa rerenga hei whakaoti whārite.
Te mahi a te pouako
He tauira kōrero mā te pouako
Whakamāramatia te kēmu ‘He aha te tau e whakaaro ana ahau?’
Ka whakaaro au ki tētahi tau. Ka whakareatia ki te 4, ka eke ki te 148. He aha te tau e whakaaro ana ahau?
Tukuna mā ngā tamariki e whakawhitiwhiti kōrero mō te huarahi e kitea ai te tau e whakaarohia ana.
He aha te mahi hei kimi i te tau e whakaarohia ana?
Whakamāramahia te tikanga o tēnei mea te hoahoa rerenga.
Ka taea tēnei kōrero te whakaatu ki te hoahoa rerenga, ki te whārite hoki. Ka whakamahia te pū (reta) t hei tohu mō ‘te tau e whakaaro ana ahau’.
t × 4 = 148
Ina tīmata ki te 148, ā, ka haere whakamuri te mahi, he māmā te kimi i te uara o t. Ka hurihia te whārite whakareatanga hei whārite wehenga. Arā:
148 ÷ 4 = t
Ka whakamahia te tātaitai, t = 37
Hoatu ētahi anō rapanga ‘He aha te tau e whakaaro ana ahau?’. Ko tā ngā ākonga, he tuhi i tētahi hoahoa rerenga, he tuhi hoki i te whārite e hāngai ana. Kātahi ka tuhia te hoahoa rerenga kōaro me te whārite e hāngai ana hei whakaoti i te rapanga.
Hei tauira:
E whakaaro ana ahau ki tētahi tau. Ina whakareatia ki te 34, ka eke ki te 476. He aha te tau?
E whakaaro ana ahau ki tētahi tau. Ina wehea ki te 17, ko te 1.5 te otinga. He aha te tau?
E whakaaro ana ahau ki tētahi tau. Ina tāpirihia te 782.7, ka eke ki te 836.3. He aha te tau?
E whakaaro ana ahau ki tētahi tau. Ina tangohia te 15 684, ko te 473 944 te otinga. He aha te tau?
Tukuna mā ngā ākonga e tuhi ētahi rapanga ‘E whakaaro ana au ki tētahi tau …’, ka hoatu hei whakaoti mā ō rātou hoa.
Kia taunga haere ngā ākonga ki te whakaoti i ngā rapanga ‘E whakaaro ana au ki tētahi tau …’, kotahi anake te paheko i roto, kātahi ka whakaurua tētahi anō kia rua ngā paheko.
Hei tauira:
E whakaaro ana ahau ki tētahi tau. Ka whakareatia ki te 1.5, kātahi ka tāpirihia te 17.6. Ko te 29.9 te otinga. He aha te tau?

t ×1.5 + 17.6 = 29.9
(29.9 – 17.6) ÷ 1.5 = t - Ko te mahi i konei, he tuhi i ētahi ture hei whārite.
Te mahi a te pouako
He tauira kōrero mā te pouako
Tuhia tētahi tapawhā rite ki te papatuhituhi, ka whakawhitiwhiti kōrero ai mō te tātai i te paenga o te tapawhā.

He aha tēnei āhua? (He tapawhā rite)
Tohua mai te paenga o tēnei tapawhā rite. E hia ngā rārangi i te katoa o te paenga? (E 4)
E hia ngā kokonga i te katoa o te paenga? (E 4)
Mehemea e 3 mitarau (cm) te roa o tētahi tapa, e hia te roa o te paenga? Whakamāramatia mai. (12cm te roa o te paenga. He ōrite ia tapa, ā, e 4 ngā tapa. Nō reira ka whakareatia te 3 ki te 4 hei tātai i te paenga)
Whakamāramatia te tikanga o te whārite hei ture mō te tātai i te paenga o tētahi tapawhā rite.
Tuhia te whārite ki te papatuhituhi. 3 × 4 = 12
I roto i te whārite, ko te 3 hei tohu i te roa o tētahi tapa o te tapawhā rite, ko te 12 te paenga o te tapawhā. Nō reira ka taea te whārite te tuhi kia pēnei: r × 4 = P.
He aha te tikanga o te r? (Koia hei tohu i te roa o te tapa o tētahi tapawhā rite)
He aha te tikanga o te P? (Koia hei tohu i te paenga o te tapawhā rite)
Whakamahia te whārite hei tātai i te paenga o ētahi tapawhā rite.
Ka whakamahia tēnei whārite hei tātai i te paenga o ētahi atu tapawhā rite. Mehemea e 56 mitarau (cm) te roa o tētahi tapa, ka whakaurua te 56 hei whakakapi i te wāhi o te r i roto i te whārite:
r × 4 = P
56 × 4 = P
224 = P
E 224cm te roa o te paenga..
Hoatu ētahi anō hei tātai mā ngā ākonga. Hei tauira:
E 4.56m te roa o tētahi tapa o te tapawhā rite. E hia te roa o te paenga?
E 13.25cm te roa o tētahi tapa o te tapawhā rite. E hia te roa o te paenga?
Tonoa ngā ākonga ki te tuhi i te whārite hei hoahoa rerenga.
Me pēhea te whakaatu i te whārite hei hoahoa rerenga.
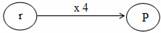
Ka tīmata ki te r, arā, te roa o tētahi tapa. Ka whakareatia ki te 4, ka hua ko te P, te paenga o te tapawhā rite.
Tuhia tētahi tapawhā rite ki te papatuhituhi, ka whakamārama ai me pēhea te tātai i te roa o tētahi tapa mehemea e mōhiotia ana te paenga.
Anei anō tētahi tapawhā rite. E 20 mitarau (cm) te roa o te paenga. E hia te roa o tētahi tapa? (E 5 cm)
Whakamāramatia mai he aha te mahi tātai i roto i tō hinengaro. (I wehea te 20 ki te 4, nā te mea e 4 ngā tapa, he ōrite te roa o ia tapa)
Tuhia hei whārite. (20 ÷ 4 = 5)
Whakamāramatia te tikanga o te whārite hei ture mō te tātai i te roa o tētahi tapa o te tapawhā rite.
Ko te 20 e tohu ana i te paenga o te tapawhā rite – ko te P hei tohu mō tēnā. Ko te 5 hei tohu i te roa o tētahi tapa – ko te r hei tohu mō tēnā. Nō reira, ka taea tēnei whārite te tuhi kia pēnei:
P ÷ 4 = r
Tonoa ngā ākonga ki te tuhi i te whārite hei hoahoa rerenga, ka whakatairite ai ki te hoahoa rerenga mō te tātai i te paenga.
Me pēhea te whakaatu i te whārite hei hoahoa rerenga.
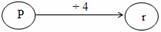
Titiro ki ngā hoahoa rerenga e rua – tētahi hei tātai i te roa o tētahi tapa, tētahi hei tātai i te paenga. He hoahoa rerenga kōaro:
- Ko tētahi ka tīmata i te r, ka hua ko te P. Ko tētahi ka tīmata i te P, ka hua ko te r.
- Ko tētahi he whakarea ki te 4, ko tētahi he wehe ki te 4
Whakamahia te whārite hei tātai i te roa o tētahi tapa o te tapawhā rite.
Hei tauira:
E 19.4m te roa o te paenga o tētahi tapawhā rite. E hia te roa o tētahi tapa?
E 27.2cm te roa o te paenga o tētahi tapawhā rite. E hia te roa o tētahi tapa?
I ngā rā ka whai muri, ka tūhuratia ngā whārite hei tātai i te paenga o ētahi atu āhua, pērā i te tapatoru rite, te tapaono rite me te tapawhā hāngai. Hei tauira:
Mō te tapatoru rite:
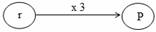
r × 3 = P (r = te roa o tētahi tapa, P = te paenga)

P ÷ 3 = r (P = paenga, r = te roa o tētahi tapa)