Talk about: One

The Talk About pages on pages 21–24 are designed for small group discussions to be followed by a whole-class round-up.

Problem One

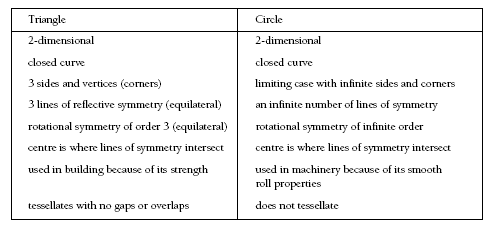
Give students about 5 minutes to discuss the similarities and differences of a triangle and a circle. Each group must have someone taking notes. You could let each group send out a “spy”, who can report back ideas from other groups. Students may choose to focus on a range of characteristics:

As a result of the whole-class round-up, a number of questions may arise that, in turn, become the subject of a whole-class investigation. Students may debate the number of sides and vertices that a circle has. It can be thought of as a polygon that has an infinite number of sides and vertices.
Students could make a table of regular polygons. From this, they will see that as the number of sides increases, the polygon becomes more like a circle:

This shows that a circle is the limiting case. The limiting case is the case which defines the limit (boundary, end point) of a process. In this instance, as the number of sides and vertices increases, the shape approaches the limiting case, a circle.

Problem Two

In this problem, students need to show that they understand the decimal system. If students consider the place values of whole numbers and decimals, they will see that division by 10, 100, or 1 000 causes the decimal point to move to the left.
For example, consider 250:

Dividing by 10 can be interpreted as “How many tens are there in ...?”
Dividing by 100 can be interpreted as “How many hundreds are there in …?”
Students can use a calculator to find out what happens to 250 as it is divided by 10, 100, and 1 000.

In the case of 25.0, 2.50, and 0.250, the zero has no effect because it is not acting as a place holder.
Students will see that there are 21/2 (2.5) hundreds in 250. Use pattern to show that 250 ÷ 1 000 is 0.250. Because 250 is a quarter of 1 000, there are 1/4 (0.25) thousands in 250.
As a number is divided by 10, the value of each digit becomes one-tenth of its previous value. This effect is best described as the digits shifting one place to the right relative to the decimal point. With division by 100, the shift is two places, and with division by 1 000, it is three places. So, consider the whole number 497:
497 ÷ 10 = 49.7
497 ÷ 100 = 4 .97
497 ÷ 1 000 = 0 .497

Problem Three

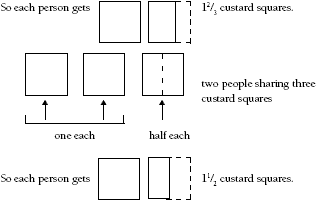
Students may wish to use a physical model of the problem, such as strips or squares of paper. An important feature is that the strips or squares used to represent the custard squares are of the same size. Using this idea:

Students will see that two-thirds is greater than one half, and therefore the three people sharing five custard squares get more.

Problem Four

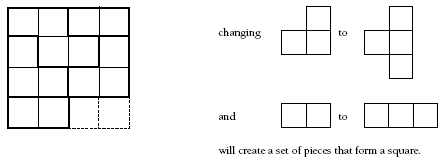
For the pieces to form a square, the total number of small squares forming the square must add to a square number (1, 4, 9, 16, 25, 36, …).

There are only 14 small squares, so two small squares must be added for the pieces to form a 4 x 4 square. Encourage students to add one square to two different pieces to make this work. A number of solutions are possible, for example:

Answers to Problems

1. Answers will vary. Comments could include:
a. The triangle has sides, but the circle does not appear to have any.
b. Both are closed figures with reflectional and rotational symmetry, and you can find the centre of both shapes.
2. a. The digits shift 1 place to the right in relation to the decimal point.
b. The digits shift 2 places to the right when dividing by 100.
c. The digits shift 3 places to the right when dividing by 1 000.
3. Three people sharing 5 custard squares get more (1 2/3 compared to a 1 1/2).
4. No. You cannot form a square because there are only 14 small cubes. There are not enough small squares to form a 4 x 4 square, and there are too many for a 3 x 3 square.