This unit builds upon the students’ experiences of making, naming and recognising common fractions using different physical representations. Its purpose is to develop understanding of fractions of sets, and the formal language and symbols associated with simple fractions and their representations.
- Read and write words and symbols for fractions.
- Introduce the terms ‘unit fraction’ and ‘proper fraction’, numerator and denominator.
- Make and understand different ways to represent 1 (whole).
- Use regional representations to find fractions of sets.
- Solve problems that involve finding the whole from a part.
- Find fractions of sets showing solutions in multiple ways including connecting fractions of sets with division.
Fractions arise from the need to divide. Division involves equal sharing or measuring. Many equal sharing situations can be solved without needing fractions. For example, 1/3 of 15 or 15 ÷ 3 can be accomplished by putting five objects in each of the three shares. However, other equal divisions of sets and objects require partitioning ones, e.g. 1/3 of 16 or 1/3 of a pie. Measurements in which the units do not fit into a space a whole number of times demand the use of fractions of that unit. For example, if a length of 13 cubes is measured with a unit of 4 cubes, 13 ÷ 4 = 3 ¼ units fit.
In this unit, students learn about fractions as numbers and as operators. Fractions are symbols in two parts, the numerator and denominator. In the fraction 3/4, three is the numerator and 4 is the denominator. The numerator, 3, is the number of parts being counted, and the denominator, 4, gives the size of those parts. Quarters are of a size that four of them make one (whole). When fractions operate on other quantities the meaning for numerator and denominator is consistent. For example, finding 3/4 of 20 involves finding 1/4 of 20 first, by dividing 20 objects into four equal parts. Three of those parts are counted, so 3/4 of 20 = 15. Note that the symbol for ‘of’ is x so the operation might be written as 3/4 x 20 = 15.
The learning opportunities in this unit can be differentiated by providing or removing support to students and by varying the task requirements. Ways to support students include:
- providing equipment such as shapes/regions, and sets of objects, so students can physically enact the operations
- helping students to record their working with diagrams, and equations, to ease demands on working memory
- easing the calculation demands by choosing fractions and sets that are manageable
- reducing the demands for a product, e.g. less calculations and words
- encouraging sharing and discussion of students’ thinking
- using collaborative grouping so students can support each other and experience both tuakana and teina roles
- encouraging mahi tahi (collaboration) among students.
The contexts for this unit can be adapted to suit the interests and cultural backgrounds of your students. Capitalise on the interests of your students. Food is appealing to most students but it is important that it is used as a ‘story shell’ not as a piece of equipment. Selection of equal teams for sports, and other activities, is a useful context for fractions of sets. Pastimes that currently engage your students, such as collectables, favourite toys, and earning money from jobs, will offer opportunities to engage them. Art and design often provide situations where shapes need to be equally partitioned.
Te reo Māori vocabulary terms such as tūtahi (whole), hautau (fraction), hautau waetahi (unit fraction), taurunga (numerator), and tauraro (denominator) could be introduced in this unit and used throughout other mathematical learning.
- Play dough
- Plastic knives
- Paper shapes
- Scissors
- Fraction Pieces
- Dice
- Plastic beans or other sharing objects like counters or cubes
- Coloured cubes/tiles (at least 4 different colours)
- Copymaster 1
- Copymaster 2
- Copymaster 3
- Copymaster 4
- Copymaster 5
Session 1
The purpose of this session is to learn how to make and represent equal parts and to read and write words and symbols for fractions. The formal language of ‘unit fraction’ and ‘proper fraction’ is also introduced.
Activity 1
- Begin by placing a length of play dough and a plastic knife in a place where all students in the group (class) can see. Distribute word cards (only) from Copymaster 1 to each pair of students.
- In their pairs ask students to discuss how they would make the equal part on their word card, if they were to use the play dough. Choose several students to explain their strategy to the group. Look for two main strategies:
- Equal partitioning by halving (symmetry), e.g. Halving halves to get quarters
- Iterating, estimating the part size and mapping it end on end to see if it works
- Listen for, and highlight a description of, the number of cuts that will be made and the language of equal parts, e.g. Three cuts creates four equal parts called quarters.
- Make sure each play dough length is the same so there is a uniform whole. Use the fraction cards to compare two fractions. Discuss which fraction is largest. You might cut play dough lengths to confirm predictions.
Is there a way to look at unit fractions like these and know which fraction is larger?
Do students recognise that a smaller denominator means the whole is cut into less parts so the parts are larger? - Use the play dough fractions to make non-unit fractions as well, such as three quarters and five eighths. Non-unit fractions have a whole number more than one as the numerator.
Activity 2
- Randomly distribute symbol cards (Copymaster 1) to the student pairs. You will need to split the class into two groups of pairs and provide each group with a full set of cards. Have students discuss the symbol and, if possible, agree about how to read it.
- Pairs display, and read, their word cards aloud to the group, one at a time. As they do so, the pair that has the matching symbol card offers it to the holders of the word card. The donor pair must explain why they are giving the symbol to the word holder pair. Can they give clear explanations of the symbolic representation of the fractional part? Model this if necessary.
Highlight the fact that each of the symbols is known as a unit fraction because it has 1 as the top number and it tells that there is just 1 of the equal parts being referred to (highlight the fact that one quarter and one fourth are different names for the same part).
Activity 3
- Make a range of shapes, made from coloured paper, available to the students. Copymaster 2 could be used if you prefer.
- Explain that they are to select a paper shape each and fold it to make a fractional part matching their word and symbol, then write the word and symbol on each of the equal parts. Encourage them to consider which shape would be the best to choose, given their fraction. For example thirds of equilateral triangles are easy to fold. Fifths of pentagons, eighths of octagons, etc. are easy to find after the centre of the polygon is located. Seventh and ninth parts are challenging. Choosing a paper strip might be wise and a strip in halves can be used to simplify the challenge.
- After students select, fold, and label their fractions of a shape, ask them to consider what they would do if the shape was different.
Can a triangle be folded into quarters when each part must be equal? - Encourage those who finish quickly (for example those with 1/2 or 1/4) to complete the task with a different shape, or, try a more difficult unit fraction.
- Let your students pair share their results, then have a korero as a class/group about why some fractions were easier to fold than others. Discuss how students approached the ‘trickier’ fractions. Highlight halving as a useful way to simplify the challenge.
- Ask your students to cut the shapes into their fraction parts. Put the pieces into an empty box and give the pieces a solid shake. Use monitors to deliver a collection of pieces to each pair.
Your job now is to reconstruct what the whole looked like for each piece you have.
What information do you have to help you?
Let students work out the appearance of the original whole for each fraction piece they have. Be aware that there are multiple possible answers depending on how the pieces are arranged. It is an excellent challenge to create as many different wholes as possible for a given fraction piece.
Activity 4
- Ask all your students to fold a paper strip into tenths, and write 1/10 on each of the equal pieces. Cut the strips into tenths.
Why are these pieces called tenths? (ten equal parts make one whole)
Where have you encountered tenths? (Students may connect to money and decimals in general) - Count in tenths with students laying the pieces down end on end as they count, ”One tenth, two tenths, … ten tenths.”
What comes next?
How might we write eleven tenths? (11/10 or 1 1/10) - Write ‘unit fraction’ on the class/group chart. Repeat and write the explanation that any fraction with a top number of 1 is called a unit fraction because it is a single piece. Add the words ‘proper fraction’ to the group chart, explaining and recording that a fraction in which the top number is smaller than the bottom number is called a ‘proper fraction’. Record “Improper Fraction”.
If 11/10 is an improper fraction I wonder what that means? (numerator is greater than denominator) - Write 3/10 on the class chart. Ask students to take 3 of their tenth pieces and write the words and symbols for these three parts. Discuss and model the fraction symbol as appropriate, highlighting the fact that the bottom number tells us how many equal parts make one (ten), and the top number (3) tells us how many of those equal parts we have chosen.
Also point out that often we see the flat line separating these numbers (this line is called the vinculum) shown with a horizontal or sloping line like this, 1/2, 1/4. - Write other non-unit fractions with tenths on the chart, having students take that many tenths and recording the appropriate words and proper fraction.
What parts would we get if we folded tenths in half?...in quarters? …in tenths? The last fold produces hundredths.
Activity 5
Conclude this session by writing the words and symbols for common unit fractions and some other proper fractions. Brainstorm on the class chart/book what has been learned about fraction symbols. Explicit links can be made here to Kupu Māori.
Session 2
The purpose of this session is to introduce the language of numerator and denominator and practise using and interpreting fraction symbols. Students work from whole to part and part to whole. An understanding of different ways of showing one whole is also developed.
Activity 1
- Distribute the cards from Copymaster 1 and have each student read out their card. As they listen they should identify the person with a matching card. This person becomes their partner for this session.
- Introduce a Fraction Dictionary.
Write 'numerator' in the dictionary. Explain that it is the top number in a fraction. Have several students come up and write their favourite fraction and circle in a different colour the top number.
Ask student pairs to discuss what the job of the top number is and to suggest a definition of 'numerator'. Numerator means the counter so that number represents the number of parts that are chosen.
Write 'denominator'. Read the word together, and discuss the meaning. It is important that students know that denominator represents the size of parts, how many of those parts make one.
Have several students again write their favourite fractions, this time writing over the denominator number in a different colour (not the same as that used for the numerator).
Activity 2
- Make sets of Fraction Pieces available to the students.
Pose and write on a chart the question:
Can the numerator in a fraction be the same as the denominator? - Use the fraction pieces.
Who can make fractions where the numerator and denominator are equal? - Let students make fractions like 2/2, 3/3, 4/4, etc. Do students notice that the fractions are equivalent to one (whole)?
Explain why any fraction where the numerator and denominator are equal is another name for one.
Can the numerator be greater than the denominator? - Ask students to make improper fractions, such as 3/2, 5/3, 7/4, etc…
What is true of all fractions where the numerator is greater than the denominator? (All improper fractions are greater than one [whole]).
Activity 3
Have students play Roll for 3 in pairs.
(Purpose: To make one from equal parts and recognise the equivalent fraction notation) Students each need a Fraction Pieces page. The game is played in pairs or threes.
- The players take turns to roll a standard dice and colour in that many parts of one of the circles they have selected. For only one roll they can nominate the number they get on the dice (1-6). It is best to keep that option until the last roll as they must complete each circle exactly.
- The winner is the player who is first to complete their circles and has correctly recorded each one (whole) as a fraction, e.g. 3/3, 8/8, once each circle is complete.
The important rule is that they can colour fewer parts and keep building to make one whole, but they must, at some point, roll the exact number needed to complete a whole.
For example, Player One rolls 6. She colours 6/8 of her circle divided into eighths. On her next turn she rolls 3. She cannot use this to complete her eighths circle because 6/8 + 3/8 is more than 8/8 (1 complete circle). She must roll 2 or two 1s in different rolls to compete 1 exactly. She can however work on her tenths circle and take 3/10 and add this to her 1/10. - Emphasise that the students should record their fraction additions.
Activity 4
Introduce the game Fraction Snap. (Copymaster 3).
- Hold up selected pairs of cards from Fraction Snap asking the students to decide for themselves if the two cards match. If so they slap the ground as if playing Snap. Discuss examples of correct ‘Snaps’ so the game is well understood.
For example: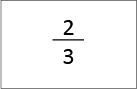
 is a pair, and so is
is a pair, and so is 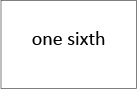

- Play Fraction Snap with a full set of cards (Copymaster 3).
- Each player takes a turn to turn up a card from their pile and place it face up in the centre of the group. As a student adds their card to the pile of face up cards, all players watch closely and are ready to say ‘Snap’, quickly putting their hand on the pile if the played card matches the one that was top of the face up pile. The first player to say ‘Snap” collects the pile and adds it face down to the bottom of their existing pile.
- The game continues until one person has all the cards or until players decide to stop.
Session 3
The purpose of this session is to use materials to develop an understanding of fractions of sets. Equal sharing of sets is linked to regions models of fractions. Children make connections with equal sharing experiences in their own lives.
Connections between repeated addition and multiplication are made as part-to-whole fraction problems are explored.
Activity 1
- Make recording material available to the students.
Distribute a shape from Copymaster 4 to each student.
This activity requires students to work from part to whole rather than the usual whole to part requirement. - Explain that each shape is a fraction or part of a whole shape. Ask students to show, with drawings, what each whole shape might look like. Model an example and show they can cut out each shape then draw around it. (Alternatively attribute blocks or foam geometric shapes can be used. The students will need to be told what fraction of the whole they are working with.)
- Give the students the opportunity to explore the problems before prompting with questions like, “If that is 1/4 of the shape, how many pieces like that will be in the whole shape?” or, “Do you think that there might be another way to show the whole shape?”
- Have students complete their drawings, writing the unit fraction in each part and an equivalent fraction for 1 beside their drawing (eg. 4/4, 2/2). Have them buddy share their results. Challenge the students to see how many ‘1’ shapes they can make for any single fraction piece.
For example if this is 1/4: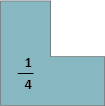
the whole shape might look like any of these: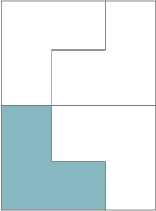


Have students find multiple solutions with the other shapes, writing the fraction in each part and the one whole fraction (4/4, 8/8 etc.) beside the whole shapes.
Activity 2
- Make plastic beans available to the students.
Have the students each take up to 4 beans and place them on their coloured fraction piece.
- Explain that these beans, like their shape, are just a fraction of a set of beans. It’s the same fraction as the fraction shape they have (1/4, 1/3, 1/2 etc.). Pose the question:
If this is a fraction of the set, how many beans are in the whole set?
- Give the students the opportunity to explore the problem before prompting with questions like, “How many quarters are in a whole set?” “How can you use your shape pictures to help you work out how many beans would be in the whole set?” If the students' exploration is unsuccessful, stop the class/group and model an example, by putting the same number of beans on each of the fraction parts in the drawing of the whole shape and skip counting (or if appropriate multiplying) to reach a total.
- Model and record several examples on the class/group chart.
For example : 1/4 of a whole set is 3 beans, 4/4 make 1 whole, so 4 lots of 3 beans will make 1 whole set.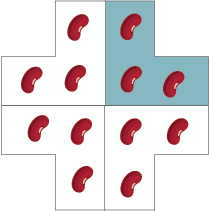
“3, 6, 9, 12” or “4 x 3 = 12” - Discuss efficiency, that is which method of calculation requires the least amount of work. Have students explore and record at least 3 more examples using different fractions and shapes and different small amounts of beans.
Activity 3
- Conclude this session by asking students to give examples of when someone has shared with them and they had received an equal part of a whole set of something.
- In the class book record some of the students’ story examples: For example:
Mia’s friend Amy gave her 1/2 of her jellybeans. Mia had 5. How many did Amy have altogether before she shared?
Tony received 6 pretzel sticks from Tama who told him he’d given him 1/3. How many did Tama have to start with?
Encourage the students to picture these fractional amounts and what the whole amount might look like. Ask students to describe what they pictured in their minds.
Session 4
The purpose of this session is to use materials to reinforce the whole to part relationship and to continue to use fractions of regions to build an understanding of fractions of sets. The key connection is made with the operation of division. One view is to see how many equal sets can be made from the starting set, and to work out the number of items in each equal set. This is called partitive division.
Activity 1
- Begin this session by reviewing Session 2, posing some fractional part to whole contextual problems.
For example: You were given 6 cherries. This was one third of the total in the bag. How many were in the bag to start with?
Your whānau were given 4 kūmara. This was one sixth of the total kūmara in the hāngi.
How many were in the hāngi to start with? - Encourage students to image the problem and solution, but if appropriate, have a student model with an appropriate drawing.
- Repeat with several examples, highlighting repeated addition and multiplication as strategies for reaching a solution. Discuss and emphasise the efficiency of multiplicative strategies that are expected at Level 3.
Activity 2
- Have the students collaborate (mahi tahi) in pairs with recording materials available.
- Pose the problem: Here is a container of strawberries. There are 12 berries in the container. You share the 12 berries equally between the two of you. How many strawberries will you each get? What is 1/2 of 12?
Show and write how you work out your share, using pictures, words and symbols. - Pose several more examples with different numbers in the container: What is half of: 14, 20, 21, 25?
- Give the students time to draw, record and write about their sharing. Explain that these will be shared with other students and displayed.
Change the number of shares and starting number of strawberries to add more challenge. For example:
1/3 of 24 1/5 of 30 1/8 of 64 1/6 of 42 1/7 of 42
Activity 3
- Have students share their work and comment on any examples where they use fractions of regions (a shape divided into halves) to support their calculations. Imaging of sharing, or simply calculating with numbers are signs of increasing sophistication.
- On the class chart write:
Half of twelve
12 shared between 2
12 ÷ 2
12/2 - Take time to discuss the important connections between these ways of recording. Highlight:
- half of twelve is a two-way equal share of 12
- when 12 is shared with two people we can write 12 ÷ 2 = 6
- ÷ is the sign for division. It looks a bit like a fraction itself
- 12/2 also means twelve shared between two. It also means 12 halves which makes a total of 6 ones.
- In sharing both 21 and 25 between them, the student pairs will have had to share 1 of the strawberries and will have written 1/2. Highlight that we read this as ‘one half’ and that this symbol is also showing 1 ÷ 2, or 1 shared between 2.
The symbol is an expression of both the problem itself and the quotient (resulting share).
These key ideas about mathematical notation should be regularly reviewed. - Transfer these ways of recording to the more complex example, such as 1/3 of 21 or 1/8 of 24
Activity 4
- Remind students how they used shapes (regions) in Session 3 to help solve problems. They may find the shapes useful now.
- Now pose equal sharing word problems such as:
12 strawberries shared between 3 people, 1/3 of 12 (or 12/3)
16 shared between 4, or 1/4 of 16 (or 16/4)
20 ÷ 5, or 1/5 of 20 (or 20/5)
21 ÷ 4, or 1/4 of 21 (or 21/4) - Have students use pictures, words and symbols to record their solutions to the problems. Have students pair share their work.
Activity 5
Pairs of students can be challenged to write their own fraction problems for their partner to solve.
Session 5
The purpose of this session is to develop a conceptual understanding of finding a non-unit fraction of a set. The language introduced in this unit is consolidated.
Activity 1
- Begin this session by highlighting strengths of some of the student work from Session 4, noticing the way they have drawn their diagrams and recorded their ideas using words and symbols.
Make coloured beans or other objects to be shared, and paper available to pairs of students. - On the class chart write and pose this problem:
There are 25 beans in a packet. You plant 2/5 of the beans. How many beans do you plant? - Ask students to solve this problem in pairs, using equipment as required. Require them to record their strategies and share their methods and answers (solutions) with another pair.
Do students recognise that finding one fifth of 25 is needed first?
Do they build two ‘iterations’ (copies) to make two-fifths?
Are their strategies only equipment based or do they use numbers and operations to anticipate the result? - Record on a chart students’ methods for solving the problem.
For example: First you have to find one fifth so you divide 25 by five. You’re asked for two fifths so you have to add two fifths together or times one fifth by two. You write this 25 ÷ 5 = 5, 5 + 5 = 10 or 2 x 5 = 10
Notice who uses equal sharing (into regions) and who uses their knowledge of multiplication (and division) to solve the problem. - Ensure that equipment is available and pose further problems, having students show and record their solutions in their preferred ways.
For example:
There are 16 beans in a packet. You plant 3/8 of the packet. How many beans is that?
There are 18 beans in a packet. You plant 5/9 of the packet. How many beans is that?
There are 18 beans in a packet. You plant 5/6 of the packet. How many beans is that? - Summarise finding a non-unit fraction of a set to support students to generalise the operation. Encourage explanations like “When you are finding more than a unit fraction of a set, you divide the number in the set by the denominator of the fraction. This gives you the unit fraction of the set. Then you multiply by the numerator of the fraction because this tells you how many of these equal parts are needed.”
For example: To find 3/8 of 16:
Find 1/8 first by solving 16 ÷ 8 = 2.
Find 3/8 by solving 3 x 2 = 6.
Give the answer as 6 is 3/8 x 16 = 6.
Activity 2
Have students play Telling the Truth (Copymaster 5) in pairs.
(Purpose: to identify the correct fractions of sets)
- The aim of the game is to be the player to collect the most pairs of questions with correct answers. Five cards are dealt to each player who must firstly decide which of the cards in their hand do not tell the truth. They discard these cards, turning them upside down and placing them to one side (they may need to be checked later in the game). They then find any matching pairs in their hand and place these face up in front of them.
- The players then take turns to ask for an answer card to any of the question cards in their hand, or to ask for a question card that matches an answer card in their hand.
- Upon Player One’s request for a card, if Player Two gives an untrue card, Player Two must miss a turn. Player One may immediately make another request.
- If Player Two has no suitable cards he or she tells Player One to pick up from the pile. Each time a player picks up or receives a card they must check it for accuracy.
- The player with the most correct matching pairs when all the cards are used, is the winner.
Activity 3
Conclude this session with a discussion of the game and summary of learning.
Session 6
Remind students of their learning from Activity 1 of Session 5 about finding a non-unit fraction of a set. The difference in this session is that there is no longer a predetermined number in each set.
It will be helpful to model solving a challenge with the group/class first. As students will need to find a number of cubes/tiles that can be equally split into each fraction in the challenge, a way to support students with this is to explain the following:
For the challenge ‘Build a design that is 1/3 blue and 1/4 yellow’, the number of cubes/tiles in the set has to be able to be split equally into thirds and into quarters. The simplest way to do this is to find a common multiple of the denominators involved, which in this case is 12.
Note: 12 is not the only number of cubes/tiles that could work for this challenge. In fact, any common multiple of 3 and 4 will work for this challenge.
Fraction Mosaics
You will need a bunch of cubes or square tiles in at least four colours (red, yellow, green, blue), or small square pieces of paper. The task is to build a mosaic design that matches the description in your challenge. Collaborating in pairs (mahi tahi), build your mosaic design and be ready to have a korero about it with the rest of the group/class. These mosaic designs could be combined to create a large siapo or tukutuku design, or a design for a new school garden. Links could be made with designs you have recently seen in your community (e.g. at the marae). Lay a transparent grid over an image of relevant art, and as a class come up with a list of fraction statements that describe the use of colour (e.g. 3/4 of this art uses the colour blue). This could be framed within the context of looking at how early Māori people used pigments derived from natural materials (e.g. clay deposits, iron oxide) to create paint.
Challenge list:
- Build a design that is 1/3 blue and 2/3 red
- Build a design that is 1/2 red and 1/4 green
- Build a design that is 1/5 yellow and 3/10 green
- Build a design that is 1/3 blue and 1/4 yellow
- Build a design that is 1/4 red and 1/4 blue
- Build a design that is 1/5 red, 4/10 green, and 2/5 blue
- Build a design that is 5/12 blue, 1/6 red, and 2/6 yellow
- Build a design that is 1/3 yellow, 1/6 red, and 1/2 blue
- Build a design that is 1/3 red and 1/8 green
- Build a design that is 2/3 yellow and 1/7 red
- Build a design that is 3/5 blue and 1/4 yellow
Students could create their own challenges for another pair to solve. What is the same and what is different about the way you solved it and the way another pair solved it?
Questions you could use for group korero:
- How did you get started?
- How did you decide what to do?
- How did you decide how many cubes/tiles to use?
- Is there another way to complete your challenge? How do you know?
- Can you prove that your design matches your challenge?
Dear parents and whānau,
In maths we have been learning to find fractions of sets.
Your child has brought home a game that we have been playing in class. Please return it tomorrow. You might like to write a comment about it and place the comment in the game bag. We hope you enjoy playing the game.
Here are the rules:
Telling the Truth.
(Purpose: to identify the correct fractions of sets)
The aim of the game is to be the player to collect the most pairs of questions with correct answers.
Five cards are dealt to each player who must firstly decide which of the cards in their hand do not tell the truth. They discard these cards, turning them upside down and placing them to one side. (They may need to be checked later in the game.) They then find any matching pairs in their hand and place these face up in front of them.
The players then take turns to ask for an answer card to any of the question cards in their hand, or to ask for a question card that matches an answer card in their hand. Upon Player One’s request for a card, if Player Two gives an untrue card, Player Two must miss a turn. Player One may immediately make another request.
If Player Two has no suitable cards he or she tells Player One to pick up from the pile. Each time a player picks up or receives a card they must check it for accuracy.
The player with the most correct matching pairs when all the cards are used, is the winner.