In this unit students explore the number patterns created when tins are stacked in different arrangements and keep track of the numbers involved by drawing up a table of values.
- Identify patterns in number sequences.
- Systematically “count” to establish rules for sequential patterns.
- Use rules to make predictions.
Patterns are an important part of mathematics. It is valuable to be able to recognise the relationships between things. This enhances understanding of how things are interrelated and allows us to make predictions.
Patterns also provide an introduction to algebra. The rules for simple patterns can be discovered in words and then written using more concise algebraic notation. There are two useful rules that we concentrate on here.
- The recurrence rule explains how a pattern increased. It tells us the difference between two successive terms. A pattern 5, 8, 11, 14, 17, … increases by 3 each time. Therefore, the recurrence rule says that the number at any stage in the pattern is 3 more than the previous number.
- The general rule tells us about the value of any number in the pattern. For the pattern above, the general rule is that the number connected to any term of the sequence is 2 plus 3 times the number of the term. For instance, the third number in the sequence above is 2 plus 3 x 3, which equals 11. The sixth number is 2 plus 3 x 6 = 20. To see why this general rule works it is useful to write the initial term (5) in terms of the increase (3). So 5 = 2 + 3.
It should be noted that there are many rules operating in these more complicated patterns. Encourage students to look for any relation between the numbers involved.
In this unit we ask students to construct tables so that they can keep track of the numbers in the patterns. The tables will also make it easier for the students to look for patterns.
In addition to the algebraic focus of the unit there are many opportunities to extend the students computational strategies. By encouraging the students to explain their calculating strategies we can see where the students are in terms of the Number Framework. As the numbers become larger expect the students to use a range of part-whole strategies in combination with their knowledge of the basic number facts.
This unit can be differentiated by varying the scaffolding provided or altering the difficulty of the tasks to make the learning opportunities accessible to a range of learners. For example:
- providing students with additional time to explore the patterns by drawing and counting tins, before expecting them to continue the patterns using only numbers
- working in small groups with students who need additional support, solving problems together.
The context in this unit can be adapted to recognise diversity and student interests to encourage engagement. For example:
- growing number patterns could be explored using the context of tukutuku panels in the wharenui, or the layout of seedlings for a community garden
- te reo Māori vocabulary terms such as tauira tau (number patterns), raupapa tau (number sequence), tini (tin), hokomaha (supermarket) and kapa (row) as well as numbers in te reo Māori could be introduced in this unit and used throughout other mathematical learning.
Getting Started
Today we look at the number patterns in a tower of tins (tini).
- Tell the students that today we will stack tins for a supermarket (hokomaha) display.
Show the students the arrangement:

How many tins are in this arrangement?
How many tins will be in the next row (kapa)?
Then how many tins will there be altogether?
How did you work that out?Encourage the students to share the strategy they used to work out the number of tins. “I can see 4 tins and know that you need 5 more on the bottom. 4 + 5 = 9”
“I know that 1 + 3 + 5 = 9 because 5+3= 8 and 1 more is 9.”
[These strategies illustrate the student’s knowledge of basic addition facts.]Show the students the next arrangement of tins. They can check that their predictions were correct.

How many tins will be in the next row?
Then how many tins will there be altogether?
How did you work that out?- Encourage the students to share the strategies they used to work out the number of tins.
“I know that we need to add 7 to 9 which is 16.” [knowledge of basic facts]
“I know that 7+ 9 = 16 because 7 + 10 = 17 and this is one less." [early part-whole reasoning]
“I know that we are adding on odd numbers each time. 1+3+5+7 = 16 because 7+3 is 10 + 5 + 1 = 16." Add seven tins to the arrangement and ask the same questions. As the numbers are becoming larger expect the range of strategies used to be more varied.

“16 + 9 = 25. I counted on from 16.” [advanced counting strategy]
“16 + 10 = 26 so it is one less which is 25.” [part-whole strategy]- Tell the students that the supermarket has asked for the display to be 10 rows high.
How many tins will you need altogether? - Ask the students to work in small groups to find out how many tins are needed. As the students work circulate asking:
How are you keeping track of the numbers?
Do you know how many tins will be on the bottom row? How do you know? - Gather the students back together as a class to share solutions.
- Discuss the methods that the groups have used to keep track of the number of tins.
- Work with students to make a table showing the number of rows and total number of tins. Complete the first couple of rows together.
- Ask the small groups to complete their own copy of the table on Copymaster 1. As they complete the chart ask:
Can you spot any patterns?
Write down what you notice?
Can you predict how many tins would be needed when there are 15 in the bottom row? - Encourage the students to explain their strategies for “counting” the numbers of tins.
- As a class, share the patterns noted.
Exploring
Over the next 2-3 sessions the students work with a partner to investigate the patterns in other stacking problems. Consider pairing together students with mixed mathematical abilities (tuakana/teina). We suggest the following introduction to each problem.
- Pose the problem to the class and ask the students to think about how they might solve it. In particular encourage them to think about the table of values that they would construct to keep track of the numbers.
- Share tables.
- Ask the students to work with their partner to construct and complete their own table.
Write the following questions on the board for the students to consider as they solve the problem.
How many tins are in the first row?
How many are in the second row?
By how much is the number of tins changing as the rows increase?
What patterns do you notice?
Can you predict how many tins would be needed for the bottom row if the stack was 15 rows high?
Explain the strategy you are using to count the tins to your partner?
Did you use the same strategy?
Which strategy do you find the easiest?- As the students complete the tables and solve the problem, circulate and ask them to explain the strategies that they are using to “count” the numbers of tins in the design.
- Share solutions as a class.
Problem 1:
A supermarket assistant was asked to make a display of sauce tins. The display has to be 10 rows high.
How many tins are needed altogether?
What patterns do you notice?

Problem 2:
A supermarket assistant was asked to make a display of sauce tins. The display has to be 10 rows high.
How many tins are needed altogether?
What patterns do you notice?

Problem 3:
A food demonstrator likes her products displayed using a cross pattern. The display has to be 10 products wide.
How many products are needed altogether?
What patterns do you notice?

Reflecting
In this session the students create their own “growth” pattern for others to solve.
- Display the growth patterns investigated over the previous sessions.
- Gather the students as a class and tell them that their task for the day is to invent a pattern for the supermarket to use to display objects.
- Ask the students in small groups to decide on a pattern and the way that it will grow. (A supply of counters may be helpful for some students.)
- Direct students to construct a table to keep track of their pattern (up to the 10th model). Model how to construct and use this. Alternatively, you could provide a graphic organiser for students to use.
- Once they have constructed the table ask them to record the any patterns that they spot in the numbers. Ask them also to make predictions about the 15th and 20th model.
- Direct students to swap problems with another group. When the problem has been solved, they should compare solutions with each other.
Dear parents and whānau,
In maths this week we have been looking at patterns. Patterns are an important part of mathematics. It is always valuable to be able to recognise the relationships between things to help us see how things are interrelated and allow us to make predictions.
The patterns below are to do with buildings. We have been learning about how patterns like these can be continued. An important part of this has been learning to use tables to keep track of the pattern and the relationships between terms.
Ask your child if they can continue the pattern below and say what patterns they notice in the numbers. Can they draw or fill out a table to show how the pattern would progress? Can you work out how many crosses would be in the triangle with 15 crosses along the bottom?
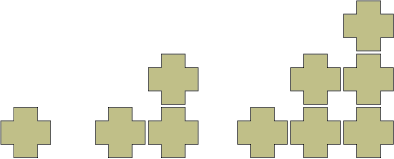
Number of crosses high | Number of crosses along bottom | Number altogether |
| 1 | 1 | 1 |
| 2 | 2 | 3 |
| 3 | 3 | 6 |