In this unit students use street maps as the context to learn about coordinates and grid references, and for giving and following instructions involving directions and distances.
- Find and describe the location of an object using coordinates and grid references.
- Follow and give directions involving turns (left and right), compass directions (N, S, E, W).
- Follow and give instructions involving distances by interpreting simple scales
In this unit students are introduced to two ways in which location is represented in real life situations, grid references and coordinates. In both cases the representation is an ordered pair, e.g. F4 as a grid reference, and (6,4) as a pair of coordinates. The convention is to state the horizontal reference (located on the x-axis) first, and the vertical reference (located on the y-axis) second.
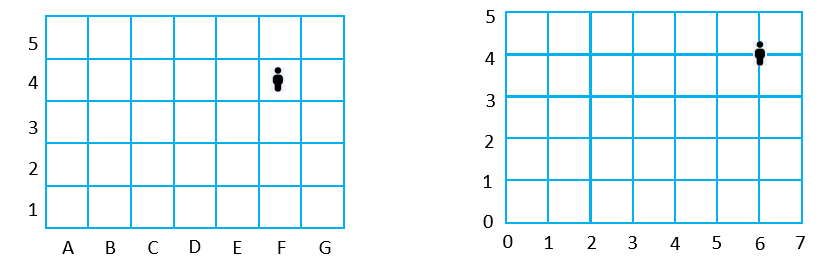
In the grid system (left image), a grid reference (F, 4) is used to locate the person in an area. Grid references are frequently used on maps. In the coordinate system (right image) the location of the person is a specific point at the intersection of the lines. The coordinate (6,4) can also be interpreted as a vector from the origin (0, 0). The vector is the combined effect of a shift of 6 units in the horizontal direction, and 4 units in the vertical direction.
The learning opportunities in this unit can be differentiated by providing or removing support to students, by varying the task requirements. Ways to support students include:
- physically acting out locations, and how to represent them, on a large-scale grid or coordinate plane
- directing students to use technology, such as Google Maps and Scratch, to experiment with representing locations, and checking to see if the coordinates are correct
- explicitly modelling use of the two systems of representations (grid and coordinate)
- discussing the similarities and differences between the two systems
- providing a wide range of hard-copy and digital maps for students to explore.
Tasks can be varied in many ways including:
- limiting the complexity of the grid or coordinate plane until the conventions of grid references and coordinates are established
- encouraging students to work collaboratively, and to check each other’s work
- using maps of locations that are familiar in the first instance, then using unknown locations to help students appreciate the significance of the representations for navigation
- provide extra practice and scaffolding for students who need support.
The contexts for this unit can be adapted to suit the interests and cultural backgrounds of your students. Using locations that are familiar and of high interest to students will support motivation. The advantage of familiar locations is that students can use their personal knowledge to validate their work. Students often view non-familiar locations through the media. For example, Great Race events are a hobby for some people, and are readily available on television. Students will enjoy a virtual Great Race through an unfamiliar part of Aotearoa. Choose locations that students show interest in, and/or hold particular cultural significance, e.g. world heritage sites that UNESCO has recognised because of the natural or cultural value. This unit offers opportunities for authentic links to be made to procedural writing.
Te reo Māori vocabulary terms such as mahere (map), ahu (direction), and huri (turn) could be introduced in this unit and used throughout other mathematical learning.
- Local street maps on grid references
- Copymaster 1
- Copymaster 2
- Copymaster 3
- String
- NZ map and index page
Session 1
- Give the students a copy of a street map of the area around the school. The map might be obtained by screen grabbing a Google Map view of the area. Ensure that you capture the scale as well. Draw a grid system on the map before you photocopy it (See Copymaster 1). Use an interactive whiteboard, screen or projector to display the map.
- Help the students to orientate themselves with the map by asking them to locate some local features. Choose places of particular significance to your students. For example, ask the students:
Where is the school on the map?
Where is the local park/sports ground?
Where is a local shop (dairy, petrol station, bakery, church etc)?
Where is your house? - Ask the students to describe the locations of the school, sports field, shop, house. Students may describe the location using street names (the dairy is on Somerville Street), other local features (the church is beside the Bushlands Park), or with directional language (e.g. north, to the left). Explain to the students that grid references are a useful way to describe locations on a map because they define what part of the map the place is in.
- Choose several examples of places on the map.
- Show the students Copymaster 1 as an introductory activity to using grid references.
How would you tell someone else where The Mole and Chicken Restaurant is located? (B3)
Where is the Taupo Hospital? (E2)
What landmark is in the grid G5 (Parts and Service)? - Ask students to work with a partner using Copymaster 1. Tell them to create eight new landmarks on the map, e.g. a dairy, a service station, a pre-school centre, a marae and Tom’s house. Ask them to make up 8 problems for another group about locating one of the landmarks. For example, What landmark is at D4? In what grid would you find Tom’s House?
- Ask groups to exchange Copymasters and solve the problems that the other group has set. Compare and self-correct the answers.
- Return to the local map on the interactive whiteboard. Suppose you were asked to create an index for your local area. The index shows the location of important landmarks. Ask your students to help by specifying four landmarks and identifying the grid reference for each landmark. Students need to record the references.
- Share the grid references by beginning the compilation of an index in alphabetical order.
- Show students an index page from an old map book which uses co-ordinate grid references. Some maps are more specific M12 NW means the location is in the northwest sector of the M12 grid.
- Discuss: Paper maps are not used much these days. Why would that be?
Mobile phone technology has made maps redundant and almost removed the need for navigational tools as well. When have you needed to use a map?
Can you imagine a place where a map might still be useful? - Remote locations often do not have GPS (Global Positioning System) signals so a paper or digital map is an important safety tool. You might look up a news story about lost and found trampers, and locate the place the trampers went missing using Google Maps.
Session 2
- Give the students a copy of the local street map from Session One. Imagine that a friend from school is coming to stay. You need to give them instructions about how to get from school to your house. Let’s imagine you live at (address, e.g. 45 Willberry Street).
- Use Google Maps to locate the address and get directions from the school.
What instructions might we give them?
Instructions must include turns (right and left), distances and important things to look for (Street names, buildings, parks, etc.) - Ask: How can we find distances on the maps?
Students may know about the scale. - Take a strip of paper and place it under the scale on the map shown on the interactive whiteboard. Mark a distance from the scale onto the strip, e.g. 200 metres.
This distance on the strip equals 200 metres in real space. Let’s tell our friend how far they need to walk along (Street name). Align the strip with the street beginning at the place where the friend starts walking. For example, “They will need to walk about 300 metres up Taharepa Road.”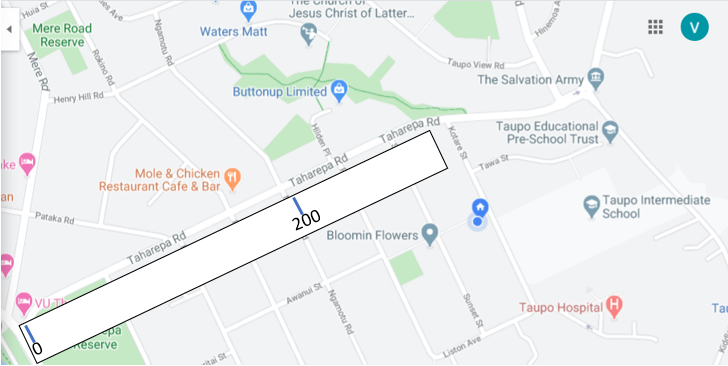
- Discuss how parts of the scale will need to be calculated to get an accurate measure. Finding fractions of the scale to get more reference marks is an excellent way to apply fractions as operators, e.g. ¾ of 200.
- Ask students to develop a set of clear instructions for their friend to walk from school to your home. Support students who have difficulty with transactional writing by introducing iconic symbols, as would appear on a navigation app for mobile phones.
- After completing a set of instructions students can trial the instructions with a partner. The partner follows the instructions exactly as recorded to see if the result matches the intended destination. Turns on maps are particularly challenging, and strategies to complete turns should be discussed. A right turn is relative to the direction of travel so the navigator needs to orientate themselves to that direction before making the turn.
Session 3
- Grid references are one way to represent a location. A3, for example, represents an area on a map so the location is not precise. That lack of precision can be problematic when an exact position is needed, e.g. courier delivery, parachute drop, police or military operation. Coordinates provide a precise location and are more associated with other ideas in mathematics than grid references.
- Show the students Copymaster 2 on the overhead projector.
What differences can you see between our grid map and this map?
Do students notice that the numbers are located on the lines rather than between those lines? - Ask: If you went to (5, 2) where would you be?
- Students learn that the first number in an ordered pair, is the horizontal distance from the origin (0, 0). The second number is the vertical distance from the origin. So (5, 2) represents five squares across and two squares up. That location is just outside the café. If the directions are reversed then students end up at (2, 5) in the forest.
- Invite the students to identify other landmarks and give the location of those landmarks using coordinates. For example:
What is at (6, 2)? (school)
What are the coordinates for the Fountain?...the Fire Station?...Ferris Wheel? - Provide students with Copymaster 2 in pairs. Ask them to:
Put ten new landmarks on the map. Label each landmark, e.g. Hospital, MacDonald’s Restaurant, Skate World, Church, Marae. Students should be encouraged to choose landmarks important to them.
Write down a set of ten coordinates for the landmarks in the order you want another team to visit them. Try to make the trip an interesting shape. - Once pairs complete their landmarks and coordinates, their map can be given to another pair to document the journey in two ways:
- Record the name of the landmark beside each coordinate
- Draw the path directly between coordinates in order to see what interesting shape is made. Name the shape.
Session 4
- Use a globe to discuss lines of longitude and latitude. Ask: Why might putting a coordinate system over the Earth’s surface be useful?
Students might think of situations where giving a precise location is important, e.g. Flights to a Pacific Island, searching for lost trampers, tracking ships, etc. - Point out that the Earth is close to a sphere, like an orange, so it is tricky to lay the lines onto a flat space. Lines of longitude emanate from the poles, and lines of latitude finish at the poles.
- Give students these names of New Zealand towns.
Ask: Do you know where these towns are in Aotearoa?- Gore 46.1028° S 168.9436° E
- Raglan 37.8° S 174.8833° E
- Dargaville 35.9333° S 173.8833° E
- Wairoa 39.0333° S 177.3667° E
- Ask: What do you think the numbers to the right of each town mean?
Students might suggest that they are coordinates. - Search for a video online using “Longitude and latitude explained.” There are some clear explanations available that students will find easy to understand.
- Go to Google Maps NZ. Put in the coordinates for each town in the search bar. Google takes you directly to the town so you can confirm its location. You may need to Zoom out so other familiar parts of Aotearoa are visible.
- Draw students’ attention to the use of decimals to more precisely define the coordinates. For example, the longitude of Wairoa is one third the distance between 177 degrees East and 178 degrees East.
- Provide your students with Copymaster 3, an old French map of Aotearoa dated at 1896. The map clearly shows lines of longitude and latitude. Ask students to mark the locations of the four towns on the old map.
- Watch to see that students:
Locate the towns using the coordinates
Use the decimals to get improved precision. - After locating the four towns ask students to use the same map and locate cities, towns, or islands that are significant to them. Exact coordinates can be found using Google Maps or sites such as https://www.geodatos.net/en/coordinates/new-zealand/.
- Students might exchange coordinates and find the matching location. You might frame the activity like a Great Race as seen on television. Each location can be a checkpoint.
Session 5
In this session students create a map that will be of future use to them. They screen grab the map from Google Maps and impose their own coordinate or grid system on it.
Using their own map students might write instructions using cardinal compass directions (N, NE, E, SE, S, SW, W, NW) and orientation instructions. In pairs the students follow each other’s instructions. The activity can be made more challenging by asking students to include an appropriate scale on the map.
Dear family and whānau,
This week we have been learning about using maps with grid references. The game Battleship is a great way to practice these mapping skills. It would be appreciated if you could take some time to play it with your child:
- If you have the game at home you can use the board game
- You can access battleship games online.
Discuss with your child places of significance in your family and locate these on a map.