This problem solving activity has an algebra focus.
Georgia starts adding up odd numbers.
She gets a surprise when she realises what pattern she is making.

What is the pattern?
Can you show why Georgia’s pattern works using counters or some other method?
- Give a general expression for the nth term of a pattern.
- Describe the links between different patterns.
- Devise and use problem solving strategies to explore situations mathematically.
This problem is about patterns, how to continue them, and how to find the general term of a pattern. Many ideas in this problem can be applied to other patterns. Finding the next term using a table and incorporating number properties are all valuable skills that can be used in many situations.
This problem the third of four related problems: Triangular Numbers, Number, Level 3; Counting Pills, Number, Level 4; and Triangular Number Links, Number and Algebra - Equations and Expressions, Level 6, in which the exploration of triangular numbers leads to an algebraic formula for the nth triangular number.
The Problem
Georgia starts adding up odd numbers. She gets a surprise when she realises what pattern she is making.
What is the pattern?
Can you show why Georgia’s pattern works using counters or some other method?
Teaching Sequence
- Introduce the problem to the class. Brainstorm ideas for approaching the problem and keeping track of what has been done.
- As the students work on the problem in pairs you might ask the following questions to extend their thinking:
What strategies might help you to find the answer?
How can you use your knowledge about numbers here?
Can you see any patterns that might help?
How can you get a general expression pattern? Using words? Using algebra? - Share the students’ answers. Ask them to explain their reasoning. Talk about what is needed to write down a complete solution to the problem.
- Ask students to write up their method of solution. Check that they have correctly used the main ideas of the argument.
- Get as many of the students to work on the Extension problem as possible.
- Discuss the extension problem with the whole class. Let them write it up at what is an appropriate level for them.
Extension
Triangular numbers are made by forming triangular patterns with counters. The 4th triangular number is 10 because it needs 10 counters.
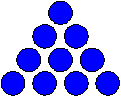
Georgia’s friend says that if you double a triangular number the answer will always be a square number. Georgia’s friend is not correct, but she is nearly correct.
How can triangular numbers be combined to make square numbers?
How can a square number be split up to give a formula for a triangular number?
Solution
In this solution we suggest some scaffolding that might help your class.
Drawing a tables is a good first strategy with a pattern problem.
term | odd number | sum so far |
1 | 1 | 1 |
2 | 3 | 4 |
3 | 5 | 9 |
4 | 7 | 16 |
5 | 9 | 25 |
6 | 11 | 36 |
Adding odd numbers seems to lead to square numbers. If we put n into the term column we should get the sum so far to be n2. (You can see too that the nth odd number is 2n – 1.)
term | odd number | sum so far |
1 | 1 | 1 |
2 | 3 | 4 |
3 | 5 | 9 |
4 | 7 | 16 |
5 | 9 | 25 |
6 | 11 | 36 |
n | 2n – 1 | n2 |
From the table we can see that 1 + 3 + … + (2n – 1) = n2.
How can we show this geometrically? Let’s have a look at an example to see if we can work it out from there. It’s always best to start small. Look at 1 + 3. To help see how things might work we’ll use different coloured counters for the different odd numbers. Somehow we have got to get the counters to make a square. There’s really only one way
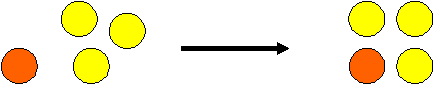
Now look at 1 + 3 + 5. We know that we have to make a square. So where can we put the 5 blue counters to make a square?
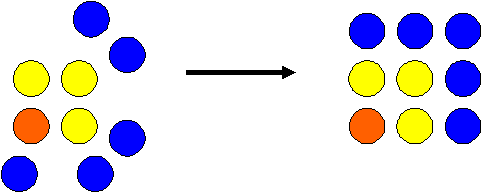
Now you can do 1 + 3 + 5 + 7 = 16 and 1 + 3 + 5 + 7 + 9 = 25 for yourselves. And can you see that it is always possible to add the next odd number around the side? You could match up 5 green counters with the blue counters in the last diagram and then there are two spaces left to put the last 2 green counters.
Another way to solve this problem is algebraically. We now realise that we have to add the numbers 1, 3, 5, …, 2n – 1. Suppose that they add up to S. We’ll write S with the numbers written forwards and backwards below.
S = 1 + 3 + 5 + … + (2n – 5) + (2n – 3) + (2n – 1).
S = (2n – 1) + (2n – 3) + (2n – 5) + … + 5 + 3 + 1.
Now add the numbers up as if they were in columns. We get
2S = [1 + (2n – 1)] + [1 + (2n – 1)] + [1 + (2n – 1)] + … + [1 + (2n – 1)] + [1 + (2n – 1)] + [1 + (2n – 1)]
= [2n] + [2n] + [2n] + … + [2n] + [2n] + [2n].
Its surprising that all of the terms add up to 2n. But how many 2n’s are there? Since there were n terms in S (we were adding together the first n odd numbers), then there must be n lots of 2n. So
2S = 2n x n = 2n2.
This means that S = n2, which is what we had been expecting.
This trick of adding things after writing them forward and backwards can be used in other situations where the difference between terms is a constant.
Solution to the Extension
This problem can be successively approached using trial and error with triangular numbers. It does not take too much of this to notice that when consecutive triangular numbers are added the answer is a square number.
This can be seen from the diagram below

So if we add the nth triangular number to the (n+1)th triangular number we get (n + 1)2. Square numbers can be divided into 2 consecutive triangular numbers in this way.
But how can we get the formula for a triangular number this from the square? Let’s do it first for a special case. Take the 4th triangular number and the 5th one (see below).

Now recolour the counters so that we emphasise the 4th triangular number (see below).

So now twice the 4th triangular number plus 5 = 52. Rearranging gives
4th triangular number = (52 – 5)/2.
Using this same argument on the nth triangular number gives
nth triangular number = [(n + 1)2 – (n + 1)]/2.
Level 5 students should probably see how this works for the specific examples (n = 5, 6, 7). It would be useful for Level 6 students to try to work through the general case. They would need to do something like this.
twice the nth triangular number plus (n + 1) = (n + 1)2, by the geometry of the situation. So
twice the nth triangular number = (n + 1)2 – (n + 1).
This gives
the nth triangular number = [(n + 1)2 – (n + 1)]/2.