This problem solving activity has a geometry focus.
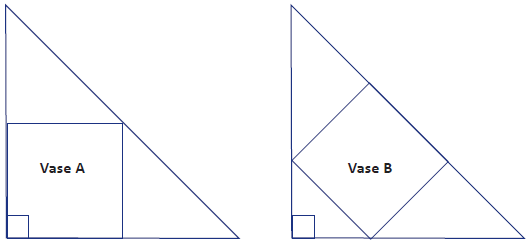
Sol is at a party and has a serviette folded into an isosceles triangle.
On the table are two square flower vases.
Although these are different sizes, they both fit on the serviette - one one way and then the other the other way.
He notices that the bigger vase A has a side length of 21cm.
What is the side length of the smaller vase?
- Use the areas of triangles and squares to find unknown lengths.
- Devise and use problem solving strategies to explore situations mathematically (be systematic, draw a diagram).
This problem involves students exploring the area of isosceles triangles and related squares.
It is possible to solve this problem using using a scale drawing. Students should be encouraged to be accurate in their drawing and to notice how the isosceles triangle can be dissected to fit into the squares in the diagram. However, it’s worth noting that, generally speaking, scale diagrams can only give approximations to the ‘real’ thing. Therefore, it is almost always necessary to do something more sophisticated to get an accurate answer. On the other hand, scale diagrams may give clues to the exact answer (see Rings and Diamonds, Geometry, Level 5) and there may be some situations where scale diagrams give sufficient accuracy for more sophisticated methods not to be worthwhile. As a general rule, only use scale diagrams when everything else has been tried.
Note: In Bill’s Badge, Measurement, Level 5 students also break up an area to enable particular information to be found.
The Problem
Sol is at a party and has a serviette folded into an isosceles triangle. On the table are two square flower vases. Although these are different sizes, they both fit on the serviette - one one way and then the other the other way.
He notices that the bigger vase A has a side length of 21cm. What is the side length of the smaller vase?
Teaching Sequence
- Introduce the problem by discussing the attributes of an isosceles triangle. Ensure students understand how to find the area of a square and an isosceles triangle, and can explain the relationship between these shapes.
- Pose the problem to the students.
- Ask the students for their initial thoughts about how they might proceed with the problem.
- Have the students work on the problem in pairs or small groups.
- If necessary, suggest that students construct the triangle or make a scale drawing of it. In the process they should more clearly see relationship between the area of the square and the area of the triangle.
- Ask the students to write their solution so that it can be shared with others in the class.
- Share solutions and discuss the similarities and differences between the approaches used.
Solution
Because the serviette is isosceles, the larger square (vase A) is ½ of the area of the triangle. Using the side length of 21cm, we can calculate the area of the triangle as 2 x (21)2 = 882 (cm2).
The other diagram can be redrawn as below.
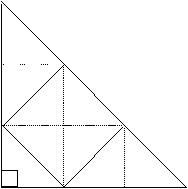
From this diagram, we can see that the triangle is made up of all 9 small triangles and the smaller square is made up of 4 small triangles. So the area of the smaller square is
4/9 x 882 = 392 cm2.
This gives the side of the smaller square as √392 = 19.80 cm.