Snazzy Snowflakes

Activity One

Question 1a is a straightforward folding and cutting task, but if students want attractive and delicate results, they will have to cut away much of the paper, and this will require care.
These snowflakes have 4 lines (axes) of symmetry because they have 3 folds. The first fold gave 1 axis, the second, 2 axes; and the third, 4 axes. If the students turn their snowflake through one complete revolution about the centre point, they will see that it appears to occupy its original position 4 times. (The students can put a dot in a corner of their snowflake to help them follow the progress of the turn.) In mathematical terms, we say that the snowflakes have rotational symmetry of order 4.
The snowflakes in question 2 are a little more difficult. When the students come to make the third fold, they have to estimate its correct position. Whether they have succeeded becomes clear with the next fold. The outer edges should meet, and the folded shape should have a symmetrical pair of points that look a bit like foxes' ears. Cutting is more difficult: there are now 12 thicknesses of paper. This time, there are 6 fold lines and the snowflake fits its original position 6 times in a complete turn, so its order of reflective symmetry is 6 and its order of rotational symmetry is 6. The same is true of real snowflakes.

To make a snowflake with 8 axes of symmetry, as in question 3a, students will need to use the same folds as for question 1 but make one further fold. They will need to start with a fairly large piece of thin paper if they are to manage the extra fold and the cutting. By now, they should be able to see that if they fold a square (through a common point), they will always get an even number of axes of symmetry. This gives them the answer to question 3b.

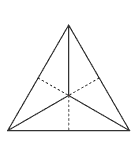
If, however, they start with an equilateral triangle (they will need to use a compass to construct one accurately), they can make a snowflake with 3 axes of symmetry. They should fold the triangle in half along the 3 lines shown in the diagram. They should then re-fold it, making valleys of the dotted lines and bringing all three vertices together. They can then cut out parts to create a snowflake with 3 axes of
symmetry and rotational symmetry of order 3.

The above folding idea could be pursued as part of question 4, and there are many other possibilities, too. The important thing is that the students are thinking about what they are doing and trying to describe the results using geometrical language.

By folding and cutting as in question 5, the students will get patterns that have two axes of symmetry and rotational symmetry of order 2. Additionally, one-half of each pattern can be translated to give the other. A pattern of this kind could be translated repeatedly to make an attractive frieze.

Activity Two

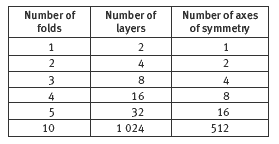
Given their previous experiences, the students may be able to complete the table in question 1 with little extra thought. If not, they will be able to establish the pattern by folding further squares with the table in mind.
When answering question 2, the students are likely to find that, at most, they can fold the square of paper 5 times. They will see from the table that 5 folds means 32 layers of paper. The folded paper is now too thick and too small (in its folded state) to allow for a further fold.

Investigation

Type "snowflake photos" in your Internet search engine to find sites that show actual snowflakes, greatly magnified. Type "paper snowflakes" into your search engine for ideas on paper snowflakes.

Answers to Activity

Activity One
1. a. Practical activity
b. 4
c. They have rotational symmetry of order 4. (The object will fit its starting position 4 times in one complete turn.)
2. a. Practical activity
b. 6
c. They have rotational symmetry of order 6.
3. a. Practical activity. Use the method in 1 but fold an extra time before cutting. Start with very thin paper, or the cutting will be difficult.
b. Not by folding and cutting a square. Each fold doubles the number of axes, so the number of axes (except the first) is always even.
4. Practical activity. Results will vary.
5. a. This design has reflective symmetry along a vertical axis and a horizontal axis and rotational symmetry of order 2.
b. Practical activity. Designs will vary.
Activity Two
1.

2. 16 axes. This involves 5 folds and 32 layers of paper. Due to the size of the folded paper and its thickness, you are unlikely to be able to fold and cut it again.
Investigation
Answers will vary.