Snap!

Problem One

Trial and improvement is one strategy that the students might use, but it is inefficient. The students will probably find the answer more quickly by working backwards:
Felicity ended up with four goats. She lost half in the third escape. So she must have had 2 x 4 = 8 before that.
Half escaped the second time, so she must have had 2 x 8 = 16 before that.
And half escaped the first time. So she must have had 2 x 16 = 32 at the start.
These results could be recorded in a table:

A double number line could also be used to solve the problem.

Four goats were left on Monday, which was one-eighth of the herd, so the starting number of goats must have been 4 x 8 = 32.

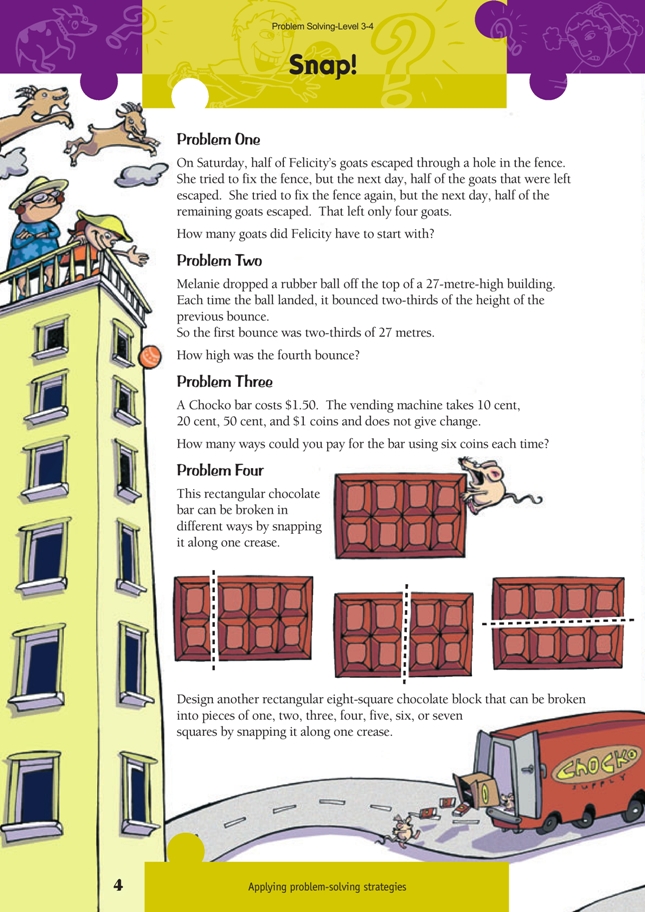
Problem Two

This problem gives the students practice in finding fractions of whole numbers (which is the same as multiplying fractions and whole numbers, for example 1/2 x 8). The problem is straightforward as long as they accurately calculate the fractions. Drawing a diagram will help them visualise the problem.

One simple way of working out the problem is:
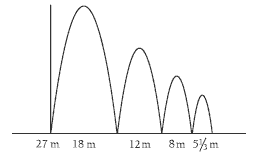
1/3 of 27 = 9, so 2/3 = 18.
1/3 of 18 = 6, so 2/3 = 12.
1/3 of 12 = 4, so 2/3 = 8.
1/3 of 8 = 2 2/3, so 2/3 = 5 1/3.
So the ball bounces to a height of 51/3 metres (5.33 metres) on the fourth bounce.
Progressive double number lines could also be used to solve this problem:

Problem Three

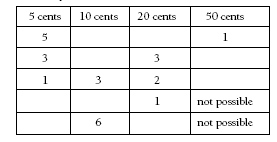
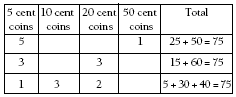
The best strategy is to build up a table, systematically starting with the largest coins and working downwards.
Using one 50 cent coin, you need five more coins to make a total of six. The only way to make the additional 25 cents with five coins is to use 5 cent coins. Working systematically in this way, there are three possible answers:

Problem Four

The students need to think about the different ways of making a rectangular, eight-square chocolate block. They will find that there are only two ways: 2 x 4 or 1 x 8 rectangles. It is not possible to get a single square by snapping a 2 x 4 block along one crease, but it is by snapping a 1 x 8 block. You can also get every other number of squares from 1 to 7 inclusive by snapping along one crease.

Hints for Students

1. Try working backwards. If that doesn’t help, try using a table and being
systematic through trial and improvement.
2. Try drawing a diagram.
3. Try using a table, being systematic, trial and improvement, or working backwards.
4. What different-shaped rectangular chocolate blocks of eight pieces could you make? Try drawing a diagram.

Answers to Problems

1. 32
2. 5 1/3 m
3. Three ways, as shown in the following table:

4. The only possible rectangular design is an 8 x 1 block.