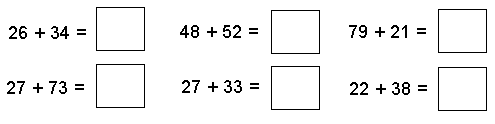In this unit students are encouraged to abandon counting methods, in favour of using known doubles facts, to derive the answers to addition problems. Using doubles is more complex but more efficient.
- Be able to recall instantly doubles from 1 + 1 to 9 + 9.
- Use known doubles facts to work out addition problems mentally using part/whole reasoning.
In this unit students are encouraged to progress from using counting on or down methods, to the use of doubles and part-whole mental methods to speed up mental computation.
Examples of counting on or counting down methods are:
- Working out 16 – 13 by starting at 13 and counting down "14, 15, 16..."; Eventually the student arrives at the answer: 3.
- Working out 29 + 4 by counting "30, 31, 32, 33"; Eventually the student arrives at the answer: 33.
Examples of more efficient part-whole methods, which draw on doubling, are:
- Working out 8 + 6 by removing 2 from the 8 to leave 6, then using 6 + 6 =12 from a known doubles fact, and then adding the removed 2 to 12 to give 14.
- Working out 26 + 25 by adding 25 + 25 to give 50 and adding 1 to give 51.
It is desirable for students to move from counting methods to part/whole methods as counting methods become too slow when working with larger and more complex numbers.
The progression from a counting method to the more abstract part/whole methods can be difficult for students. The idea of breaking numbers into suitable parts to help solve the problem is not initially obvious and may need to multiple opportunities for revisiting, modelling, and working through the strategy. For example students might model this problem on counters: Lucy has 7 orange sweets and buys 8 green sweets at the shop. How many has she got altogether?


A green sweet is removed to leave 7 in one pile and 7 in the other. Students, because they know their doubles, now say 7 + 7 = 14. Critically they must now add the removed sweet to 14 to give 15.
While this process often makes sense for students when materials are present they may experience difficulty when the materials are removed and they are asked to visualise the process. For example, to work out 9 cakes plus 8 cakes the students are asked to "see" without materials, that 9 contains 8 and 1, then to understand they use the known double 8 + 8 = 16, then they add the 1 to give 17.
The step to being able to work out addition problems by visualising is an important step along the way to being able to quickly and reliably use a "near doubles " strategy. Persistence and repeated practice is needed to help students make this transformation from needing materials to be able to image the answer.
The learning opportunities in this unit can be differentiated by providing or removing support to students and varying the task requirements. Ways to support students include:
- modelling the use of arrow cards, place value materials, and calculators
- varying the complexity of the numbers used in each activity
- providing opportunities for individual, grouped, and paired work
- strategically organising students into pairs and small groups in order to encourage peer learning, scaffolding, and extension
- working alongside individual students (or groups of students) who require further support with specific areas of knowledge or activities.
To increase the relevance of this unit, the questions posed can be adapted to reflect the interests, experiences, and cultural backgrounds of your students. You could also encourage students ready for extension to create word problems that reflect a shared, relevant context and the mathematics introduced in the session. In turn, these problems could be used as practice tasks for the rest of the class.
Te reo Māori kupu such as uara tū (place value), rearua (double), and tatau (count) could be introduced in this unit and used throughout other mathematical learning.
You could also encourage students, who speak a language other than English at home, to share the words related to counting, adding, and doubling from their home language.
- Sets of counters in two different colours
Getting Started
- Check that the students know their doubles facts before starting. If the students do not know all the facts identify which ones they do know and work from these ones.
Pose addition problems that are near doubles, that is to say the two numbers to be added are almost equal. Encourage students to solve these problems with counters, first removing or adding counters to make the piles equal, then adding or removing counters to finish the problem.
Sarah has 6 sweets and Matua has 8 sweets.
Sarah complains it is not fair because Matua has got more sweets.
Matua gives a third student some of his sweets so Sarah and Matua are now equal
How many sweets does Matua give away? (2)
How many sweets do Sarah and Matua have now? (6+6=12)
How many sweets are there altogether (12+2=14)Another strategy for solving the problem is to make Sarah’s and Matua’s piles equal (7+7=14). It usually takes time for the students to understand that Matua needs to give Sarah one sweet. The usual initial response is for the students to say that Matua should give two to Sarah.
- Pose another doubles problem. This time encourage the students to work out answers without materials by using imaging the counters or other mental processes.
Exploring
Over the next 2-4 days the students work with a partner or in a small teaching group to solve problems involving near doubles. As the students solve the problems, encourage them to share their strategies with others.
- Pose number stories for the students to solve using, for example, 6 + 7, 5 + 7, 9 + 8, 8 + 6.
- Encourage the students to use one or both of the strategies discussed on the previous day:
- Students use materials to solve them using the technique of removing some counters to make the two piles equal, using a known doubles fact, then adding back the removed counters.
- Students use materials so that each pile has the same amount.
- As the students become confident solving the problems with materials, encourage them to adjust the numbers mentally.
June has $18 and Mere has $22. Mere kindly agrees to give June some of her money so they will have equal amounts. How much money does Mere give June? How much money do they have altogether? - Increase the size of the numbers as the students become confident with making mental adjustments with the small numbers. Pose number stories that encourage students to adjust the numbers to make whole numbers of tens such as: 21 + 19, 28 + 32, 49 + 51, 23 + 27, 48 + 22, 79 + 11. (The numbers have been specially selected so that after adjusting to make the numbers equal the answer can be found by adding the relevant number of tens, e.g. 79 + 11 can be rearranged as 80 + 10, which equals 90.)
- For students that need more challenging examples, pose number stories using these numbers: 102 + 98, 97 + 303, 298 + 102, 499 + 1001
Reflecting
At the end of each session ask volunteers to explain their working and thinking to the rest of the class. You might have students create charts demonstrating how they solved a problem using a doublind strategy. These could be added to throughout the week and shared at the end of each session, before being displayed at the conclusion of the unit.
Dear families and whānau
At school this week we are using our knowledge of doubles to solve number problems. Ask your child to explain their thinking as they solve these problems.
Doubling Along
To work out 9 + 8, Marama says 8 + 8 = 16 and adds 1 to give 17.
Use Marama’s method to work out these:
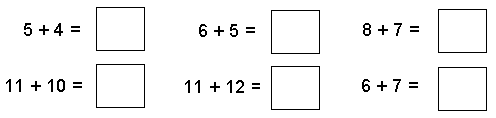
To work out 8 + 12 Ariana takes 2 away from the 12 to leave 10 and adds this 2 to the 8 to give 10. So 8 + 12 is the same as 10 + 10 = 20.
Use Ariana’s method to work out these:
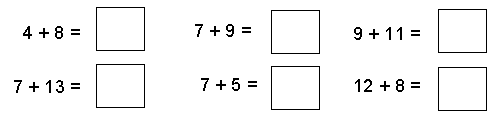
To work out 28 + 22, Lochie takes 2 away from the 22 to leave 20 and adds this 2 to the 28 to give 30. So 28 + 22 is the same as 30 + 20. So the answer is 50.
Using Lochie’s method to work out the following sums requires students to use mental strategies for addition and subtraction problems. See if you can use this strateggy to work out the answer to these problems: