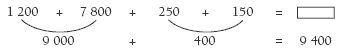Slip-sliding Away

In this activity, the students look for strategies to solve problems that involve finding a fraction of a set using simple proportions.
Use simple denominators and numerators greater than 1 to check that the students know the meaning of fractions. They should be able to explain that 2/3 means “2 out of every set of 3” in the context of a fraction of a set. 2/3 also means that 1 set is divided into 3 equal subsets, and 2 are selected. So, for a set of 6:

Use some simple examples as a warm-up mental activity, for example: 1/3 x 3 = , 1/3 x 30 =  and 2/3 x 30 = . Highlight the connections in the sequence of equations by asking: Can you use one equation to help you work out the next one?

For question 1a, the students who need to use materials could model 390 with place value materials (3 hundreds and 9 tens). They can then organise the set into thirds to find 2/3.
The students can group together two lots of the 1/3 x 390 piles to find 2/3 of 390. Encourage them to image the problem by asking them to visualise breaking up 390 into smaller numbers that are easy to break into thirds:

390 ÷ 3 = (300 ÷ 3) + (90 ÷ 3)
= 100 + 30
= 130
130 x 2 = 260
Suggestions for possible diagrams for questions 1b and 1c are given in the Answers.
Another possible diagram based on splitting 390 into 300 and 90 is:

In question 2b, check that the students can interpret the “How many 50-seater buses …” as the division equation 300 ÷ 50 =  and as  x 50 = 300. Discuss some strategies for solving these. For example: 100 ÷ 50 = 2 so 300 ÷ 50 = 2 x 3 = 6 or 300 ÷ 100 = 3 so 300 ÷ 50 = 3 x 2 = 6.
For question 3b, have the students record the equation for each cost category, for example:
20 x 60 = 
260 x 30 = 
5 x 50 = 
5 x 30 = 
Students who are using materials could use the Large Dotty Array, Numeracy Project Material Master 6-9 to cut out a rectangle to model a strategy for each equation. For 20 x 60 = , suggest that they cut out a 20 by 6 rectangle and calculate the number of dots. Ask: How can 20 x 6 = 120 help you solve 20 x 60? For 260 x 30 =  , the students could cut out a 25 by 30 rectangle and add a 1 by 30 rectangle to make 26 x 30 = 780.
Ask: How can 26 x 30 = 780 help you solve 260 x 30?
For students using number properties, there is an alternative strategy using factors that would be worth sharing with them. Ask: Can you break the numbers into easy factors to help you calculate the equations? Work with the students to get a response such as:
20 x 60 = 2 x 10 x 6 x 10
= 2 x 6 x 10 x 10
= 12 x 100
= 1 200
(This is a key idea in the transition to advanced multiplicative strategies.)
Have the students apply this strategy to 260 x 30 = :
260 x 30 = 26 x 10 x 3 x 10
= 26 x 3 x 10 x 10
= (20 x 3 + 6 x 3) x 100
= (60 + 18) x 100
= 78 x 100
= 7 800
The final addition of each cost category is another opportunity to discuss efficient addition strategies. For example:

For question 4b i, highlight the key facts:

• all 3 chairlifts have the same number of chairs

• they are full each day

• they make the same number of trips in a day.

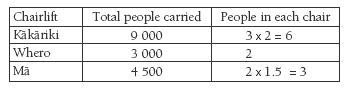
Ask: Given that these facts are the same for each lift, why do the chairlifts carry different numbers ofpeople? When the students realise that the chairs on each lift must hold different numbers, have them complete the chart for question 4b ii. One strategy may be to extend the chart to include the total number of people carried by each chair and find a relationship between them. You may need to prompt the students who find an additive relationship to look for a multiplication relationship
(for example, Whero x 1.5 = Mā; Mā x 2 = Kākāriki).

Alternatively, the students may find that Whero x 3 = Kākāriki and Kākāriki ÷ 2 = Mā. So 2 x 3 = 6 for Kākāriki, then 6 ÷ 2 = 3 for Mā.

Answers to Activities

1. a. 260
b. Diagrams will vary, but you need to focus on thirds. For example, you might use the box diagram shown on the page, or you might split the 390 into 300 and 90 and use a diagram like this:

c. Strategies will vary.
2. a. 300. (260 + 40)
b. 6 buses. (300 ÷ 50)
3. a. $2,600. (260 x 10)
b. $9,400. Strategies will vary. (You need to work out 20 x 60, 260 x 30, 5 x 50, and 5 x 30 and then add those answers together.)
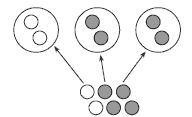
4. a. i. Kākāriki: 9 000 people; Whero: 3 000 people (9 000 ÷ 3); Mā: 4 500 people (3 000 + 1 500).
ii. 16 500 people
b. i. Answers will vary. Kākāriki’s chairs hold the most people, and Mā’s chairs
hold more people than Whero’s.
ii. Mā: 3; Kākāriki: 6. Methods will vary.
Kākāriki carries 3 times more people than Whero, so its chairs must be 3
times bigger (3 x 2 = 6). Mā carries of Kākāriki plus 1/2 of Whero, so its chairs must carry 1/3 of 6 + 1/2 of 2. 2 + 1 = 3 people on each Mā chair.