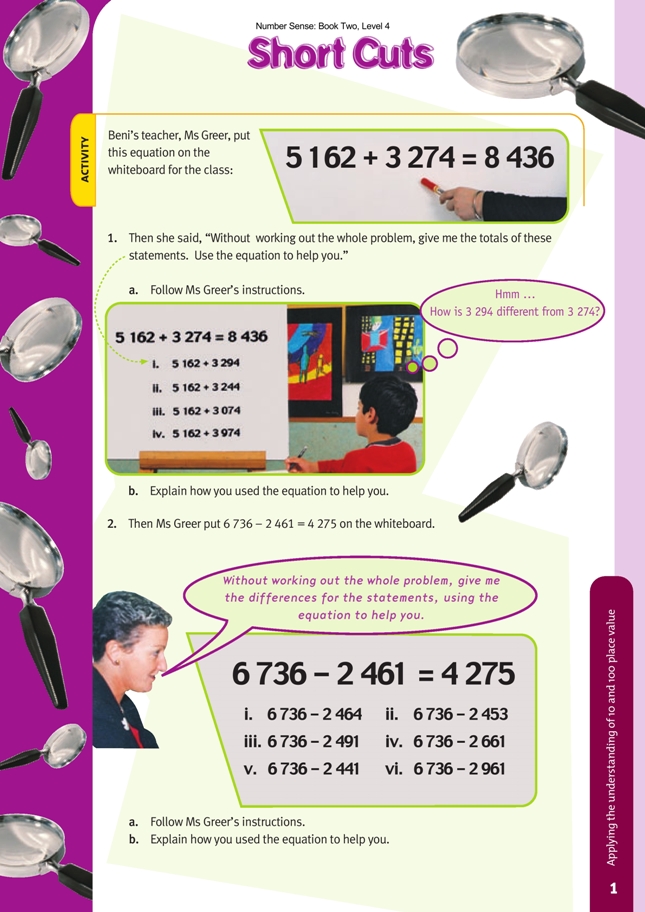
This is a level 3 number activity from the Figure It Out series. It relates to Stage 6 of the Number Framework.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (700 KB)
use place value strategies to solve addition and subtraction problems
This activity encourages the students to look for short cuts in calculations by adapting known results to solve new, but related, problems. They will need to distinguish how the new equations differ from those given on the whiteboard.
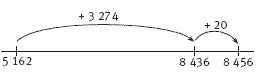
In both question 1 and question 2, the first number is the same as in the examples on the whiteboard. This means that the students have only to attend to the second number in each case. Encourage them to figure out in their heads how this differs from the second number in the whiteboard example. For the addition statements in question 1, this is reasonably straightforward. For example, in question 1a i, 3 294 is 20 more than 3 274 on the whiteboard, so the total or sum will be 20 more than 8 436, namely 8 456. Number lines can be used to help make the relationships clear. For example, in question 1a i, a possible number line is:
Note that there is no need for the line to be accurate in terms of scale because the focus is on the relationships.
The students may find question 1a iv a little trickier to do in their heads (although this is still to be encouraged). As the students solve each problem, they are expanding the number of “known” equations that they can use to compare with new problems. This means that, rather than returning to the whiteboard equation each time for comparison, they can adapt one of the solved equations to fit the particular equation that they are working on.
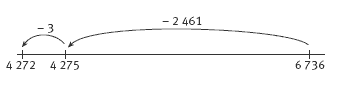
In question 2, the students are working with the idea that when we subtract one number from another, we are measuring the difference or distance between them. With question 2a i, for example, they need to realise that 2 464 is 3 more than the 2 461 on the whiteboard. The difference or result will therefore be 3 less than the 4 275 shown (because the gap between 2 464 and 6 736 is 3 less than the gap between 2 461 and 6 736). The difference or result will be 4 272. The opposite applies in question 2a ii. In this case, 2 453 is 8 less than the 2 461 on the whiteboard, so the difference will be 8 greater than the difference for 2 461.
Once again, number lines can be used to help make the relationships clear. For example, in 2a i, a possible number line is:
The last example (question 2a vi) presents a slightly greater challenge for mental calculation. 2 961 is 500 more than the 2 461 on the board, so the difference between 6 732 and 2 961 will be 500 less than for the example on the whiteboard.
Finally, having the students explain the strategies they used is important for three reasons:
1. By listening to the reasoning of others, students can learn from their peers.
2. Communicating ideas and strategies is as important in mathematics as it is in any other area.
3. From a teaching point of view, it provides an important window into the students’ mathematical thinking.
Answers to Activity
1. a. i. 8 456
ii. 8 406
iii. 8 236
iv. 9 136
b. Explanations will vary. They will probably include using the place value of 100s or 10s. For example, if the second number was 30 more, the new total would also be 30 more.
2. a. i. 4 272
ii. 4 283
iii. 4 245
iv. 4 075
v. 4 295
vi. 3 775
b. Explanations will vary. They will probably include using the place value of 100s or 10s. For example, if the second number was 30 less, the new difference would be 30 more, or vice versa (the smaller the number subtracted, the greater the difference, and vice versa).