This is a level 4 number activity from the Figure It Out series. It relates to Stage 7 of the Number Framework.
A PDF of the student activity is included.
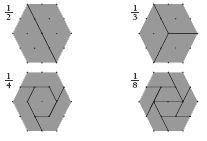
Click on the image to enlarge it. Click again to close. Download PDF (1070 KB)
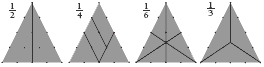
find fractions of regions within geometric shapes
Number Framework Links
Use this activity to help students consolidate and apply their knowledge of fractions
(stages 7 and 8).
FIO, Level 3+, Proportional Reasoning, Shaping Up, pages 2-3
A classmate
In question 1 of this activity, students use the properties of geometrical shapes to work out what part of their areas are white. Dots and lines give additional structure to the shapes and allow for a variety of strategies. Students must explain how they arrived at their solutions. Strategies that involve multiplication of fractions belong at stage 8 on the Number Framework; strategies based on counting belong at a lower stage.
It is important that you allow for the sharing of strategies so that students who rely on counting are exposed to other, more efficient strategies. Give your students an opportunity to do this when everyone has had a chance to solve question 1. Students need to know that any strategy that works is valid, while at the same time, they get a feel for what constitutes an efficient strategy. In this context, an efficient strategy is one that makes use of symmetry and multiplication to avoid unnecessarily counting. The extra lines on the question 1 diagrams are there to provide clues about
what some of these more efficient strategies might be.
In question 1a, students could simply count the number of smaller squares (16) that make up the large square. They could then look at the white part and see that it covers 1/2 of 4 squares, which is the same as 2 smaller squares, so 2/16 or 1/8 of the large square is white. Alternatively, they could recognise that the square has been divided in half and then in half again and again (as shown by the lines). This means that the area of the white square is 1/2 of 1/2 of 1/2 = 1/8 of the area of the large
square. Other multiplicative strategies are possible.
Question 1b can be completed in the same way as question 1a. If we count all the triangles, then the white triangle is of the large triangle. Alternatively, we can see that the large triangle has been divided into quarters and the middle quarter has been divided into quarters again, and one of those quarters is white: 1/4 of 1/4 = 1/16.
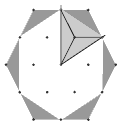
Question 1c can be broken into 12 rhombuses or 24 triangles and the white
pieces added or the red pieces added and subtracted from 1. A more efficient
strategy would be to divide the hexagon into quarters or, as in the diagram
below, sixths. The diagram shows how the sixth can be divided into 4 equal
triangles, of which 3 are white. In other words, 3/4 of the sixth is white, but
the same is also true of each of the other 5 sixths, making it true of the
hexagon as a whole.
The rectangle in question 1d has been divided into quarters, then each quarter has been divided in half and each half divided into quarters, one of which is white. This means that the area of the white triangle is 1/4 x 1/2 x 1/4 = 1/52 of the whole rectangle.
In questions 2 and 3, the students divide the shapes into equal-sized pieces and the name the parts as fractions.
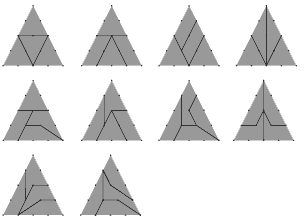
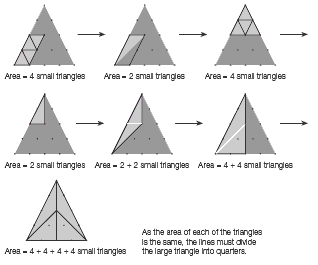
Question 4a poses a challenge that could occupy students for some time. They are likely to think that they have run out of possibilities once they have found four or five different ways of dividing the triangle into quarters, yet the question says that there are at least 10. The trick is to stop thinking of symmetrical divisions and to realise that a dot doesn’t always have to be joined to its closest neighbour. The triangle in question 4b is a further case of division into quarters. There are various
ways of showing that the areas of the four parts are equal; one is demonstrated step by step in the Answers.
Answers to Activity
1. a. 1/8. Explanations will vary. (1/2 of 1/2 of 1/2)
b. 1/16. Explanations will vary. (1/4 of 1/4)
c. 3/4. Explanations will vary. ( 18/24, using triangle units)
d. 1/32. Explanations will vary. (1/4 of 1/2 of 1/4 )
2. Answers will vary. Here are four:
3. Answers will vary. Here are four:
4. a. Here are 10 distinct ways:
b. Yes, the lines do divide the triangle into quarters. Here is one way of showing this: