In this unit students make and investigate a variety of three dimensional shapes. By examining a wide range of shapes and looking at the relationship between the numbers of faces, edges and vertices they see whether they can “discover” Euler’s famous formula.
- Construct models of polyhedra using everyday materials.
- Use the terms faces, edges and vertices to describe models of polyhedra.
A polygon is a two-dimensional shape with straight sides. A polyhedron is a fully enclosed three-dimensional object with faces that are polygons. A Platonic solid is a special type of polyhedron, made of identical, regular (all angles equal and all sides equal), polygonal faces with the same number of faces meeting at each vertex. The Platonic solids were named after the Greek mathematician Plato (though actually proved by Euclid).
There are 5 Platonic solids, the tetrahedron (4 triangles, 3 meeting at each vertex), the cube (6 squares, 3 meeting at each vertex), the octahedron (8 triangles, 4 meeting at each vertex), the dodecahedron (12 pentagons, 3 meeting at each vertex), and the icosahedron (20 triangles, 5 meeting at each vertex).

Terms commonly used to describe the attributes of polyhedra include:
- Face: A single polygon in a solid figure
- Edge: A line where two faces connect
- Vertex: A point of intersection of edges – a corner
In the 1750’s Leonhard Euler discovered a famous relationship between these three properties. The number of vertices, plus the number of faces take away two equals the number of edges.
E = V + F - 2
For a more detailed and comprehensive unit that covers the Platonic solids and extends the ideas further, see Polyhedra (3D shapes).
The learning activities in this unit can be differentiated by varying the scaffolding provided or altering the difficulty of the tasks to make the learning opportunities accessible to a range of learners. Ways to support students include:
- providing pre-made versions of models for students to refer to
- providing nets for students to construct models with
- restricting the number of models that students are asked to make
- using digital tools to construct and display shapes, and record ideas from class discussion
- working with small groups of students to support them in building models
- pairing and grouping students to support or extend their learning (tuakana-teina).
This unit is focussed on the construction of specific geometric shapes and as such is not set in a real world context. There are ways that it could be adapted to appeal to the interests and experiences of your students. For example, students could be given the opportunity to decorate a model of their favourite Platonic solid in a style of their choice for a class display. This could make reference to cultural motifs, patterns, colours, and images that are relevant to your students, or those featured in an artist study. Groups of students could also be asked to transform a selection of platonic solids into an object (e.g. a robot, a futuristic city, a new school - consider how links could be made to your current context of learning and your students’ interests).
Te reo Māori vocabulary terms such as āhua (shape), tapa (edge), mata (face of a solid figure), ahu-3 (3 dimensions) and the names for individual shapes could be introduced in this unit and used throughout other mathematical learning. Students might be engaged in looking at how the te reo Māori kupu for shapes describe the form of a shape (i.e tapatoru - triangle. Tapa means edge and toru means three, therefore tapatoru means ‘three sides’ and describes the form of a triangle).
- Geoblocks
- Cube models (dice or similar)
- Play-dough, blu-tack (or similar)
- Variety of polyhedra models: a polyhedron dice set is ideal if it is available
- Straws, toothpicks or pipe cleaners
- Paper and pens for recording
Getting started
- Invite the students to look at one of the cube models that you have available. Show them the materials they have to work with and ask:
Can you make a model of this shape using these materials? - Allow students time to work in pairs, or as individuals, to explore the materials and make models of cubes. Support students as necessary, helping them to create and align the faces of the shape.
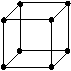
- Once most students have made a cube model successfully hold a group discussion, focusing on attributes of the shape.
What parts of this shape could we count? - Accept the terminology the students use and introduce the mathematical terms vertex, edge and face.
Construct a chart to record results for the cube. This chart will be used further as the week's investigations continue.
Polyhedron Vertices Edges Faces Cube 8 12 6 - Ask the students to make some more shapes with the materials available, making it clear that they can cut the straws to make polyhedra with shorter edges. Support students as necessary, helping them to create and align the faces of the shapes. Some of the simpler examples are shown below.
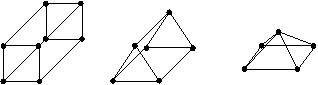
- Discuss the number of faces, edges and vertices for each polyhedron they have made.
Does anyone have one with the same numbers that looks different?
Can we see a pattern in these numbers?
Who has a polyhedron with the same number of edges? faces? vertices?
Who has a different polyhedron?
What did you discover as you made your polyhedron?
Students might recognise patterns between the attributes, or between the faces of the shapes.
Exploring
- Over the next few days have students use the materials to create a variety of polyhedra. Remember that polyhedra are composed of regular polygons (which have equal angles and equal side lengths) such as equilateral triangles, squares and regular pentagons. Students can use the geoblocks, or polyhedra dice, or digital representations, as models for the shapes they build or create their own unique examples. If you are using a dice set remove the icosahedron as this shape will be the focus for the last session of work.
- As they work, encourage students to stop and talk in pairs, considering the relationship between the number of faces, edges, and vertices.
Can anyone find a pattern with these numbers? - Explain that over 250 years ago a famous mathematician named Euler discovered there was a relationship between these numbers and challenge them to see if they can find it by the end of the week.
As a variety of shapes are made, ask students to name their shapes and introduce the mathematical terminology. Each shape has a prefix according to the number of faces it has, followed by “hedron.”
Number of faces Prefix 4
5
6
7
8
10
12tetra-
penta-
hexa-
hepta-
octa-
deca-
dodeca-- Students can use these names for their shapes or create their own. Students could also use the internet to research the names of other larger polyhedra. There is a systematic naming system and many good sites outline this. One good example is:
http://www.math.com/tables/geometry/polygons.htm#names - Throughout each session find one model to use as a focus for discussions at the end of the session. To conclude the session, count the number of faces, edges and vertices and record this on the chart. You could also add the names of these shapes in te reo Māori and other languages that are relevant to your students.
- Encourage students to look for patterns in the relationship between these three numbers.
How many faces does this shape have? How many edges? How many vertices?
Which are there the most of? Faces, edges, or vertices?
Do all the shapes have fewer faces than edges?
Do all the shapes have fewer vertices than edges?
Are there more vertices or faces in this shape? Is that the same for all the Platonic solids we’ve made?
Reflecting
- To conclude the week's investigations, show students a model of an icosahedron. If you don’t have a set of polyhedron dice containing this model you could build one using the copymaster or show a digital model.
- As you show them the model explain that they are going to predict the number of faces this shape has and then build a model to check whether they are right. Tell them the shape is made from equilateral triangles, and has 30 edges and 12 vertices. Discuss how many faces they think the shape might have, using the number of faces, edges and vertices recorded on the chart for other shapes as a guide.
Look at the other numbers on our chart.
The shape we are making has 30 edges. Do you think it will have more or less than 30 faces?
The shape we are making has 12 vertices. Do you think it will have more or less than 12 faces? - Ask students to write down their prediction of the number of faces before they construct their model. They will compare these predictions to the actual results after building an icosahedron. Hide the model as they work.
- Provide time and materials for students to build an icosahedron. To provide more structure, you could show an instructional video and direct all students, in small groups or pairs, to build their model in line with these instructions. To provide less structure, you could provide a range of materials and give students the options of following a video or looking at the model. Consider what level of structure will help your students to be most successful.
- If students have trouble building an icosahedron, remind them that the faces are made of triangles and there are five triangles meeting at each vertex and show the model as needed.
- Once students have finished building, have a class discussion to compare results:
Did you manage to build an icosahedron?
How many faces did you predict it would have?
Was your prediction correct?
How did you make your prediction? - If students haven’t identified the pattern in the numbers of faces, edges, and vertices, tell them the famous relationship discovered by Euler in the 1750s: if you add the number of vertices and faces together then take away 2, you will get the number of edges. It would be best to describe the rule in words rather than symbols at this level.
- Students check whether the famous relationship is true for all of the Platonic solids that they have recorded on the chart during the week.
- To conclude the session, have students choose and photograph their favourite model from the ones they have constructed this week, and write down what they have learnt about it. These could form a class book of polyhedra.
Dear family and whānau,
This week we have been exploring polyhedrons. Ask your child to explain how these shapes have faces, edges and vertices. For homework your child has been asked to either:
a) find photographs of different polyhedrons from magazines, junk mail or websites and create a poster page for their maths book
or
b) use materials found at home to construct an icosehedron.