This problem solving activity has an algebra focus.
Sara has some squared paper handy. She put the numbers 3, 6, 9, 12, 15, 18, 21, 24 along the top and the numbers 5, 10, 15, 20, 25, 30, 35 down the side. She then started adding the numbers together.
As she filled in the numbers she began to see patterns.
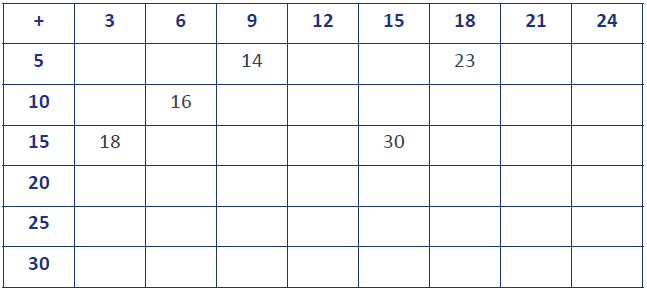
Find some patterns for yourself. Use them to complete Sara’s table.
- Describe number patterns.
- Solve problems involving patterns.
- Devise and use problem solving strategies (guess and check, make a table, look for patterns).
Patterns are an essential part of mathematics. It is important for students to start looking for them and creating them at the earliest opportunity. This problem provides students with the opportunity to look for patterns in addition. Students should be encouraged to look for number patterns in Sara’s table in the horizontal, vertical and diagonal directions.
Sara’s table is closely related to three series of problems: Magic Squares (Number), Stamps (Number), and the Table series (Algebra) which includes Jim’s Table, Level 1 and Jo’s Table, Level 2.
- Copymaster of the problem (English)
- Squared paper (or a digital grid)
- Copymaster of the problem (Māori)
The Problem
Sara has some squared paper handy. She put the numbers 3, 6, 9, 12, 15, 18, 21, 24 along the top and the numbers 5, 10, 15, 20, 25, 30, 35 down the side. She then started adding the numbers together. As she filled in the numbers she began to see patterns.
Find some patterns for yourself. Use them to complete Sara’s table.
Teaching Sequence
- Introduce the problem to the class. Ask them
What number do you think goes here?
And what about here?
Put these numbers onto the table. - Let the students work on the problem with a partner. Check that they understand what they are supposed to be doing.
- As a whole class share the students solutions. Make sure that they are looking for patterns along the diagonals and in other systematic routes through the table. Ask them to say why their pattern works.
- Encourage them to go on to try the extension problem.
- Discuss the answers that the students get in a class situation. Ask them why their answers work. Possibly ask them to make up questions of their own.
Extension
Think of Sara’s table being extended for ever in both directions.
- Which numbers are missing?
- What numbers appear only once?
- Find a number so that all other numbers after it occur in the extended table. What is the smallest such number?
- Find a number that occurs twice and so that all other numbers after it occur twice in the extended table. What is the smallest such number?
- How many times does 60 occur?
Solution
Sara’s completed table is shown below
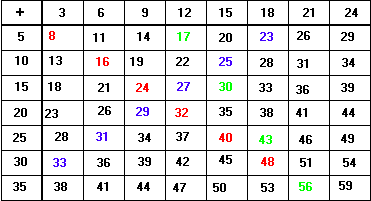
There are a large number of patterns that can be found here. The horizontal patterns are ones that increase in threes. These occur because Sara is adding 3s from her top row. The vertical patterns are ones that increase in fives. Diagonal patterns such as the one in red go up in 8s. This is because the horizontal numbers are increasing in 3s and the vertical numbers in 5s. Back diagonals (such as the one in blue) only increase in 2s. This is because there is an increase of 5 downwards but a decrease of 3 to the left. 5 – 3 = 2.
Encourage the class especially to look for patterns that occur in other ways. For instance, the ‘knight’s move line shown in green increases by 13. This is because there are two steps down (2 x 5) and one step across. 2 x 5 + 3 = 13.
Solution to the Extension
From Sara’s table, the ‘12’ column starts with 17. The "3" column has 18 in and the ‘9’ column has 19 in. Since the numbers increase in 3s going down a column, this is enough to see that every number from 17 onwards appears in Sara’s table. To find out which numbers are missing we only have to look for numbers less than 17 that don’t occur in the red box. These numbers are 1, 2, 3, 4, 5, 6, 7, 9, 10, 12, 15.
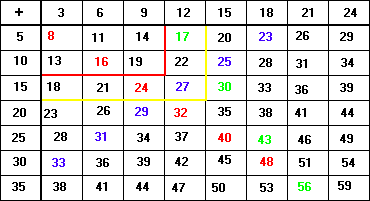
To find out which numbers only occur once, we’ll look for numbers that occur at least twice. With a little bit of help the students should see that the numbers outside the yellow box appear twice. So we only have to look at numbers inside the yellow box to find those that occur only once. All of these numbers occur only once.
Everything from 16 on appears at least once in the table. This is not so for any smaller number.
Everything from 23 on appears at least twice in the table. This is not so for any smaller number.
How would we get 60? First of all 60 could not occur to the right of the ‘60’ column nor could it occur below the ‘60’ row. So what numbers in Sara’s table will up to 60? We could go systematically across the columns but there is a neater way.
First note that 60 = 20 x 3 and since 5 x 3 = 3 x 5, we can write down the following ways of getting 60:
60 = 15 x 3 + 3 x 5;
60 = 10 x 3 + 8 x 5;
60 = 5 x 3 + 11 x 5.
So there are just three ways of getting 60 in the extended table.