The purpose of this activity is to engage students in an investigation that requires them to define the dimensions of the parameters necessary to construct a described locus.
This activity assumes the students have experience in the following areas:
- A circle is a locus of points, that are equidistant from the centre.
- Perimeter of shapes, including polygons and the circumference of circles.
- Metric units for length.
The problem is sufficiently open ended to allow the students freedom of choice in their approach. It may be scaffolded with guidance that leads to a solution, and/or the students might be given the opportunity to solve the problem independently.
The example responses at the end of the resource give an indication of the kind of response to expect from students who approach the problem in particular ways.

Work out how long each of the lengths of rope need to be to mark the track.
The following prompts illustrate how this activity can be structured around the phases of the Mathematics Investigation Cycle.
Make sense
Introduce the problem. Allow students time to read it and discuss in pairs or small groups.
- Can I imagine (visualise) and sketch what the track looks like?
- What names can I give to important features of the track?
- What information has been given?
- Is there anything missing? (The length of the straight and width of the track will need to be estimated and defined.)
- What will me answer look like? (The lengths of the ropes will be given in metres, and students will show how the measures were found.)
Plan approach
Discuss ideas about how to solve the problem. Emphasise that, in the planning phase, you want students to say how they would solve the problem, not to actually solve it.
- What are the maths skills I need to work this out? (Relationship between diameter (or radius) and circumference of a circle will be helpful.)
- What could the solution be? What is a sensible estimate?
- How could I show this problem using numbers, pictures, and calculations?
- What tools (digital or physical) could help my investigation? (Squared paper, compasses, and rulers will be helpful.)
Take action
Allow students time to work through their strategy and find a solution to the problem.
- Does my answer seem correct? Is it close to my estimation? How can I check the answer?
- How could I make sure that I haven’t missed anything?
- How do my results look different to others? Why could this be? (Other students might have a narrower or longer track. What are the implications of those differences for runners on the track?)
- Is there another possible answer or way to solve it? How does my answer compare with the dimensions of an Olympic track?
Convince yourself and others
Allow students time to check their answers and then either have them pair share with other groups or ask for volunteers to share their solution with the class.
- What is the solution?
- Can others clearly see how I worked it out?
- How do I know if I have worked this out correctly?
- Which ideas, strategies, or tools worked well in my investigation?
- How would I convince others that my findings answer the investigation question?
Examples of work
Work sample 1
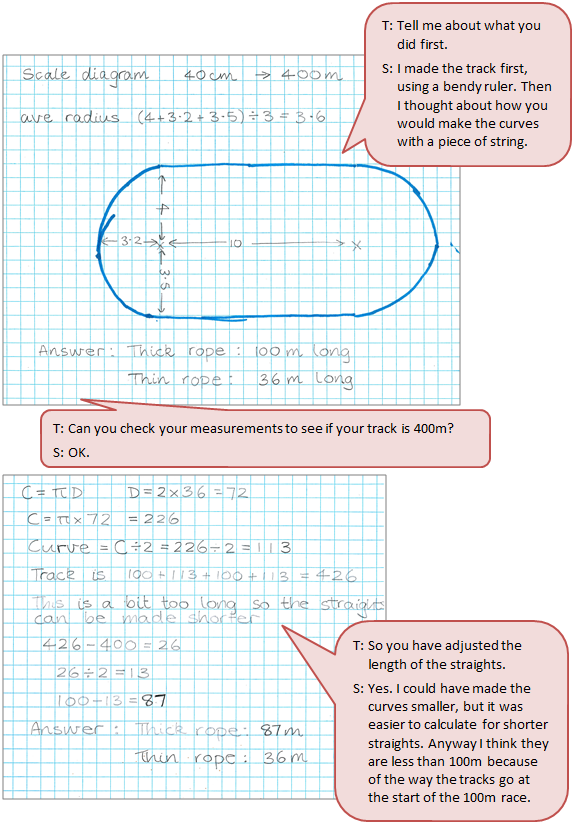
The student constructs and uses a scale diagram of the locus in order to solve the problem.
Click on the image to enlarge it. Click again to close.
Work sample 2
The student sketches the locus and calculates the parameters required to solve the problem.
Click on the image to enlarge it. Click again to close.
Work sample 3
The student sketches the locus and calculates the parameters required to solve the problem.