This is a level 3 number and measurement activity from the Figure It Out series.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (725 KB)
use multiplication to solve perimeter and area problems.
Number Framework Links
Use this activity to give students opportunities to apply multiplicative part–whole strategies (stage 6).
In this activity, students use multiplication to solve area and perimeter problems. A co-operative problem-solving approach could be used, with the students working in small groups of 3–4 and then reporting back and comparing ideas and solutions with other groups. Square Skills (page 22) complements this activity.
Discuss these key words with your students:
• Perimeter: the distance around the outside of a shape (imagine an ant walking around it).
• Area: the surface that a shape covers, measured in squares (imagine a squared blanket covering the floor).
Introduce question 1 by giving each student a geoboard and a rubber band and asking them to make a rectangle with their rubber band. Then ask:
• How many geoboard squares are there inside your rectangle?
• What’s a quick way of counting the squares that the area covers, instead of counting one by one? How could you use multiplication to make it quicker?
Expect responses such as: “I can count how many squares are along the bottom row and multiply that by the number of rows. If there are 3 rows of 4 squares, that’s 12 squares.”
For question 2, encourage the students to find a way of working out the perimeter that uses multiplication rather than simply adding the 4 sides. Expect responses such as: “I look at how many squares there are in 1 row and how many rows there are. I add those two numbers together, and then I double the total.”
When they are doing questions 3–4, the students may not realise that a square is also a rectangle and so may not include a 6 by 6 square in their list. If they haven’t encountered this idea before, have them try to define the qualities of a rectangle and then discuss with them whether a square also has these qualities. It does, so a square is a special sort of rectangle: one with all its sides the same length, just as an equilateral triangle is a special sort of triangle with all its sides the same length.
Once the students have completed their tables, ask:
• What patterns can you see in your tables? If you add each width and length, what do you notice? (They always add up to 12 with the 24-unit string and 18 for the 36-unit string. This is half of the perimeter in each case.)
• Could you use this pattern to predict all the possible combinations of length and width if you made rectangles with a 14-unit piece of string? (Each pair would add up to half of 14, which is 7. The possibilities are 1 and 6, 2 and 5, and 3 and 4.)
Extend the problem by asking Could you make a geoboard rectangle with a perimeter length that is an odd number of units? (No, because you can’t make a corner halfway between 2 nails. It would, however, be possible to draw such a rectangle.)
A key idea underpinning question 5 is that of factors. A factor is a number that is multiplied by another number to create a product. If you divide a number by one of its factors, there will be no remainder. (See also Multiples and Factors, pages 16–17.) Finding all the different rectangles that have an area of 16 squares involves using all the pairs of factors of 16: namely, 1 and 16, 2 and 8, and 4 and 4.
After the students have completed 5a and 5b, talk about factors and define them together and then ask:
• What are the factors of 16?
• How do they relate to the rectangles that you drew with an area of 16 squares?
• How could factors help us to find all possible rectangles with an area of 24 squares? (You could list all the factors and then pair them up with another factor so that each pair multiplies to make 24: namely, 1 by 24, 2 by 12, 3 by 8, and 4 by 6.)
• How could factors help us to find all possible rectangles with an area of 36 squares? (1 by 36, 2 by 18, 3 by 12, 4 by 9, and 6 by 6)
For 5c and 5d, ask: Given that these rectangles all have the same area, what do you notice about the rectangles with shorter perimeters compared with those that have longer perimeters? (They are closer to being squares. A square rectangle has the smallest perimeter for any rectangle with the same area.) This is an important and interesting mathematical idea.
Extend the problem in question 6 by getting the students to draw two more rectangles in which the one with the smallest area has the longest perimeter. (Rectangles with a shorter perimeter compared to their area will look squarer, while rectangles that are long and thin have longer perimeters compared to their area.) Interested students may like to see how far they can push this idea: “What is the greatest length the long side of the rectangle could have?” The answer introduces the important idea of a limit.
Links
Numeracy Project materials (see https://nzmaths.co.nz/numeracy-projects)
• Book 8: Teaching Number Sense and Algebraic Thinking
Squaring (relating squaring numbers to square shapes), page 28
Square Roots (using square roots to find the length of the side given the area of a square), page 29
Prime Numbers (representing prime and other numbers by arranging tiles into rectangles), page 32
• Book 9: Teaching Number through Measurement, Geometry, Algebra and Statistics Investigating Area (comparing and measuring areas), page 11
Answers
Activity
1. a. 24 squares. (4 rows of 6 squares)
b. 15 squares. (5 rows of 3 squares)
c. 18 squares. (3 rows of 6 squares)
2. a. Discussion will vary. Elsie’s likely method could be: Work out how many geoboard units “long” the two different sides are. Add those two numbers together and multiply the answer by 2.
b. Diagrams will vary. The diagram below shows how Elsie would add 3 + 4 and then double that because there are 2 sides of 3 and 2 sides of 4. (3 + 4) x 2 = 7 x 2 = 14 geoboard units long
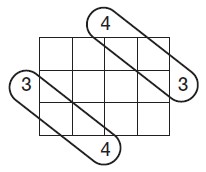
c. (4 + 6) x 2 = 10 x 2 = 20 geoboard units long
(3 + 5) x 2 = 8 x 2 = 16 geoboard units long
(3 + 6) x 2 = 9 x 2 = 18 geoboard units long
3. a. Practical activity. There are 5 different rectangles with a perimeter of 24 units possible on a 10 by 10 geoboard:
| Width | 2 | 3 | 4 | 5 | 6 |
| Length | 10 | 9 | 8 | 7 | 6 |
Note that these rectangles each have a matching rectangle. For example, a rectangle that is 3 wide and 9 long is the same as one that is 9 wide and 3 long; it’s just rotated. A square (for example, 6 by 6) is a special sort of rectangle: one with all its sides the same length.
b. Yes. A 1 by 11 rectangle would be too big for a 10 by 10 geoboard.
4.
| Width | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Length | 17 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 9 |
5. a. Practical activity. A 2 by 8 and a 4 by 4 both have an area of 16 squares and can be made on a 10 by 10 geoboard.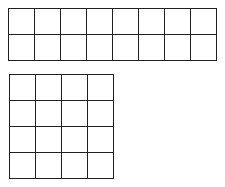
b. 1 by 16 won’t fit on a 10 x 10 geoboard.![]()
c. The 1 by 16 rectangle: its perimeter is 34 geoboard units long.
d. The 4 by 4 rectangle: its perimeter is 16 geoboard units long.
6. The 3 by 4 rectangle has an area of 12 square units and a perimeter of 14 geoboard units. There are 5 possible answers with a longer perimeter and a smaller area:
| width | length | perimeter | area |
| 1 | 7 | 16 | 7 |
| 1 | 8 | 18 | 8 |
| 1 | 9 | 20 | 9 |
| 1 | 10 | 22 | 10 |
| 1 | 11 | 24 | 11 |
Note that even though a 5 by 2 rectangle has a smaller area, it has the same perimeter as the 3 by 4. And although a 6 by 2 rectangle has a longer perimeter than a 3 by 4, it has the same area.