This is a level 5 measurement strand activity from the Figure It Out series.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (308 KB)
calculate circumference of a sphere
explore the radius and circumference relationship
calculator
computer
FIO, Level 4+, Measurement, Book Two, Round the Bend, page 17
classmate
Activity One
This activity explores how a small increase in circumference can make a surprising difference to the radius (or diameter) of a circle. The students should not attempt Round the Bend until they have had some experience of working with circles and have a feeling for the meaning of the relationship C = πd = 2πr and know how
to use the π key on their calculator.
Question 1a asks for a prediction. In fact, most people (adults as well as students) will incorrectly predict that 5 metres added to the length of a rope encircling the Earth will make a imperceptible difference. This is because they are thinking in terms of the ratio of the extended circumference to the original circumference:
if we add 5 metres to 40 000 kilometres, we are extending the circumference by only 1/8 000 000 of its original length.
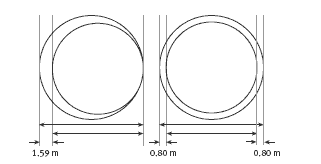
There is, however, another ratio at work here, and that is the ratio of circumference to diameter (π). This ratio tells us that, for every unit we add to the diameter, we add a little over 3 units (π) to the circumference. Working this in reverse, we can see that for every 3 units (roughly) that we add to the circumference, we add 1 unit to the diameter. So, estimating the answer to question 1b, if we increase the circumference by 5 metres, we get an increase in diameter of about 5 ÷ 3, which is about 1.5 metres. If the rope is to be suspended evenly above the spherical surface of the Earth (as the question assumes), it would stand about 0.75 metres (half of 1.5 metres) above the surface. The diagram on the following page illustrates this situation, using
the more accurate value of 1.59 metres for the increase in diameter:
The Answers give a deductive method for question 2, and it is best that the students follow this approach. But some may realise that if the rope stands 2 metres above the surface, this is equivalent to adding 4 metres to the diameter, which means that the circumference increases by 4 x π = 12.57 metres. It's that easy! (This answer, rounded to 4 significant figures, is one figure different from the given answer because there has been no need to round during the calculation.)
If the students have difficulty accepting their findings, it may help if they run string around a hula hoop laid on the tennis courts, then add a small amount of length to the string, and see how "loose" the circumference becomes.
Activity Two
This activity tells the students to use a spreadsheet formula and gives them the key information they need to do this. If they are not comfortable with the use of computers for this purpose, they are likely to lose the point of the activity because their focus will be on using the tools. There are no special difficulties involved
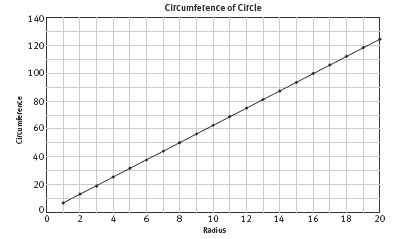
in creating the graph required for question 1iii.
You should discuss the completed graph with your students and help them understand what it means. The graph is a straight line, showing that the relationship between the radius or diameter and the circumference is linear. No matter what the radius is, if you increase it by 1 unit, the circumference increases by 2π units
(approximately 6.28 units). This is what the students should discover and describe in question 2.
Answers to Activities
Activity One
1. a. Predictions will vary. A likely prediction is that any difference will be too small to notice.
b. 0.80 m. (Circumference of Earth = 40 000 000 m, therefore radius = 40 000 000 ÷ 2π = 6 366197.72 m. Length of rope with 5 m added = 40 000 005 m,
therefore radius = 6 366 198.52. Difference in radius = 6 366 198.52 - 6 366 197.72 = 0.80 m.)
2. 12.54 m. (To be 2 m off the ground, the radius would need to be 6 366 197.72 + 2. So the length of the rope would be 6 366 199.72 x 2π = 40 000 012.54m.)
Activity Two
1. Practical activity. Your graph should look similar to this:
2. Each time you add 1 unit to the radius, the circumference increases by 2π units (approximately 6.28 units). This is true no matter how great the radius is.