This problem solving activity has a geometry focus.
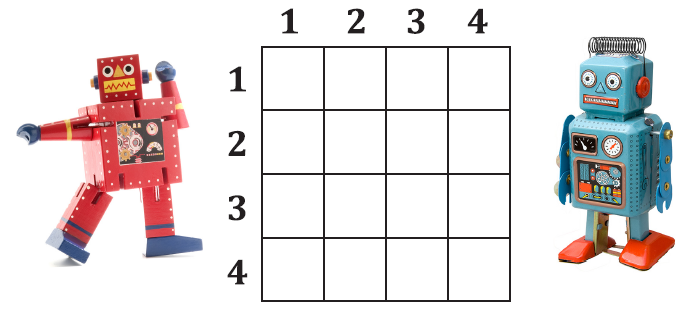
Robots can move around the 4 x 4 board below.
They can do so at the rate of one square per second.
Start the red robot at (1,1) and give it instructions (square by square) to move in a square of side length 3 around the square (2,2).
Now start the blue robot at (4,4) and write instructions for it to move in a square of side length 3 around the square (3,3).
If the red and blue robots both start at the same time from their respective corners, which squares can they both be made to occupy at the same time?
- Follow grid references.
- Devise and use problem solving strategies to explore situations mathematically (guess and check, make a drawing, use equipment).
The aim of this problem is to explore grid references and to use them in a practical situation.
- Copymaster of the problem (English)
- Copymaster of the problem (Māori)
- Counters or robots
- Grid paper
The Problem
Robots can move around the 4 x 4 board below. They can do so at the rate of one square per second.
Start the red robot at (1,1) and give it instructions (square by square) to move in a square of side length 3 around the square (2,2).
Now start the blue robot at (4,4) and write instructions for it to move in a square of side length 3 around the square (3,3).
If the red and blue robots both start at the same time from their respective corners, which squares can they both be made to occupy at the same time?
Teaching Sequence
- Introduce the 2 robots or counters and set the scene for the problem.
- Pose the problem to pairs of students.
- As the students work on the problem check that they are correctly using grid references.
What position on the grid is the robot now?
Which reference do you give first? Is it always in that order? - Share solutions.
Extension
Using a 5 x 5 grid make up your own robot problem. Write it up so that others can solve it.
Solution
There are two possible ways for the red robot to move. It could go (1,1), (1,2), (1,3), (2,3), (3,3), (3,2), (3,1), (2,1) and back to (1,1).
Similarly there are two ways for the blue robot to move. Suppose that it goes (4,4), (4,3), (4,2), (3,2), (2,2), (2,3), (2,4), (3,4) and back to (4,4). If you compare the different grid references you will see that the two robots are never on the same square at the same time.
But the blue robot might go (4,4), (3,4), (2,4), (2,3), (2,2), (3,2), (4,2), (4,3) and back to (4,4). In this case the two robots are on the same square at the same time twice – the squares (2,3) and (3,2).
If the red robot goes round its square the other way (anti-clockwise) it will meet up twice with the blue robot if the blue robot goes clockwise. Then they meet on the squares (3,2) and (2,3). If the blue robot insists on going anticlockwise, then they won’t meet up at all.
So the two robots can be made to simultaneously occupy the squares (2,3) and (3,2).