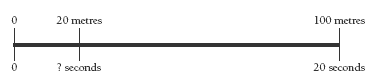This is a level 3 number, measurement and geometry activity from the Figure It Out theme series.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (629 KB)
multiply by multiples of 10
estimate using scale factors
order weights
calculate speeds
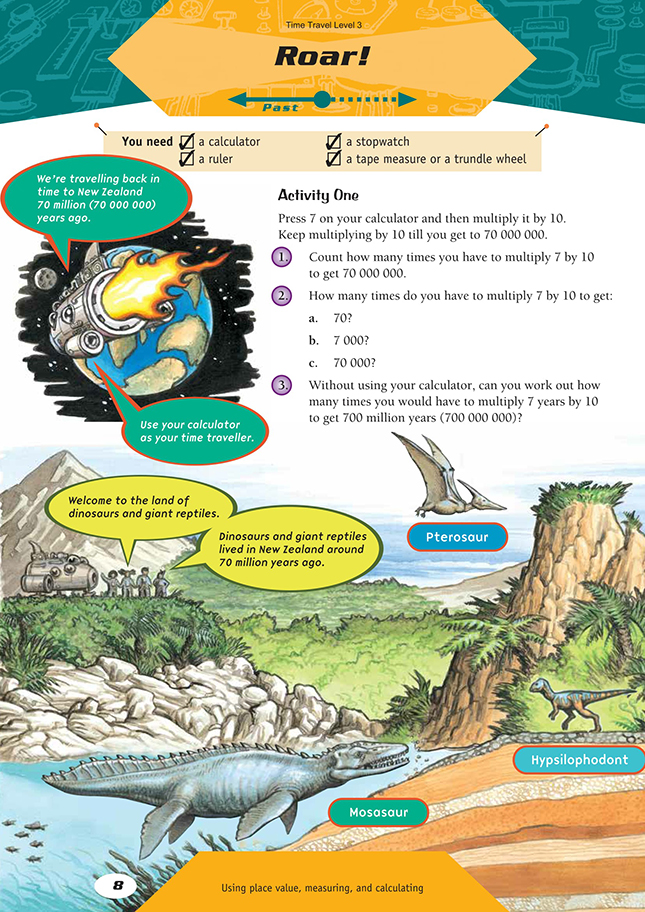
FIO, Level 3, Theme: Time Travel, Roar! pages 8-9
A calculator, a ruler
A stopwatch
A tape measure of a trundle wheel
Activity One
This activity explores the link between place value and multiplying a number by 10, which is a key idea in developing an understanding of place value.
The students could use the constant function on their calculators for this activity. To set up multiplying by 10 as a constant function, they will have to press the 10 x 7 and then the = sign as many times as they want to multiply by 10. (Some calculators may require the x key to be pressed twice, that is, 10 x x 7 = .)
Page 16 of Answers and Teachers’ Notes: Number, Figure It Out, Level 3, discusses concepts relevant to this page, that is, multiplying and dividing by 10 and understanding place value.
This activity can be extended by investigating what happens when you press 70 000 000 into the calculator and divide by 10. “How many times do you have to press the = key to get to 7? What happens if you press the = key 10 times?”
Activity Two
This activity helps to develop estimation and measuring skills. The students also need to use scale to calculate lengths and to order decimal numbers.
Students need practice at estimating measurements. Using an item with a known length, for example, a table top, ask the students to estimate the length of the whiteboard, the width of the room, and other items in the classroom. They can then check their estimates. (See also Measurement, Figure It Out, Levels 2–3, pages 1 and 3.)
When the students are measuring the Pterosaur, make sure that they measure its length, from the tip of its beak to the end of its tail, and not its wingspan.
Converting the measurements from centimetres to metres is fairly straightforward because the scale is 1 centimetre : 1 metre, so students only need to change the units of their measurements.
The following books contain some interesting information about New Zealand dinosaurs:
Hayward, B. (1998). Trilobites, Dinosaurs, and Moa Bones: The Story of New Zealand Fossils. Auckland: Bush Press.
Long, J.A. (1998). The Dinosaurs of Australia and New Zealand and Other Animals of the Mesozoic Era. Sydney: UNSW Press.
Stevens, G., McGlone, M., and McCulloch, B. (1998). Prehistoric New Zealand. Auckland: Heinemann Reed.
Wiffen, J. (1998). Valley of the Dragons: The Story of New Zealand’s Dinosaur Woman. Glenfield, New Zealand: Random Century, 1991.
Investigation
Discuss the idea of speed with the students. They should all be familiar with the speed of cars and speed limits. Talk about the term “kilometres per hour” as a common measure of speed and also introduce the term “metres per second”. You could perhaps compare the speed of 100 metre sprinters with 1 500 metre runners. The students could calculate the speeds in metres per second at which these distances are run and discuss why the speeds are so different.
Discuss with the students how they could calculate how long the theropod would take to run 20 metres. A diagram or double number line might help the students to work through this problem, for example:
Scientists can estimate a dinosaur’s speed from a formula that has been developed that involves calculating leg and stride length (Alexander, R.M. [1976]. “Estimates of Speeds of Dinosaurs”. Nature, no. 261, pp. 129–130). The students could measure their own stride and leg length and see if there is a correlation with their own velocity.
Answers to Activities
Activity One
1. 7 times
2. a. once
b. 3 times
c. 4 times
3. 8 times
Activity Two
1. Estimates will vary but should be approximately 7 m for the theropod, 12 m for the mosasaur, and 3 m for the pterosaur.
2. Theropod – 7 m
Mosasaur – 12 m
Pterosaur – 3 m
3. a. Pterosaur
b. So it can fly
4. Answers will vary. Examples are elephants, hippopotamuses, and whales.
Investigation
1.–3. Practical activities
4. 4 seconds
5. Practical activity
6. No.