The purpose of this activity is to engage students in calculating a combined probability and using this to solve a problem.
This activity assumes the students have experience in the following areas:
- Estimate the probability of events by experiment.
- Create theoretical models of probability by finding all the possible outcomes.
- Reasoning with proportions and expressing proportions using fractions, decimals, and percentages.
- Combining probabilities for independent events.
The problem is sufficiently open ended to allow the students freedom of choice in their approach. It may be scaffolded with guidance that leads to a solution, and/or the students might be given the opportunity to solve the problem independently.
The example responses at the end of the resource give an indication of the kind of response to expect from students who approach the problem in particular ways.

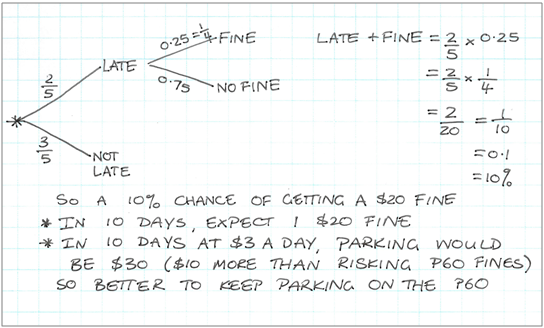
Task: Janice has an after school job, for an hour each school day. To get to the job, she parks her moped on a P60 space on the street outside. She doesn't use the nearby parking building which charges $3 for the first two hours of parking.
Using the P60 is usually fine, but she does get held up at work 2 out of every 5 days and so overstays the allowed 60 minutes on those days. There is a 25% chance on any given day, that parking wardens are around and will write a $20 fine for cars overstaying their park.
Should Janice keep risking the P60 parking, or would she save money by using the parking building?
The following prompts illustrate how this activity can be structured around the phases of the Statistical Enquiry Cycle.
Problem
The problem section is about what data to collect and who to collect it from and why it’s important.
- What is my investigation question? (Students need to be clear that the purpose of the investigation is to estimate or calculate the cost of risking a fine and compare that cost to that of parking in the building.)
- Do I have all the information I need, or is some missing?
- Have I investigated a similar problem? What strategies did I use then?
- Will I be better to conduct an experiment or work the probability and cost theoretically?
Plan
The planning section is about how students will gather the data.
- How will I go about answering this question? (Student might choose to experiment or work the problem out theoretically.)
- What will I need to know? (The cost of risking fines.)
- What number of days should I find the costs for? Why choose that many days?
- How will I organise an experiment to estimate the chances of getting a fine over a given number of days?
- What tools will I need to ensure my experiment is random and not biased?
- Is there a way to calculate the probability? What models will be useful to do that? (Students should be able to use a tree diagram to find the probability of getting a fine over a given number of days.)
- Can I predict possible answers to my question, even before I look at experimental data or a model of all outcomes? Which option do I expect to be cheaper?
Data
The data section is concerned with how the data is managed and organised.
- What tools will I use to generate random outcomes that match the probability of 1 in 10? (Random number generators or the Sampler plugin from CODAP might be used.)
- How many trials should I do? Why should I do that many? (Look for recognition of the greater reliability of experimental results involving larger samples.)
- How will I record the data I get so I can interpret it? (Trials of 5 ‘cookies’ collated in a table or spreadsheet with 5 columns will make analysis easier.)
- What digital or written tools will help my organise my data? (Consider software including spreadsheets.)
Analysis
The analysis section is about exploring the data and reasoning with it.
- Have I reflected back on my question so I am clear what I am trying to find out?
- What tools display the data from my experiment in an efficient way? What do the results show?
- How can I express my results as an estimate of the probability of getting a fine?
- How does that estimate align with the theoretical probability I calculated?
- Can I make preliminary statements about my findings, starting with “I noticed that...”
Conclusion
The conclusion section is about answering the question in the problem section and providing reasons based on their analysis.
- Have I answered my original question? If not, why not?
- How might I convince someone else I have answered the question? (Both experimental results or theoretical models or both can be used.)
- Do my experimental results align with my theoretical model? If not, why not?
- Is my summary of findings clearly written so others can understand it?
- What strategies and tools proved the most useful in my inquiry?
- What other things have I learned and what further questions do I have?
- How would these results alter if parking wardens came more frequently or the fines were increased?
Examples of work
Work sample 1
The student calculates a combined probability and use this to solve a problem, with guidance.
Click on the image to enlarge it. Click again to close.
Work sample 2
The student calculates a combined probability and use this to solve a problem.