This is a level 5 measurement strand activity from the Figure It Out series.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (481 KB)
find the perimeter (cicumference) of a circle
find the area of a circle
FIO, Level 4+, Measurement, Book Two, On the Right Track, pages 18 -19
drawing compass
calculator
narrow strip of card
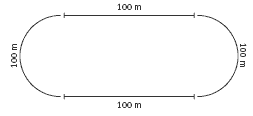
This activity features an annual school event that has considerable mathematical potential, the marking out of the athletics track. In practice, the groundsperson or the caretaker usually does this using string, pegs, and a long tape and follows a process that gives a correct result without much calculation. In this activity, the students have to use their understanding of the π relationship to answer questions and draw scale
diagrams of the oval track and an alternative circular track.
The students should not find questions 1 and 2 difficult as long as they realise that each of the 4 sections of the inside track (2 straights and 2 semicircles) are exactly 100 metres long. (See the illustration in the Answers.) They will have a problem with question 3b if they don't notice that the width of the lanes is given in centimetres rather than metres. Note that they are not asked to draw in all the individual lanes on the scale diagram. This is because the scale they are using is too small.
In question 4, the students may be tempted to use the outer edge of lane 8, as constructed in question 3, but runners do not use the outer edge because they know that the distance around the inner edge is less. Students who have worked through and understood the previous activity, Round the Bend (page 17 of the students' book), may realise that, as the diameter of the inside of lane 8 is 2 x 5.25 = 10.5 metres greater than the inside of lane 1, the extra length involved can be simply calculated in this way: 10.5 x π = 33.0 metres (rounded to 3 significant figures). (7 lanes each 0.75 metres wide give a total width of 7 x 0.75 = 5.25 metres.)
Although the students could calculate the answers to question 5 using proportion and a protractor, you should suggest that they use string or a thin strip of card to mark the curved distances.
In question 6, they find the area of the rectangle and circle and add them together. In question 7, they find the diameter of the circle and then use it to calculate the area. They can compare the two areas in a number of ways, but however they do it, encourage them to express their comparison in suitably rounded numbers.
In questions 8 and 9, the students apply processes similar to those used in questions 3-5, this time to a circular track.
If the students are doing this activity prior to their own school athletics track being marked, they may be able to help the caretaker set out the marker pegs for each lane or they may be able to set the markers out themselves and have the caretaker check them before painting in the start lines.
Note that, in most cases, the students need to round their answers when working through this activity. Because the degree or method of rounding is not specified, they may end up with answers that are a little different from those in the Answers. If they get different answers, don't assume that rounding is the reason. And don't inadvertently give the impression that as long as their answers are somewhere in the ballpark, this is good enough. Many students struggle to understand the meaning and value of rounding and need a lot of careful coaching.
Cross curricular links
Physical Education and Health
This activity could be part of a unit based around running, jumping, and throwing.
Achievement Objectives
- acquire and apply complex motor skills by using basic principles of motor learning (Movement Concepts and Motor Skills, level 5)
- investigate and practise safety procedures and strategies to minimise risk and to manage risk situations (Personal Health and Physical Development, level 5)
Answers to Activity
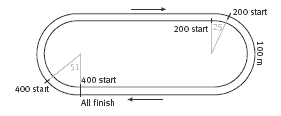
1. 100 m. See the diagram:
2. 63.66 m. (200 ÷ π)
3. a -b. Practical activities
4. a. 432.98 m. (200 + 74.16 x π )
b. 33.0 m. (433.0 - 400)
5. Practical activity. In the 200 m event, the runner in the inside lane would start at the point where the first curve and the second straight meet; the runner in the outside lane would start 16.5 curved metres in front of this. In the 400 m event, the runner in
the inside lane would start on the finishing line; the runner in the outside lane would start 33.0 curved metres in front of this.
6. 9 549 m2 (slightly less than a hectare).
(Area of rectangle + area of circle = 100 x 63.66 + π x 31.832
= 6 366 + 3 183 = 9 549)
7. a. Yes. The diameter of a circle with a circumference of 400 m is 127.3 m. (400 ÷ π). Its radius is 127.3 ÷ 2 = 63.65. Its area = π x 63.652 = 12 728 m2, which is greater than the 9 549 m2 for the other track.
b. Possible comparisons include:
- The area of the circle is about 1/3 (33%) greater than the area of the oval (12 728 ÷ 9 549 = 1.33 = 133%)
- The area of the oval is about 3/4 (75%) of the area of the circle (9 549/12 728 = 0.75 = 75%)
- he ratio of the area of the circle to the oval is approximately 4:3.
8. a. Practical activity
b. 437.7 m. (The diameter of the outside track of the circle is 127.32 + 12 = 139.32 m. The circumference is therefore π x 139.32 = 437.7 m.)
9. The starting positions will be 16.5 and 33.0 curved metres ahead of the positions for the runner in the inside lane.