The purpose of this activity is to engage students in applying transformations to create repeating tiling patterns.
This activity assumes the students have experience in the following areas:
- Applying transformations (translations, reflections, rotations) to create designs.
- Calculating the effect of enlargement by a scale factor on side length and area of the image.
- Recognising the properties of similar shapes.
The problem is sufficiently open ended to allow the students freedom of choice in their approach. It may be scaffolded with guidance that leads to a solution, and/or the students might be given the opportunity to solve the problem independently.
The example responses at the end of the resource give an indication of the kind of response to expect from students who approach the problem in particular ways.
Reptiles are shapes that tile to make a larger version of themselves. Here is an example, a trapezium. Notice how the whole is made up of four identical parts.
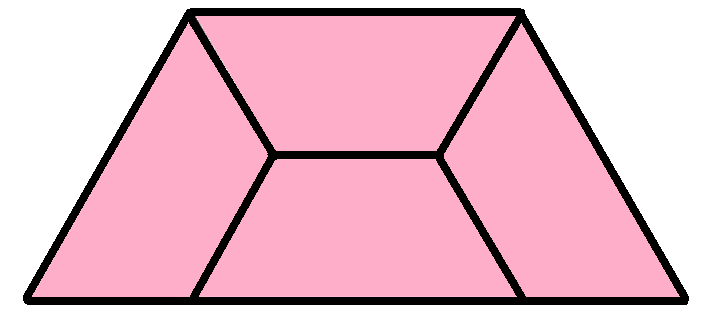
What transformations (translations, reflections, rotations) map the top trapezium onto the other three?
How might 16 copies of the shape tile to form an even larger copy of itself?
Here are some other reptiles. Four copies of each shape will tile to form a larger copy of itself. Figure out which transformations are needed.

Notice that these shapes are Rep-4 because you need four copies to make a larger whole of the same shape.
Can you find some other Rep-4 shapes?
The following prompts illustrate how this activity can be structured around the phases of the Mathematics Investigation Cycle.
Make sense
Introduce the problem. Allow students time to read it and discuss in pairs or small groups.
- Do I understand the situation and the words? (Students may need support to understand the properties of a reptile shape, starting with Rep-4.)
- What properties of the Rep-4 image and the original tile are the same. (Students need to recognise that the invariant properties of shapes under enlargement apply. Those properties include equal angles, and effect on side length and area.)
- Does this look/sound like a problem I have worked on before? (Students may connect to other geometric puzzles such as tessellations.)
- Where else in my life/the world can I see this happen?
- What will my solution look like? (The solution will be a selection of shapes classified as reptiles and non-reptiles, with some indication of why reptiles work.)
Plan approach
Discuss ideas about how to solve the problem. Emphasise that, in the planning phase, you want students to say how they would solve the problem, not to actually solve it.
- What would be a good first move? (Students might elect to begin with simple shapes they know will work, such as triangles and squares.)
- If I have the original tile, how might I draw the outline of what the Rep-4 looks like?
- If I have the outline of the Rep-4, what strategies might I use to see if the original shape fits into it? (Making copies of the original shape that are movable might help.)
- What geometric transformations can I try on the original shape?
- What tools (digital or physical) could help my investigation? (Digital platforms such as Geogebra or PowerPoint can make manipulation of the original shapes easier.)
Take action
Allow students time to work through their strategy and find a solution to the problem.
- Have I worked in a systematic way, starting with simple original shapes, and progressing to more complicated shapes?
- Have I classified the shapes that are reptiles and those shapes that are not?
- Is there anything in common with reptile shapes?
- Is there anything the same about the transformations the fit the original shape into the Rep-4 shape?
- Do my solutions make sense and answer the question?
- Can I see and describe a generalisation about reptiles and how they fit together to form Rep-4s?
Convince yourself and others
Allow students time to check their answers and then either have them pair share with other groups or ask for volunteers to share their solution with the class.
- Have I considered a lot of different cases (shapes)?
- What is the solution? Does it describe the properties of reptiles?
- Does my solution describe the transformations that are used? Is there anything the same about the way the reptiles fit together?
- Have I explained why some shapes are not reptiles?
- Is my working clear for someone else to follow?
- How would I convince someone else I am correct?
- Could I have solved the problem in a more efficient way?
- Is there some mathematics that I would like to learn?
Examples of work
Work sample 1
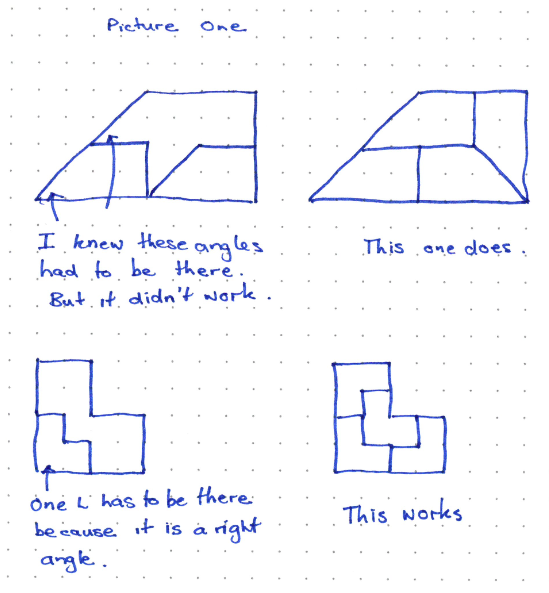
The student uses trial and error approaches with some acknowledgement of angles and side lengths to tile the shapes.
The examples of Rep-4 shapes are simple enough that the tiling can be found by trial and error. However, the time a student takes to find the arrangement is greatly reduced if they attend to congruent angles. Students may produce cut-outs of the shapes and manipulate them to find the arrangement. Alternatively, they may draw large copies of the shape and subdivide it into four identical shapes. Square and triangular dot paper is useful.
Below the student looks for congruent angles and combines that approach with trial and error.
Click on the image to enlarge it. Click again to close.
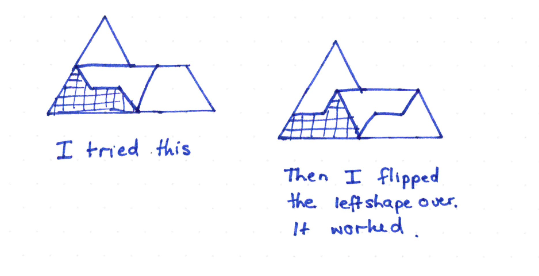
The mountain reptile is harder to solve as there are two possible orientations for the starting shape.
Click on the image to enlarge it. Click again to close.
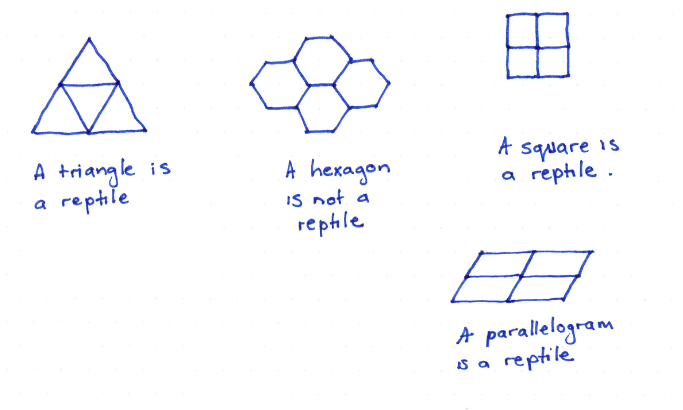
Students using a trial and error approach are likely to find some simple Rep-4 shapes, such as the square, equilateral triangle and parallelogram.
Click on the image to enlarge it. Click again to close.
Work sample 2
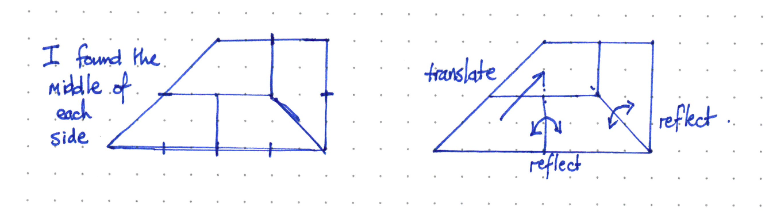
The student applies the properties of transformations, including enlargement, to find how four copies of the shape form a larger version of itself.
The first important principle to notice about Rep-4 shapes is that the side length of the larger shape is twice that of the smaller shape. If side length is doubled then the area of the resulting shape is 2 x 2 = 4 of the initial shape.
Students who attend to this property of enlargement, and look for congruent angles, are likely to solve the puzzles more easily. They will also notice the transformations that map one shape onto the adjacent one.
Click on the image to enlarge it. Click again to close.
Creation of ‘new’ reptiles is also easier if students look at the transformations that occur with the given examples.
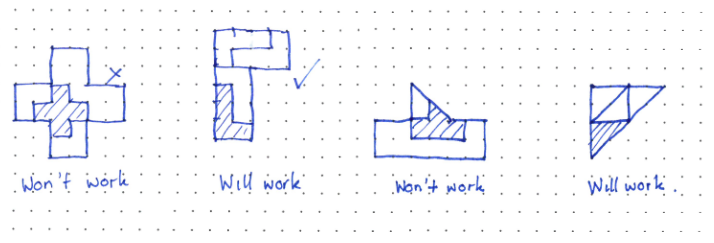
To test a shape for reptilian tendencies it seems that translation is the easiest transformation to attempt first. If that does not work, then try other possible transformations like reflection and rotation. Even so, non-reptiles are much easier to find than reptiles. Suggest to students that they start with shapes composed of squares and equilateral triangles. Simple shapes are more readily tiled than complex shapes. Here are some examples:
Click on the image to enlarge it. Click again to close.