New Zealand Curriculum: Levels 4
Learning Progression Frameworks: Multiplicative Thinking, Signpost 6 to Signpost 8
Target students
These activities are intended for students who use a range of strategies for addition, subtraction, and multiplication of whole numbers. They should have knowledge of many basic facts for addition, subtraction, and multiplication.
The following diagnostic questions indicate students’ understanding of rates and how to find unknown values in a rate problem. Students must come to understand that both ‘between’ and ‘within’ measure strategies are valid and should develop their capacity for finding the multiplicative operator that connects measures. Allow access to pencil and paper. A calculator can be used to check answers if needed. (show diagnostic questions)
The questions should be presented orally and in a written form so that the student can refer to them. The questions have been posed using a square tiles context but can be changed to other contexts that are engaging to your students, such as tukutuku panels or tapa cloth.
- Potatoes cost $3.00 per kilogram. How much do you pay for a 5-kilogram bag of potatoes?
Note: This is a problem in which the unit rate is given, and the amounts are whole numbers.
Signs of fluency and understanding:
Uses the multiplication fact 5 x 3 = 15 to calculate that the cost is $15.00. The student coordinates the two measures, weight in kilograms and cost/price in dollars and gives the answer in appropriate units. This indicates some understanding of “per” meaning “for every.”
What to notice if they don’t solve the problem fluently:
Unsure about what to do with the numbers, five and three, and may speculate that the answer is eight (5 + 3) or two (5 – 3). This may indicate that the student needs further opportunities to solve simple problems with rates. This might initially make use of objects or diagrammatic representations.
Calculates 5 x 3 = 15 using repeated addition, i.e., 3 + 3 + 3 + 3 + 3 = 15 or skip counting, i.e., “3, 6, 9, 12, 15.” This indicates that the student needs to develop fluency with single digit multiplication. Look for understanding of rates and the correct use of units, dollars in this case.
Supporting activity:
Unit rates
- You pay $20 for 5 kilograms of oranges. What is the price of oranges?
Signs of fluency and understanding:
Divides 20 ÷ 5 = 4 and names the answer correctly as a unit rate, “$4.00 per kilogram.”
What to notice if they don’t solve the problem fluently:
Unsure about what to do with the numbers, 20 and five, and may speculate that the answer is 25 (20 + 5) or 15 (20 – 5) or 100 (5 x 20). This may indicate that the student needs opportunities to find simple unit rates, initially with physical or diagrammatic objects.
Calculates 20 ÷ 5 = 4 using repeated subtraction or skip counting backwards, i.e., 20 – 5 – 5 – 5 – 5 = 0 but is unsure of the meaning of the quotient, four, in context. May express the quotient as a single measure, “$4.00”, rather than as a unit rate, “$4.00 per kilogram.” This indicates that the student needs further experience in expressing the answers to division as rates, where appropriate, so they come to understand the significance of ‘per’ as a connection between two measures.
Supporting activity:
Finding unit rates
- Onions cost $6.00 for 4 kilograms. How many kilograms of onions do you get for $24.00?
Ensure that both pencil and paper, and a calculator are available to the student and encourage them to use these tools.
Signs of fluency and understanding:
Creates a rate table to solve the problem, as below:
Notice that 24 is 6 multiplied by 4 so multiply 4 x 4 = 16. Interpret the result as 16 kilograms of onions.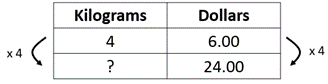
Note: This is a within strategy as the student works ‘within’ each measurement field.
May look for a unit rate by division, 6 ÷ 4 = 1.5, and interpret 1.5 as $1.50 per kilogram. Divide 24 ÷ 1.5 = 16 and interpret the result as 16 kilograms of onions.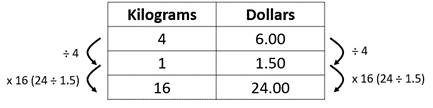
Note: This is a between strategy as the student works ‘between’ the measurement fields to create a unit rate.
May use an algorithm to find the missing value, i.e. 4 x 24 = □ x 6. 4 x 24 = 96, 96 ÷ 6 = 16. This strategy does not, by itself, signal understanding as it is unlikely the student can explain why the algorithm works.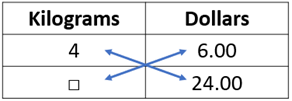
What to notice if they don’t solve the problem fluently:
Tries various operations with the numbers to find a result that seems reasonable. For example, the student may subtract 24 – 6 = 18 or 24 – 4 = 20, and state that the answer refers to the number of kilograms or onions. This indicates that the student has yet to see rate problems as involving multiplicative relationships.
Supporting activity:
Working with equivalent rates
- You pay $6.00 for 4 avocadoes. How much will you pay for 10 avocadoes at the same price?
Ensure that both pencil and paper, and a calculator are available to the student and encourage them to use these tools.
Signs of fluency and understanding:
Either mentally or using a recording strategy (possibly a rate table), creates an equivalent rate to 6 dollars for 4 avocadoes and multiplies that rate. Two likely examples are: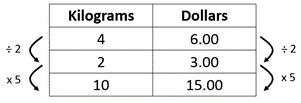
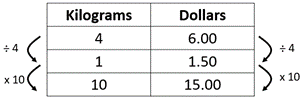
Note: Both are within strategies.
Either mentally or using a recording strategy (possibly a rate table), creates a relationship between measures. With the quantities involved this strategy is least likely.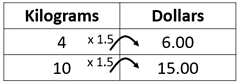
With all strategies the student communicates the meaning of the operations and refers to both numbers and units of measure in providing their answer.
What to notice if they don’t solve the problem fluently:
Uses an additive rather than multiplicative relationship between the number of avocadoes and dollars. One possible incorrect example is: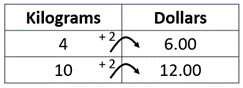
Uses an additive rather than multiplicative relationship within the number of avocadoes and within dollars. One possible incorrect example is: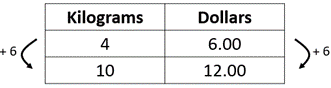
Both strategies indicate that the student needs experience with applying multiplicative strategies to rates.
Supporting activity:
Applying multiplication and division to rates
- You pay $28.00 for 10 litres of petrol. How much will you pay for 2.5 litres at the same price?
Ensure that both pencil and paper, and a calculator are available to the student and encourage them to use these tools.
Signs of fluency and understanding:
Either mentally or using a recording strategy (possibly a rate table), uses a within or between strategy involving a fractional, or decimal, multiplier.
Between strategy.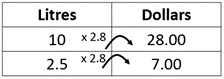
Within strategy.
The student might halve both measures and halve again to get 2.5 litres cost $7.00.
In all cases the student explains their strategy and refers to both measures in expressing the rate. For example, “2.5 litres are one quarter of 10 litres. Dividing $28 by four gives $7 so it costs $7 to buy 2.5 litres of petrol.”
What to notice if they don’t solve the problem fluently:
May speculate about a possible answer using the numbers involved. For example, 2.5 litres are less than half of 10 litres, so the answer is less than half of $28.00. In doing so, the student may show elements of understanding.
May apply incorrect additive thinking, such as recognise that 2.5 is 7.5 less than 10 and calculate 28.00 – 7.5 = $20.50. This indicates the student needs experience in applying multiplicative relationships.
Supporting activity:
Working with rates and fractions