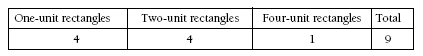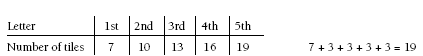These are level 2 number, algebra, and geometry problems from the Figure It Out series.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (370 KB)
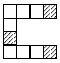
find rectangles within a shape (Problem 1)
solve problems using additive strategies (Problem 2)
continue a spatial pattern (Problem 3)
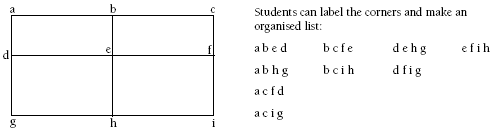
Problem One
This is a similar problem to Problem One on page 5. It can be solved using the same strategies.
Similarly, they might classify the rectangles as made up of one, two, or four smaller rectangles:
Extend the problem by adding another column or row to the figure.
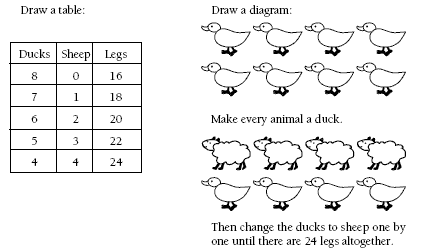
Problem Two
Knowing that, in general, ducks have two legs and sheep have four legs is important. Students may use a variety of strategies.
Change the conditions of the problem to see whether students have generalised the process. For example:
“There are nine animals and 30 legs. How many ducks are there?”
Problem Three
Making a table or writing an equation are useful strategies.
Students should recognise that three tiles are added each time to increase the letter size. This can be highlighted by building the letters on an overhead projector.
Students might solve other letter-building sequence problems, such as:
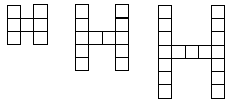
Problem Four
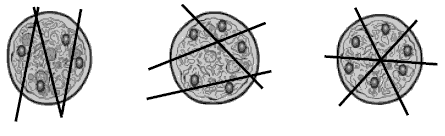
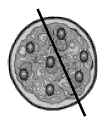
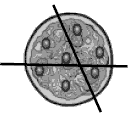
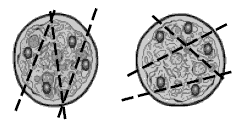
Students may solve the first two cutting problems randomly, but they will need to be systematic with the pizzas containing six and seven olives:
For example, with the seven-olive pizza:
Make the first cut so that four olives are on one side and three olives on the other.
Make the second cut so that the three olives are divided into one and two and the four olives are divided into two and two.
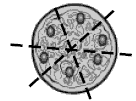
This leaves three sections the three olives are divided with two olives in each,
which need to be divided by the third cut:
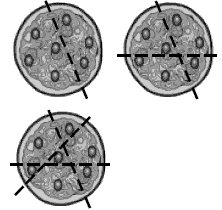
As an extension, ask the students to draw a pizza with eight olives and to make three cuts that leave each olive in a piece by itself. This is impossible and should lead students to realise that seven olives is the maximum number possible with three cuts.
Answers to Problems
1. 9 rectangles
2. 4 ducks
3. 19
4. Pizzas a and b: various answers, for example:
Pizza c:
Pizza d: three steps: