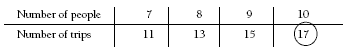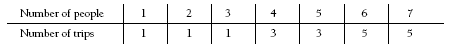This is a level 2 algebra strand activity from the Figure It Out series.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (309 KB)
continue a pattern and find a rule
counters or multilink cubes
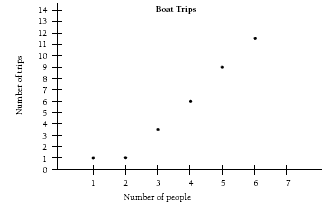
The boat-crossing problem is an excellent way of getting students to describe relationships. The students will need to carefully find the correct number of trips, using counters, physically moving themselves and other classmates across the room, or drawing diagrams (see diagram in the Answers section).
Organising the information into a table is a useful way to look for patterns.
The pattern for the first two people is misleading, but after that, the pattern settles down to two more trips being required for each extra person. On a relationship graph, this appears as a linear (straightline) pattern, which can be used to predict unknown values:
Students may use the “going up by two” rule to extend the pattern and find the number of trips required for 10 people.
Given the larger boat with a capacity of three people, the number of trips required becomes fewer and follows the pattern:
The repeating pattern of odd numbers is due to the net capacity of the boat being two people.
That is, although the boat carries three people, one person must row the boat back to the other side, so only two people have completed their trip across the river.
Answers to Activity
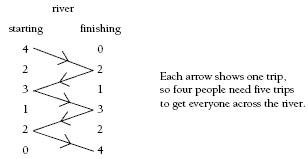
1. a. 3 trips
b. 5 trips
c. 7 trips
d. 9 trips
2. Two more trips are needed for each extra person after the first two people:
3. 17 trips
4. The pattern would be a repeating pattern of odd numbers, with two more trips for each extra two people after the first trip:
• 1 trip for 1, 2, or 3 people
• 3 trips for 4 or 5 people
• 5 trips for 6 or 7 people.