Problems on the Way to School

In this activity, students solve multiplicative problems drawn from everyday contexts.
Key mathematical concepts to focus on are:
• multiplication and division involve making equal groups and then working with those groups to count more quickly
• by applying addition and subtraction strategies, unknown multiplication facts can be derived from facts that students already know.
Working out what mathematics is needed to solve a word problem can be challenging for students. As a first step, encourage the students to discuss what maths they will need, and as a second step, ask them to write what the problem is asking as a number sentence, for example, 14 x 3 = or 120 ÷ 60 = .
The students will need to work out how many animals there are in question 1 from the fact that they have 18 eyes. An extension question could be to find out how many claws there could be. (Dogs have 5 claws on each paw [although often the small dew claw on each back foot is removed for safety reasons] and cats have 5 claws on each front paw and 4 claws on each back paw.) Ask: You don’t know exactly how many cats and dogs there are, only that there are 9 in total: what’s the least and most number of claws there could be?
For question 2, encourage students who are transitioning to stage 6 to look for multiplicative ways of grouping and counting 14 x 3 rather than just skip-counting in threes or adding 14 + 14 + 14. Using place value materials such as canisters and beans to represent 3 x 14, the students may be able to find alternative ways of grouping by moving the materials into different arrangements.

Possible multiplicative strategies include:
• working out 3 lots of 14 rather than 14 lots of 3. This involves understanding that changing the order of the factors gives the same result (the commutative property of multiplication).
• breaking the 14 into smaller groups and using known facts to work with those smaller groups:
(3 x 10) + (3 x 4) = 30 + 12 = 42. This strategy involves using the distributive property of multiplication over addition. The sets of 14 are distributed into sets of 10 and 4.
• halving one factor and doubling the other to create a known fact: 14 x 3 = 7 x 6 = 42
• multiplying by a tidy number and then compensating: working out 15 lots of 3 and then subtracting 1 lot of 3: (15 x 3) – (1 x 3) = 45 – 3 = 42.
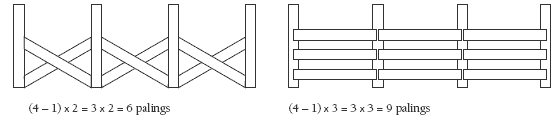
Talk about which parts of the fence in question 3 are posts and which are palings. Encourage students who are transitioning to stage 6 to look for multiplicative ways of solving the problem rather than just skip-counting in 4s. One way to promote this is to record the numbers of posts and palings as 1 + 4 + 1 + 4 + 1+ 4 + 1+ 4 + 1+ 4 + 1+ 4 + 1+ 4 + 1+ 4 + 1 = total number of posts and palings. Ask the students:
• If you know that there are 9 posts (the 1s), how many groups of 4 palings would there be? (8)
• If the fence was shorter and there were only 5 posts, how many groups of 4 palings would there be? (4)
• If the fence was longer and there were 16 posts, how many groups of 4 palings would there be then? (15)
• What pattern can you see that helps you work out how many groups of 4 palings there are if youknow how many posts there are? (There is always one fewer group of 4 palings than there are posts.)
Possible multiplicative strategies for working out 8 x 4 could be:
• breaking the 8 into smaller groups and using known facts to work with those smaller groups, for example: (4 x 4) + (4 x 4) = 16 + 16 = 32
• doubling repeatedly: 2 x 4 = 8, 4 x 4 = 16, 8 x 4 = 32
• using a known fact and compensating: (8 x 5) – (8 x 1) = 40 – 8 = 32.
Promote algebraic thinking by asking how many palings there would be if the fence had 6 posts (5 x 4 = 20 palings) or 21 posts (20 x 4 = 80 palings).
Extend the question by using iceblock sticks to create different fence structures. Ask the students: If you had  (a given number of) posts, how many palings would you need? How could you work this out without having to build the whole fence?

In question 4, some students may notice a link between 120 ÷ 60 = 2 and the basic fact 12 ÷ 6 = 2. Ask them to investigate whether this is true for similar examples, such as 150 ÷ 30 =  and 200 ÷ 50 = .
Extend part b of the problem by asking What about if you counted a spare tyre for each car as well? (7 x 5 = 35)
The students could use counters to help solve question 5. You could introduce the term “factor”: a number that is multiplied by another number to create a product. (See also the activity on pages 16–17.) If you divide a number by one of its factors, there will be no remainder. All the equalsized groups must be factors of 24, except that there are no children walking by themselves.
Encourage your students to use the multiplication facts they know to help them solve the problems in question 6. Challenge them to find alternatives to skip-counting by asking them to find another way to solve each problem and then to share and compare solution paths with the group.
Students who don’t know their 7 times table could solve 7 x 3 by reversing it to become a known fact, 3 x 7. However, you could also use 7 x 3 to demonstrate a multiplicative strategy that is useful for more difficult multiplications: that is, solving 7 x 3 by breaking the 7 down into smaller groups to create known facts and then adding the products together, for example:
7 x 3 = (3 x 3) + (3 x 3) + (1 x 3) = 9 + 9 + 3 = 21.
To solve 33 ÷ 3, prompt the students to use relevant facts they may know by asking: Do you know any multiplication facts that have 33 and 3 in them? How could you use that fact to solve this problem? Students who do not know that 33 ÷ 3 = 11 or 3 x 11 = 33 might use repeated subtraction to solve the problem, keeping track of how many groups of 3 they subtract, or they may need to use materials. Encourage these students to make the link between repeated subtraction and division by discussing the meaning of the ÷ symbol (“put into sets/groups of”) and asking them how they
could record what they did by putting numbers into the boxes in the following:  bins in groups of  makes  groups,  ÷  = (33 ÷ 3 = 11).
To solve the problems in question 7, students need to recognise the links between finding half of something and dividing by 2 and finding a third of something and dividing by 3. If your students have difficulty halving or thirding 3 066, ask them how they could break it up to make the calculations easier, perhaps by using place value partitioning to find half or a third of 3 000 and then of 66 or by breaking it up further to work with 3 000 + 60 + 6.
Question 8 asks students to make up their own problems. To avoid impossibly difficult problems being created, remind the students that they need to be able to solve (and explain the solutions to) all the problems on their map.
 

Answers to Problems

1. 9 tails and 36 paws. (Lachlan must have seen 9 animals if he saw 18 eyes: 18 eyes ÷ 2 eyes on each animal = 9 animals. Tails: 9 x 1 = 9. Paws: 9 x 4 = 36)
2. 42. (Using place value partitioning: 14 x 3 = [10 x 3] + [4 x 3] = 30 + 12 = 42
Using halving and doubling: 14 x 3 = 7 x 6 = 42
Using tidy numbers and compensating: [15 x 3] – [1 x 3] = 45 – 3 = 42.)
3. Methods may vary. (There are 32 palings.) Each post is followed by 4 palings, with an extra post at the end. Lachlan could count the posts, take 1 off the total, and multiply that number by 4. So, for this fence, 9 posts – 1 = 8 groups of 4
palings. 8 x 4 palings = 32 palings. Or Lachlan may have seen the posts and palings as groups of 5: (8 x 5) – (8 x 1) = 40 – 8 = 32
4. a. 2 hrs. (There are 60 min in 1 hr. 2 x 60 = 120 min or 120 ÷ 60 = 2)
b. 28. (7 x 4 = 28)
5. 2 groups of 12, 3 groups of 8, 4 groups of 6, 6 groups of 4, 8 groups of 3, 12 groups of 2.
6. a. 21 bins. (7 x 3 = 21)
b. 11 houses. (33 ÷ 3 = 11)
7. a. 1 533 steps. (Half of 3 000 is 1 500, and half of 66 is 33. 1 500 + 33 = 1 533)
b. i. 1 022. ( of 3 000 is 1 000, and of 66 is 22. So of 3 066 is 1 022.)
ii. 2 044. (1 022 x 2)
8. Maps and problems will vary.