These are level 3 geometry problems from the Figure It Out series.
A PDF of the student activity is included.
Click on the image to enlarge it. Click again to close. Download PDF (233 KB)
explore number of corners and faces in 3 dimensional shapes
Bit One
Students may not be aware of the convention of rounding up if the measure is exactly halfway between two measurement points. For example, a pencil that measures 14.5 centimetres would have that measure rounded up to 15 centimetres if a whole number was required. The discussion should embrace some interesting issues, such as “If it were the price of something, like $1.27, I would want it rounded down”; “If someone gave me half a cup of milk and told me it was rounded up to a whole
cup, I wouldn’t be happy”; “If I were trying for the high jump record, I’d like the height rounded up”.
Students need to realise that rounding up halfway linear measures is a convention, a widely accepted practice, and often there is no other explanation as to why it occurs. However, measuring someone for fitting clothes is a good reason why you should round up – it’s better to cut something too big than too small!
Bit Two
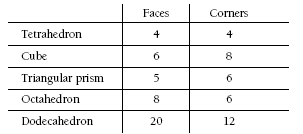
Students may need access to models of simple polyhedra, such as tetrahedra (4 faces), various prisms, octahedra (8 faces), and dodecahedra (12 faces). Encourage them to present their data in an organised format to support their belief.
For example:
The table reveals that three-dimensional solids do not always have more corners than faces.
Bit Three
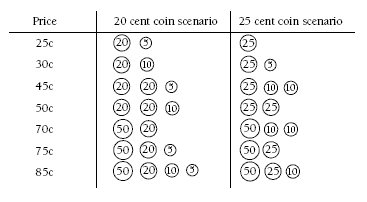
There is no one correct answer in this discussion. Students may focus on the way the two coinage systems could meet certain prices. For example:
The comparison indicates that for some prices, the 25 cent coin scenario would be advantageous because fewer coins are needed to make those amounts.
Answers to Problems
1. Answers will vary.
2. False; a tetrahedron has the same number of corners as faces.
3. Answers will vary.