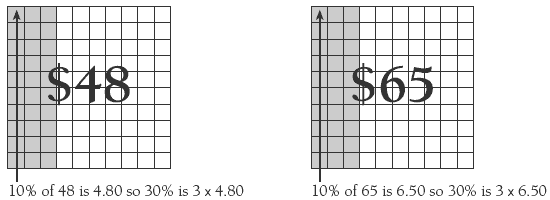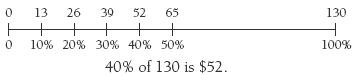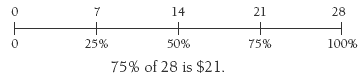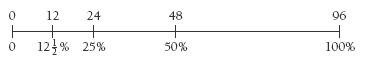Pondering Percentages

This activity gets students to represent fractions as percentages and to find percentages of money amounts using double number lines and 10 by 10 grids.
Decimals and percentages are special cases of equivalent fractions. For example, 75 percent is equivalent to 75/100, which is equivalent to 3/4 and many other fractions, such as 6/8, 15/20, and 30/40. Percentages can be used either as operators (scalars), to enlarge or reduce an amount by a given proportion, or as proportions in their own right. Just like fractions, they are used as both operators and numbers. For example, “20 percent of 35” treats 20 percent as an operator, and “6/24 is equivalent to 25/100 or 25 percent” treats 25 percent as a number.
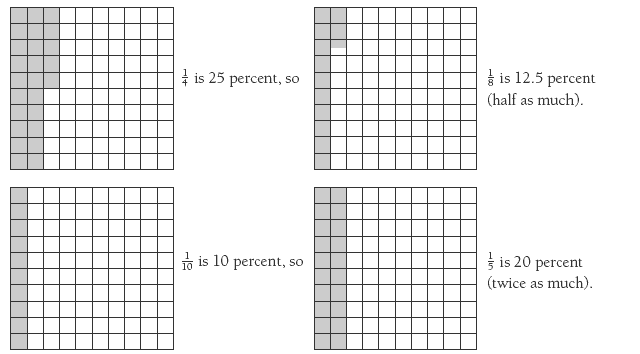
The first part of the activity treats percentages as numbers. It uses the hundredths grid to convert common fractions like 1/5, 1/4 , and 1/10 to percentages. The students can draw 10 by 10 grids in their exercise books and shade the appropriate fraction of the grid. Alternatively, you could give them cut-out squares to fold into the fractional parts.
Encourage the students to look for connections between the fractions and the corresponding percentages. Consider these connections:

From their experiences with percentages in contexts such as test marks and sports statistics, many students believe that percentages cannot be larger than 100, since 100 percent represents 1 or the whole. However, there are many real-life contexts, like lambing and calving rates and investment growth, in which percentages greater than 100 do occur. (If a farmer gets twice as many lambs as he has ewes, the lambing percentage is 200 percent.) Encourage the students to generalise this:
1 = 100 percent, so 2 = 200 percent, so 4 = 400 percent, and so on.
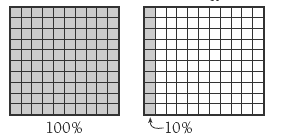
Question 2 involves using percentages as operators. The students’ book uses a hundredths grid to show this. If, for example, 30 percent of a grid is shaded, the grid can be used to find 30 percent of any amount:

Note that with the hundredths grid, the value of each small square, or hundredth, of the amount can be calculated if necessary and is equivalent to 1 percent. For example, 1 percent of $65 is 0.65 (65 cents) because 65 ÷ 100 = 0.65. So 32 percent of $65 could be calculated by 0.65 x 32 or by adding 0.65 + 0.65 to 30 percent of $65.
A double number line can also be used to find a percentage of any amount. For example, 30 percent of $48 can be shown as:

Double number lines allow the students to solve difficult percentage problems by connecting and co-ordinating more manageable calculations. The double number line reflects the multiplicative relationship between the fraction and the percentage. For example, consider the problem “35 percent of $56”. The order of calculation might be: 10 percent of 56 is 5.60, so 30 percent of 56 is 3 x 5.60 = 16.80, and 5 percent of 56 is 1/2 of 5.60 = 2.80. 35 percent is 30 percent + 5 percent = $19.60.

For more ideas on how to develop double number lines to solve percentage problems, refer to pages 31–34 of Book 7: Teaching Fractions, Decimals, and Percentages in the Numeracy Project series.

Extension

To challenge the students further, pose problems where the conversions to percentages are not tidy and the students need to approximate the answer. You can do this by making the percentage and the money amount untidy, for example, “find 67 percent of $47.95”. In real-life situations, it is often enough to estimate the answers to such problems. 67 percent is about two-thirds, $47.95 is about
$48.00. 2/3 of 48 is 32. So $32 is a close estimate.
Encourage the students to use rounding and their knowledge of percentage to fraction conversions to help them estimate the answers to percentage problems.
 

Answers to Activity

1. Yvette. 1/5 is 2/10. 1/10 = 10%, so 1/5= 20%.

Leonie
1/2 = 50%, and 1/4 is half of 1/2 , so 1/2 of 50% must be 25%.

Andrew
Yes, you can. 110% would be 1 more than 1.

2. a. Answers and a possible method for each (based on one of the ideas shown) are:
i. $11. 10% or 1/10 of 55 is 5.50. So 20% is 2 x 5.50 = $11.00
ii. $12. 10% of 80 is 8. 5% is 4. 8 + 4 = $12
iii. $52

iv. $21

v. $38. 95% is 100% – 5%. 10% of 40 is 4, so 5% is 2. 40 – 2 = $38.
vi. $60. 100% of 48 is 48. 25% of 48 is 12. 48 + 12 = $60.
b. Discussion and opinions will vary. (All the methods will work.)
c. Answers and a possible method for each (based on one of the ideas shown) are:
i. $14.40. 50% of 36 is 18;
10% of 36 is 3.60; 18 – 3.60 = $14.40
ii. $28. 10% of 35 is 3.50;
3.50 x 8 = $28
or 35 – 3.50 – 3.50 = $28
iii. $15.60. 50% of 24 is 12;
10% of 24 is 2.40; 5% of 24 is 1.20;
12.00 + 2.40 + 1.20 = $15.60
iv. $12