Planning Paths

This activity encourages students to think systematically about the structure of a pattern and to predict patterns through the use of generalisations or equations. Students need to be at least early additive part–whole thinkers (stage 5) to do this activity mentally, although students working at earlier stages may be able to do so with the support of materials like pattern blocks.
You could set the scene with a guided teaching group by talking about “makeover” shows on TV: What would you have done to your house and garden if you were on one of these shows?
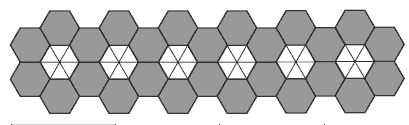
Get the students to use foam pattern blocks to make a path using triangles and hexagons, as pictured.

Ask: If we wanted to add another flower to the path, how many more triangles and hexagons would we need?
In question 1, the diagram and the table (which uses numbers to represent the tiles) are designed to help the students see how the pattern is formed. For each new flower, 4 hexagons and 6 triangles are needed, but for any path, there are always 2 extra hexagons needed to complete the last flower (or to start the first). Some students may need to make paths with 1 flower, 2 flowers, 3 flowers, and so on to help them visualise these relationships.
Students should find it straightforward to add on 1 more flower at a time, but it is important that they look beyond iterative (sequential) rules such as “add 4 hexagons and 6 triangles” because these rules are only helpful if you know how many of each type of tile were used in a path with 1 fewer flower. A general pattern or generalisation enables students to work out how many tiles are needed for any length of path and is therefore much more powerful. To encourage the students to look towards the generalisation, ask questions such as:
What short cuts could Kalila use to make it faster than adding on 4 hexagons and 6 triangles every time?
Multiplication is a fast way of adding. What could you work out instead of 4 + 4 + 4 + 4 + 4?
Can you see any groups that Kalila could multiply to make a path with 12 flowers? (12 groups of 4 hexagons [12 x 4] and 12 groups of 6 triangles [12 x 6], then add the extra 2 hexagons)
If you make a 12-flower path and you multiply 12 x 4 hexagons and 12 x 6 triangles, would this give you all the tiles you need? How do you know?
If the students think that 48 hexagons and 72 triangles would be enough, encourage them to test this with a smaller number, such as the 4-flower pattern drawn or one they’ve made, or to use the patterns in the table to see that they’d need to add another 2 hexagons on. Could you use the same short cut for 20 flowers? How could you test to check?
In question 2, watch for students who assume that the 16-flower path will just have double the tiles needed in the 8-flower path. Challenge their thinking by saying:
Convince me that you’re right.
How could you test that?
Does that strategy work for patterns that you’ve made?
Could you test your strategy on the 2-flower and 4-flower path in the table?
Question 1c requires students to apply their patterns and short cuts to writing a generalisation for any length of path. To promote algebraic thinking, say to the students:
Describe what you would do to work out how many tiles you’d need for a really long path.
Write a list of instructions for someone else to follow your short cuts. (To work out the number of hexagons, multiply the number of flowers in the path by 4 and then add 2 more to finish the last flower. To work out the number of triangles for the centres of the flowers, multiply the number of flowers in the path by 6.)

Investigation

Encourage the students to lay their pattern out in a way that makes a short cut clear, like the diagram of the flower path in the student book.

Extension

Have the students work backwards: Kalila used 86 hexagonal tiles. How many flowers did she make?
How many triangular tiles did she need?
The students could also consider the equivalence of different rules for the same pattern. For example, Mike says that for 12 flowers, it will take (12 x 6) – (11 x 2) hexagons. Where do his numbers come from?

Answers to Activity

1a.

b.

c. Number of hexagonal tiles = (the number of flowers x 4) + 2
Number of triangular tiles = the number of flowers x 6
2. a. (8 x 4) + 2 = 34 hexagonal tiles and 8 x 6 = 48 triangular tiles
b. (16 x 4) + 2 = 66 hexagonal tiles and 16 x 6 = 96 triangular tiles
c. (100 x 4) + 2 = 402 hexagonal tiles and 100 x 6 = 600 triangular tiles

Investigation

1.–2. Practical activity