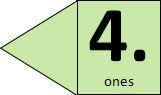
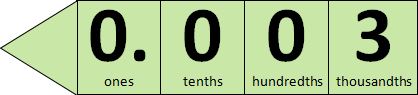
The purpose of this unit is to build on students’ understanding of place value with whole numbers and decimal fractions. It supports students as they make generalisations using their conceptual place value understanding across our numeration system.
- Recognise the importance of zero as a place holder in whole and decimal numbers.
- Recognise the repeating pattern of hundreds, tens, and ones in numbers up to, and beyond, one million.
- Correctly read and name whole numbers and decimals up to, and beyond, one million.
- Appreciate and understand the size of one million and beyond.
- Demonstrate understanding of the powers of ten.
- Understand what a decimal fraction is and recognise that they arise out of division.
- Understand that the decimal point is a convention that separates whole units from parts of a unit.
- Recognise that our base-ten place value system extends indefinitely in two directions.
Understanding place value is crucial if students are to develop the estimation and calculation skills necessary to become numerate adults. Our number system is based on groupings of ten. Ten ones form one ten, ten tens form one hundred, ten hundreds form one thousand, and so on. The continuation of this system allows us to represent very large quantities. Therefore, the mathematical ideas developed in this unit will enable students to apply their understanding of the base ten system, to identify, group, name, and make calculations with an increasingly large and complex library of digits and numerals.
The place values in this system, such as one, ten, one hundred, one thousand, and so on, are powers of ten. Therefore, the place immediately to the left of a given place represents units that are ten times more than the given place, e.g. thousands are ten times greater than hundreds. The system also continues to the right of the decimal point, giving us the capacity to represent very small quantities (e.g. tenths, hundredths, thousandths, and so on).
Understanding, and being able to apply knowledge of decimal place value involves more than knowing the significance of the position of digits in a whole number, (e.g. the knowledge that the 7 in 24.671 means seven hundredths). Strategies for computation require a nested view of place value and understanding of the scaling effect that occurs as digits move to the right and left in place value. This means that nested in the ones are tenths, hundredths and thousandths in the same way that nested in the hundreds are tens, ones, tenths, and so one. Therefore, 3.509 has 35.09 tenths, 350.9 hundredths, 3509 thousandths, and so on. This is integral to understanding the multiplicative nature of our numeration system.
Links to the Number Framework
This unit is linked to stages 6 and 7 of the Number Framework.
This unit complements lessons found in Book 5, Teaching Addition, Subtraction and Place Value.
The learning activities in this unit can be differentiated by varying the scaffolding provided or altering the difficulty of the tasks to make the learning opportunities accessible to a range of learners. Ways to support students include:
- reducing the number of digits, and therefore the size and complexity of numerals, that students are asked to work with
- providing open access to a variety of materials for modelling numbers (arrow cards, Multibase Arithmetic Blocks, place value houses)
- providing opportunities for explicit and direct teaching, small group teaching, and for paired and group work
- using the digital learning object Modeling Numbers: 6-digit numbers to provide support with reading and writing numbers.
This unit is focussed on the place value structure of whole numbers and as such is not set in a real world context. Learning to read and write numbers in Māori or other Pacific languages will support students’ developing understandings, because number names are derived from their place value structure in these languages. When developing understanding of the different sizes of the numerals featured in this unit, consider also how links could be made to the cultural makeup, learning interests, other curriculum areas, and real-world contexts that are relevant to your students.
Te reo Māori kupu such as miriona (million), ira ngahuru (decimal point), hautanga ā-ira (decimal fraction), whakarea (multiply, multiplication), and whakawehe (divide, division) could be introduced in this unit and used throughout other mathematical learning.
- Place value houses (Trendsetter, Thousands and Millions) (MM 4-11)
- Zap game
- Copymasters One, Two and Three
- Copy of the book How much is a million? by David M. Schwartz (available online)
- Arrow cards (MM 4-14)
- Decimal arrow cards (MM 7-2)
- Interlocking or Unifix cubes
- MAB (Multibase Arithmetic Blocks), 1, 10, 100, 1000, also known as Dienes blocks
- Play dough
- Plastic knives
- Chart paper/resources
- The digital learning object Modeling Numbers: decimals
This unit includes five sessions, each with a number of learning activities. These sessions could be taught in succession over a number of days to provide a concentrated focus on building place value knowledge. Alternatively, selected sessions or activities could be used to support place value understanding, as part of small group teaching sessions, while other students work on solving number problems. You could use the activities as an introduction to a particular number concept, and then use the remaining time to revisit and consolidate knowledge of these concepts, with specific students, in response to their demonstrated knowledge.
Session 1
SLOs:
- Appreciate and understand the size of one million.
- Understand and describe the multiplicative nature of our base ten number system.
Activity 1
- Begin the lesson by writing a 4, 5 or 6 digit number on the place value houses, using an erasable whiteboard marker. Include numbers that have one or more zero as a placeholder. Have students read the number to themselves then read it aloud to a partner. Address any gaps in knowledge that arise around correctly reading out the names of these numbers.
- Together, select a digit to remove and erase this from the chart. Ask students to tell a partner how much was removed (e.g. five hundred, three thousand).
What was the value of the digit that was removed?
Leave the empty space and see whether the students tell you that a zero must be written there. If not, do this and ask the students why the zero is needed. - Introduce the game Zap (Book 4 Teaching Number Knowledge, p26) to the class.
- Distribute calculators and have students play Zap in pairs. Have them record the numbers made and the amounts removed as they take their turns.
Activity 2
- Show the dot image of 10 000 from Copymaster 1.
Ask:
How many dots are here and how do you know?
Repeat with the image of 100 000 dots. Pose the question:
What would 1 million dots look like?
Have students discuss this in pairs and allow time for them to write down their ideas. - Read How much is a million? by David M. Schwartz and discuss. You may wish to do this activity linked to the book.
- Have students share their ideas of how much one million is. Display 10 pages of 100 000 dots, asking "Is this one million? How do you know?”
- Draw one dot on the class chart and write beside it 1 x 10 = 10. Draw ten dots beside the expression.
- Begin listing this pattern, having the students complete each equation. 1 x 10 = 10 10 x 10 = (100) 100 x 10 = (1000) 1000 x 10 = (10 000) 10 000 x 10 = (100 000) 100 000 x 10 = (1 000 000)
- Ask students what they notice about the notation 1 000 000 and record their ideas about “How much is a million?”. Ensure students notice that one million is one thousand lots of one thousand. You could make a ‘One Million Book’ in which children record their ideas in an ongoing way and in which are pasted copies of the 10 pages of 100 000 dots. This could also be done by small groups or pairs, with the final ‘One Million Book’ being collated by the teacher.
- Introduce exponent notation, 102, 103, 104, 105, 106, explaining that this is another way (a shorthand way) of showing how many times ten is multiplied by itself. For example, write and show 10 x 10 x 10 = 1000, ten multiplied together three times is one thousand.
Activity 3
- Have students plan a “One Million Investigation”. For example:
- How long would my favourite book be if it had one million words?
- How old would you be if you lived one million seconds?
- How long would you have lived if you’d had one million breakfasts?
- How long would it take you to take one million breaths?
- How long would the line be if you lined up 1 million one centimetre cubes side by side? Which two real-world locations are this distance apart?
Ensure you set clear parameters for this investigation - such as method of presentation (e.g. act it out, created with a relevant digital tool, written, verbal, video, poster, PowerPoint). These investigations could also include the most interesting facts students have learnt about one million. Consider organising students into groups with mixed levels of mathematical knowledge and confidence in order to encourage greater peer learning and scaffolding, and collaboration.
- Have students present their findings to the class. Include these findings in the class ‘One Million book’ (developed in the previous session). Have students discuss how they could share what they have learned with their parents and whānau.
Session 2
SLOs:
- Recognise the repeating pattern of hundreds, tens, and ones in numbers up to, and beyond, one million.
- Demonstrate understanding of the powers of ten.
Activity 1
- Ask a student to write one million in numerals on the class chart, or ask students to do this independently (e.g. on a mini whiteboard, on working paper). Note the spaces between 3 digits (1 000 000) and ask for an explanation of this. Look for students to recognise that the hundreds, tens and ones naming structure is being repeated.
- Have students predict what the Millions place value house will look like, then display this.
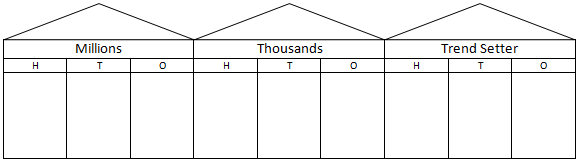
Write a range of 7, 8 and 9 digit numbers. Emphasise the hundreds, tens and ones naming in each house, and highlight how to correctly read numbers including zeros (e.g 703 206). - Write a 7-digit number and have students give some examples of things that are counted in millions in the real-world. For example, money ($3,000,000 might buy an expensive house), populations (there are over 5 million people in NZ), distances in space (it is 152 million km from earth the sun), years dating to the past (dinosaurs became extinct about 65 million years ago), and stars (there are 10 million stars in the giant star cluster Omega Centauri).
- Highlight for your students that we use commas to separate the groups of three digits when we are writing amounts of money. However, spaces are used in other contexts (except when writing 1000).
Activity 2
Show the students Copymaster 2 and have them work in pairs to write down five interesting things they notice about this chart. Have them write some of the numbers themselves, making the connection as they do so between the exponent and the number of zeros. Share the discussion points with them.
Activity 3
Have the students play the game Powers or Bust (Copymaster 3).
Activity 4
Challenge students to write, in less than 200 words, a response to the question, “Our base ten numeration system is useful because….” Encourage students to consider relevant contexts in which they use the base ten system. Have the students share their responses. This should generate some valuable discussion. Use this opportunity to identify and address any place value misconceptions.
Session 3
SLOs:
- Understand what a decimal fraction is and recognise that they arise out of division.
- Correctly read and name whole numbers and decimals up to, and beyond, one million.
Activity 1
- Begin the lesson reviewing the place value structure of whole numbers, using place value houses. Emphasise the repeated hundreds, tens and ones naming structure.
- Have students discuss what happens when you divide a big number by ten. (You may like to refer to their experiences playing Powers or Bust.)
Write 1 000 000 on the PV house and discuss dividing this number by 10. It may be helpful to use the ten images of 100 000 dots (1 million) and demonstrate that one tenth of the ten images is one of them (100 000). Model repeated division by ten until one is reached. This can be powerfully demonstrated using the dot images from Copymaster 1. - Ask the students to discuss in pairs which number is the start of our whole number system (responses may include zero, one, ten). Establish that one is the number with which we begin. We either increase 1 by powers of ten (e.g. 10, 100, 1000, and so on) or decrease 1 by powers of ten (e.g. 10ths, 100ths, 1000ths, and so on).

- Write 1 in the ones place on the place value houses. Have students discuss what happens when we move to the right of one, in other words if we divide, and keep on dividing. Make links to students’ knowledge of multiplying (e.g activity two in session one looked the following expressions: 1 x 10 = 10 10 x 10 = (100) 100 x 10 = (1000) 1000 x 10 = (10 000) 10 000 x 10 = (100 000) 100 000 x 10 = (1 000 000).
- Record the students’ ideas. Listen for important misconceptions. For example “there is a decimal point next then it goes ones, tens, hundreds the other way” (an understanding of symmetry around the decimal point) or this may be expressed as “oneths, tenths, hundredths”. Alternatively no symmetry may be assumed. Some may suggest that the naming pattern continues unchanged hundreds, tens, ones.
Activity 2
- Distribute a small ball of playdough, a plastic knife, chart paper and a pen to student pairs. Explain that the playdough represents "one" (like the one dot shown on Copymaster 1).
- Challenge the students to work with the materials to show and record what happens when one is divided. This should reflect the place value pattern of numbers.
Do not mention tenths, hundredths etc. at this point. Also explain that they may have to reshape their play dough ‘one’ to work with it more easily. - Observe the students' actions. Have them pair share their charts and explanations. Summarise what the students’ work has revealed and discuss this.
- Model the activity for the class to see. Take the one ball and divide it into ten balls, then take one of those and repeat. Emphasise how quickly the size of the balls changes and highlight the magnitude of division by ten each time.
- Comment that students may have made a ‘sausage’ with their ball and worked that way. The representation is the same.
- Use a brightly coloured, round sticker and place this over the decimal point to emphasise its importance. Have students discuss in pairs and write an explanation to complete this statement:
This very important dot is... - Have students share what they have written. If key ideas are not been highlighted by the students, emphasise:
- the decimal point is a convention that separates a whole unit (one) from parts of a unit (tenths)
- the importance of one as the start of our number system (the tenths place is tenths of ONE, and the tens place tens of ONES)
- that the numbers that follow the decimal point are called decimal fractions, which are a special kind of fraction with a tens base
- decimal fractions are the result of division.
Activity 3
- Using the class/group chart, write decimal numbers to one or two places (in words). Have students come forward and write the numeral representation.
- Reverse the process in step 1 above. Write a decimal number and have students correctly read the decimal number and write it in words. Listen for, and highlight correct reading, for example 0.43 is read as "zero point four three" NOT "zero point forty three". Address any misconceptions about reading a decimal number that arise.
Activity 4
Conclude the lesson by having the students individually write a reflection on what they have learned.
Encourage students to illustrate their reflections with pictures/diagrams.
Display some of the students’ work from this session.
Session 4
SLOs:
- Recognise the importance of zero as a place holder in whole and decimal numbers.
- Recognise that our base ten place value system extends indefinitely in two directions.
Activity 1
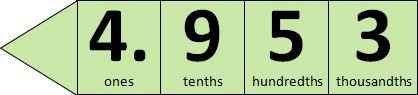
- Draw a decimal place value house on the class chart and write several decimal numbers. Distribute decimal arrow cards to the students.
- Have students take turns making the numbers using the arrow cards and reading them to each other in at least two ways.
For example:
|
4.953 is read as "four point nine five three"; "four and nine tenths, five hundredths and three thousandths"; "four and nine hundred and fifty three thousandths"; or as "four and ninety five hundredths and three thousandths".
3.05 is read as "three point zero five" or as "three and five hundredths".
7.029 is read as "seven point zero two nine"; "seven and two hundredths and nine thousandths"; or as "seven and twenty nine thousandths".
- Discuss that thousandths are 1 ÷ 10 ÷ 10 ÷ 10 and that that pattern of dividing by 10 can continue.
Activity 2
- Have students work in pairs to brainstorm contexts they can think of in which ONE might be divided into tiny parts. Examples might include time (Usain Bolt can run 100m in 9.58 seconds, measurement of tiny things that can only be seen under a powerful microscope (a bacterial cell is 5 millionths of a metre long), weight (a small apple might weigh one tenth of a kilogram) and volume (one teaspoon is 5 thousandths of a litre).
- As a class share ideas and record these on a class chart. Demonstrate how the decimal place value chart continues to the right (go to six places: tenths, hundredths, thousandths, ten thousandths, hundred thousandths, millionths). Ask, “Does it keep going?’ and discuss.
- Challenge students to investigate ‘infinity’ and present their own statement or diagram to describe ‘how it works’.
Activity 3
- Present students with this statement:
Zero is worth nothing and it is therefore of no use in decimal numbers.
In pairs or small groups have students consider and investigate this, be prepared to agree or disagree with the statement, and give evidence to support their position (justify). - When the students are ready, have them move to one side of the room or the other, showing their agreement or disagreement.
Have them present their rationale using illustrations to make their point.
NB. Zero is an important placeholder, just as in whole numbers. However, unlike with whole numbers, if a zero is added to a decimal number it does not change its value. For example 4.5 = 4.50
Session 5
- Read and write decimal numbers to three places.
- Recognise the importance of zero as a place holder in whole and decimal numbers.
- Recognise that the grouping pattern extends to the right of the decimal point.
- Recognise that our base ten place value system extends indefinitely in two directions.
Activity 1
- Show students the digital learning object Modeling Numbers: decimals. Explain that it provides a model for representing numbers using place value equipment. Clicking on the arrow above a place adds one unit in that place to the model of the number, and clicking on the arrow below a place removes one unit from that place in the model.
Note that clicking the right arrow at the bottom of the screen will show different representations of the number: using place value houses, in standard form or represented on a three bar abacus.
- Show students how the learning object works by making the numbers 6, 7, 8, 9 and 10 (by clicking on the arrow above the ones place). Ask the students what they think will happen when you make the number 11, then make the number and watch what happens. Ask the students what they think will happen if you count backwards 11, 10, 9. Then watch the place value equipment change as you remove one at a time using the arrow below the ones place.
- Repeat this, starting with the number 1 and asking what will happen when you remove one-tenth (by clicking the arrow below the tenths place). Zoom in using the magnifying icon and watch what happens.
- Repeat twice more, removing one hundredth from one tenth, and one thousandth from one hundredth.
Activity 2
Have students work in pairs to model numbers on the learning object. They can click the die at the bottom left of the screen and a number will appear in words for the students to build using the place value equipment. They can click on the question mark symbol to check to see whether their model is correct.
Activity 3
Have students work in pairs to explore making their own number, saying it aloud and then checking whether they are reading the number correctly using the speaker icon.
Dear parents and whānau,
In class we have been learning to understand large numbers, their value, and how to read them correctly. We have then used this knowledge to help us understand decimal numbers.
Ask your child to show you their poster about one million or to tell you what they have learned in their one million investigation.
Have them tell you and show you how our number system works. You may be surprised by what they tell you!