This unit supports students learning to understand the structure of two-digit numbers and how to operate with them.
Session One
- Group a set of objects in tens to aid in counting the objects.
Session Two
- Recognise how many tens and ones are in a given collection.
- Read two-digit numbers used to represent quantities.
Session Three
- Partition (break up) 100 into two numbers using tens and ones place value.
Session Four
- Rename two-digit numbers in many ways.
Session Five
- Change a two-digit number to a target number with one operation.
Our number system is sophisticated though it may not look like it. While numbers are all around us in the environment, the meaning of digits in those numbers and the quantities they represent are challenging to understand. Our number system is based on groupings of ten. This means ten is our preferred grouping for collecting single objects into groups. Using ten is so common around the world because humans have ten fingers. The part of our brain that controls our fingers is also associated with counting.
To represent all the numbers we could ever want we use ten digits, 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. The word for digits comes from the Latin word for fingers or toes - digitus - and related to the age-old practice of counting on fingers and toes. We don’t need a new number to represent ten because we think of it as one group of ten. When we use the numerals 10 to represent "ten" we are using place value for the first time. The place of the digit 1 tells us the size of the quantity it represents -one ten. Zero has two uses in the number system, as the number for ‘none of something’ and as a placeholder. That means it occupies a place, or places, in order to identify the values represented by the other digits. In the number 10, zero acts as a placeholder in the ones place.
Place value means that both the position of a digit as well as the value of that digit indicate what quantity it represents. In the number 73 the position of the 7 is in the tens column which means that it represents 7 units of ten (70). Renaming a number flexibly is important. In particular, it is vital that students understand that when ten ones are created they form a unit of ten. For example, the answer to 25 + 35 is 6 tens (60) because 5 ones and 5 ones combine to form another ten. Similarly, when a unit of ten is ‘decomposed’ into ones the number looks different, but still represents the same quantity. For example, 42 can be viewed as 4 tens and 2 ones, or 3 tens and 12 ones, or 2 tens and 22 ones. Decomposing is used in subtraction problems such as 72 – 48 = □ where it is helpful to view 72 as 6 tens and 12 ones.
This unit can be differentiated by varying the scaffolding of the tasks or altering the difficulty of the tasks to make the learning opportunities accessible to a range of learners. For example:
- providing place value materials, play money or a calculator for students to use if they need to check their answers. Work first with materials where ones can be combined to make tens (such as bundles of sticks or unifix cubes) and progress to materials which represent tens and ones differently (such as place value blocks or money)
- providing additional opportunities for students to practise modelling two-digit numbers on place value materials
- grouping students to share and justify their thinking.
Some of the activities in this unit can be adapted to use contexts and materials that are familiar and engaging for students. For example:
- using te reo Māori names when counting numbers, to reinforce the tens-based structure of numbers
- using environmental materials to model the tens and ones structure of two-digit numbers, for bundles of flax or korai sticks (flower stem of flax)
- incorporating relevant contexts, concepts, and objects that reflect the cultural diversity and current learning interests of your students (e.g. they could count groups of 10. takahē if they have been learning about native birds)
- working outside of the classroom on some activities.
Te reo Maori vocabulary terms such as uara tu (place value), poro-tekau (tens place value block), poro-tahi (ones place value block) and rautaki tatau (counting strategy) could be introduced in this unit and used throughout other mathematical learning.
Before you start this unit you may like to watch the video ‘Counting Collections’ in nzmaths.co.nz which focuses on developing number sense. As an introduction you could try ‘Count it’ for Yrs 1-3.
- Groupable materials such as: Ice block sticks and rubber bands, Lima beans and small plastic bags, Unifix cubes, BeaNZ and film canisters, counters and bags (only one type of material is needed)
- Calculators
- Slavonic Abacus
- Copymasters One to Five (see end of unit for links).
- Games of Cover Cathy Crocodile Tens and Ones (5 students per game)
- Access to internet
- Copymaster 1
- Copymaster 2
- Copymaster 3
- Copymaster 4
- Copymaster 5
Prior Experience
This unit is targeted at Level 2 so students should have experience of the following skills from Level 1:
- Forward and backward number sequences to 100 at least
- Counting and forming sets of objects to 100 at least
- Reading and writing numbers to 100 at least
If your students have not yet developed proficiency in these skills, consider revising them prior to, or alongside, this unit.
Session One
In this session the students explore how groupings of ten can be used to aid counting and to perform calculations. They create the sets of countable objects that will be used in later lessons. Consider framing the creation of these countable objects in relation to other relevant learning (e.g. creating painted stones for the school garden, collecting cans for a school-wide food drive).
Acknowledgment: The game 60 second challenge was created by Ann Downton from Monash University, Melbourne.
- Play the game “Sixty Second Challenge”. You need a measure for one minute (e.g. stopwatch, egg timer) and a lot of countable items such as beans, cubes, ice block sticks, or counters. You will use these countable objects as your place value material for the week at least. Set the timer for one minute. During that time the students work in pairs in this way. One partner rolls the dice and the other partner takes that many objects and adds them to their collection. Then the partner rolls the dice again and their partner collects that many objects. Rolling the dice cannot occur until the previous collection is made. When sixty seconds is up the students count how many objects they have collected in total. Each total can be recorded on a post-it note or a scrap of paper. Each pair needs to bring their number to the mat. Put a skipping rope on the ground (1m +) and label the ends 0 and 100 by pegging a card to each end. This activity can also be done outside with a chalk number line.
- Ask the students, one pair at a time, to place their score on the line where they think it belongs and peg the label to the rope. Discuss the placement in terms of proximity to benchmarks like 50, 75, 25, etc. After five numbers are placed, ask the remaining groups to put their score where they think it belongs.
- Discuss how students counted their collections. Look for different ways of grouping. Discuss which way is easiest. Counting in twos and fives is relatively easy but there are a lot of counts. Counting in threes is difficult because there is no pattern to the sequence to help you. Grouping in tens and ones makes writing the number easy to say and write. For example four groups of ten and six is ‘forty-six’ and is written as 46. You could revise these counting strategies with a video or song. Value all methods of counting, and consider pairing up students with similar times-table knowledge. This will help them to feel confident in their ability to share their knowledge with a peer.
- Play the “Sixty Second Challenge” with the players swapping roles of dice thrower and object gatherer. Look for students to group systematically to find the totals. Add the second attempt numbers to the number line. If there are many notes for a number the notes can be allocated to the same position on the line beneath one another. An interesting question is, “Is the class getting better at this game?” Ask students to justify their answers.
- Pose two questions related to the final game for students to solve. Discuss key words like total and difference.
What is the middle score? How can you tell?
What is the difference between the highest and the lowest score? - For the latter question, make the highest and lowest collections using groupings of tens and ones. “I am using tens and ones because I think that will be easier.” Organise the two collections on the place value mat (Copymaster 1) to create a useful image of difference. Below packets of beans are used and the lowest and highest totals are 24 and 87 respectively.
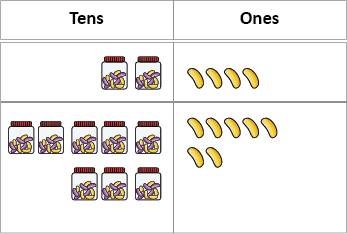
- Send the students off to solve the difference problem in pairs. Tell them to organise their counting objects in packets/groupings of ten. These groupings will be useful for the remainder of the week. So iceblock sticks might be bundled with rubber bands, cubes might be connected into lengths, and beans might be bagged in small see-through bags or white film canisters. Look for:
- Do your students use the groupings of ten to simplify the task rather than count in ones?
- Do they recognise that basic facts can be applied to groups of ten as well as ones, e.g. 8 tens is 6 more tens than 2 tens (20 + 60 = 80)?
- Do they combine tens and ones and name the quantity, i.e. 6 tens and 3 ones makes 63?
- Discuss these important ideas when you gather the class together to sum up what they have learned.
Session Two
In this session students learn to match quantities with two-digit numbers and vice versa.
Part One
- Have your students sit on the mat in a circle so they can all see an A3 sized place value mat you have put in the centre. Give each student a copy of a hundreds board (Copymaster 2) and one counter.
- Tell them you are going to say a number and they are to put their counter on it. Stress the importance of distinguishing “teens” from “tys”, for example sixteen from sixty. Some students may need more practice counting these types of numbers - they could be supported with the use of a song or by using flashcards with a partner.
- Once students are confident at listening and placing the counter on the correct number, introduce the counting objects (cubes, beans, iceblock sticks, something relevant to your classroom context etc.) packaged in tens from the previous day. Discuss how the objects are organised in sets of ten. Note that the A3 sheet is divided into two columns for tens (left) and ones (right).
- Play a game where you create a collection of objects (whole tens and ones) and the students indicate how many objects are in the collection by placing the counter on that number on the hundreds board. Focus on the language connection of “ty” as tens and “teen” as one ten. Some important ideas to think about when developing your sequences:
- teen and ‘ty’ numbers, e.g. 13, 17 compared to 30 and 70
- iterating by tens, e.g. 13, 23, 33, 43, … (Note that the ones digit does not change)
- re-unitising ten ones to form a ten unit, e.g. 67, 68, 69, 70.
- re-unitising ten tens to form a hundred unit, e.g. 97, 98, 99, 100. (Note that students must visualise the continuation of the hundreds board pattern to show numbers greater than 100.
- go backwards in sequences as well, e.g. 87, 77, 67, ...
- Move to masking where you create a hidden collection under a shield of some kind (card or plastic container) and tell the students information like:
There are four tens and seven ones.
It is not quite eight tens. There are three beans missing. - Repeat the process of iterating by tens. Start with a collection, say 24, then add ten repeatedly to the collection. Get the students to show the total each time by moving their counter. Go through 100 forwards and down to zero backwards. See if the students can “shortcut” several iterations of ten by using fact knowledge, e.g. 40 + 30 is just 4 + 3 in units of ten. Move to more complicated examples like:
I have 26 (put the collection under the shield). I am putting 60 more beans in. What does sixty look like (6 bags of ten). How many beans are there now? How do you know? - Compare the starting number and the final number using an empty number line:

Is there an easy way to know it will be 86 without going 26, 36, 46, ... 86? - Get the students to work in pairs with one student creating and building with physical collections and the other moving their counter to show the quantity on a hundreds board. Letting the counter mover see the collection or masking the collection is an important variable. More capable students could work with the hundreds board that is missing many numbers (See Copymaster 3) or use a different century from the Thousands Book (see Copymaster 4) using place value blocks to build the collections.
Part Two
- Play Close to 100 using individual hundreds boards (See Copymaster 2) to keep track of each person’s score. Collections of counting objects in packages of ten and individual ‘ones’ might also be used if needed to support some students.
Close to 100 is played in pairs with a dice (1-6). Players take turns to roll the dice and decide if the digit that comes up represents tens or ones. For example, if 5 is rolled it may be used as 5 or 50.
The player adds whatever they chose to their running total. That total is recorded each roll. Players have a total of seven rolls and must use all of these rolls. The player with the total closest to 100 after seven rolls wins. Players’ totals may go over 100. Here is an example: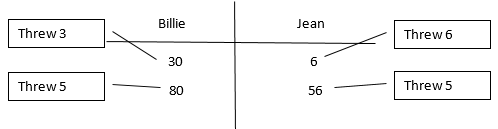
If appropriate, organise students into pairs or small groups to play this game. It can be adapted to the different knowledge in your class by changing the “close to” number (i.e. close to 10, close to 1000).
- After a few games, discuss winning strategies with the students. Some may suggest getting to 80 as fast as possible then choosing ones, or letting small digits represent tens and large digits ones. Discuss how the winner is decided if one score is less than 100 and the other is greater, e.g. 93 and 106. In that case 93 is ‘seven away’ from 100 and 106 is ‘six away’ so 106 wins.
- To cater for student differences, vary the game to backwards to zero from 100 (integers may arise) or using 3-digit numbers with each digit representing hundreds, tens or ones, aiming for 1000 with ten rolls.
Session Three
In this session students investigate how 100 can be partitioned to form ‘number buddies’ like 20 + 80 and 1 + 99.
Part One
- Introduce the students to the Slavonic abacus. An internet search for "Slavonic Abacus online" leads to many different interactive tools that could be used in the absence of a physical abacus. Each student should have their copy of the hundreds board and a transparent counter. Below is a Slavonic abacus showing 25 (left) and 75 (right).
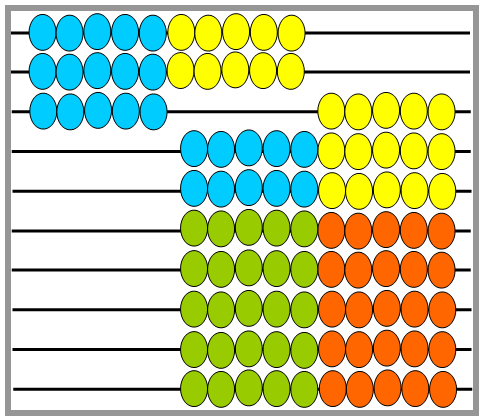
How many beads are in each row? How do you know?
How many beads are on the whole abacus (100)? How do you know? - Make blocks of beads by moving across whole rows of tens and some ones. Students put their counter on the matching number on their hundreds board. Discuss the structure of the number (tens and ones) and the way the number is written. To move beyond counting tens and ones verbalise the structure of the block of beads as you create it.
Eight tens and six ones, No tens and nine ones, five tens and two ones. - Develop imaging by masking the Slavonic abacus (turning it around or hiding it) and just saying the structure while creating the block of beads.
I’ve got seven tens and four ones. Move over 100 to see how the students react. Look for them imaging where the counter might go below the hundreds board.
I have 12 tens and five ones (125) - Next, work on different names for 100. Make 100 with place value material and then model various ways to split the 100. Each time a new split of 100 is made, invite students to show that split on the abacus.
- Ask another student to record an equation for the split and a number story to go with it. Model this, making explicit links to cultural contexts and learning from other curriculum areas that are relevant to your learners. See below for an example. See below for an example.
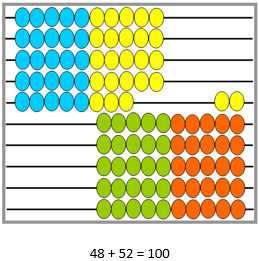
Number story:
On day 1 the community planted 48 trees that had been delivered by the council. On day 2 the local marae offered 52 native trees for planting. Altogether 100 trees were planted.
Or: 36 + 17 + 26 + 21 = 100 (36 + 64)
At the local beach, when the tide was down, Aniwa and her cousin collected 36 cockles. The next time they went collecting cockles Aniwa found 17, Rei found 26 and Kori managed to get 21. Over two days they had collected 100 cockles.
Part Two
- Play the game Number Buddies to 100 with calculators and the sets of tens and ones groupable objects students created in lesson one. Start with the Slavonic abacus. Move across a block of complete tens and ones. For example:
I have seven tens and two ones. How many beads is that? (72) - Point to the remaining collection of beads (not moved).
How many are left over here? How do you know? (28 - There are two tens and eight ones) - Try to highlight non-counting strategies, e.g. There are eight because 2 + 8 =10.
- Show the students how Number Buddies to 100 is played in pairs with a calculator. One player enters a two-digit number. Get a student to do this on the IWB calculator or with a simple online calculator. Make a block on the Slavonic abacus of that many beads. Say the first player keyed in 46.
The other player must add on the correct number to that number to make the total 100. Highlight that this involves thinking about what is left from 100 using the abacus. So if correct the other player would key in + 54 = and the calculator would display 100.
The game can be played competitively in pairs with a point awarded for each correct answer (best of ten tries). Get the students to record their work with equations, e.g. 46 + 54 = 100. - After playing the game for a while, ask the students to think about patterns that allow them to work out the “number buddies”. They might note that numbers where the ones digit is zero are easy, e.g. 40 + 60 = 100, as the tens digits need to add to ten (ten tens make 100). The other examples are more difficult, e.g. 39 + 61 = 100, as the tens digits add to nine and the other ten comes from collecting ones.
- Note: More advanced students might play Number Buddies to 1000. Students who are still developing their knowledge of numbers to 100 might benefit from playing Number Buddies to 10, 20, or 50. Consider the addition-facts knowledge of your students, and adapt the game in reflection of this. Alternatively, you could play Number Buddies to 100 with a small group of students, whilst others play Number Buddies to 1000 etc. Ultimately, you should support all students towards working with 100.
Session Four
In this session the students explore different names for the same two-digit number.
Part One
In the last lesson the class explored how 100 can be renamed in lots of ways. In this lesson, we explore the same concept with other numbers.
- Use place value equipment to model how 75 can be renamed as 6 tens and 15 ones or as 5 tens, and 25 ones. Joke about the funny names that are created, ‘Sixty-fifteen’ and ‘Fifty-twenty-five’. Record the pattern of names:
- 7 tens and 15 ones
- 6 tens and 25 ones
- Ask what would come next in the pattern.
What would happen to the beans to get the next name for 75? (A bag of ten would be shifted into the ones place)
If we kept the pattern going, when would it end? (75 ones) - Model 2 tens and 43 ones so the number showing is 63. Replace 10 ones with 1 ten, and repeat. This leads to a pattern of:
- 2 tens and 43 ones
- 3 tens and 33 ones
- 4 tens and 23 ones
- At each new movement of beans ask the students to predict the outcome and the new name for 63.
- Send the students off to practise renaming a two-digit number in pairs. Some may need their materials for Session One and some will be able to rename numbers without support. After a short period of practice, bring the class together to see if the students have understood the idea. Create a model of 5 tens, and 28 ones in the centre of the mat using your place value mat from Session Two.
What is this number? ‘fifty– twenty-eight’ or 78
What other names for that number can you find? ‘sixty-eighteen’, ‘seventy-eight’ but don’t forget ‘forty-thirty eight’, ‘thirty-forty-eight’.
Part Two
- Introduce the game of Cover Cathy Crocodile. This game is an adaptation of a game created by Joan Paske who was a prominent figure in New Zealand Mathematics education in the 1970s and 1980s. The game is in honour of her extensive contribution.
In the game students choose cards to cover the crocodile numbers of their board. The cards provide many options for covering numbers but most options involve renaming. For example, if a student wants to cover 72 they could do so by nominating:- 7 tens and 2 ones from the □ tens and 2 ones card
- 6 tens and 12 ones from the 6 tens and □ ones card
- 3 tens and 42 ones from the 3 tens and □ ones card
- There are many other options. Some students may need support with materials though it is hoped they can do the renaming mentally. Look for the following:
- Do your students fluently work between tens and ones?
- Can your students check that a card nominated by another player is viable?, e.g. 2 tens and 36 ones is a name for 56
- Do your students write numerals to support them?, e.g. Checking 74 by writing 40 + 34
- Let the students play the game until winners emerge. Gather your students together to discuss the thinking involved in the game.
When might renaming two-digit numbers be useful? Examples might include having ten dollar notes and one dollar coins and trying to find out how much money you have in total. - Pose this problem. Build 63 on the place value mat with groupable materials where all the students can see.
Suppose I have 63 toys. I give 26 of them to my brother or sister. How many do I have left? - Let students suggest ways to solve the problem. It is easy to allocate 20 packets of ten leaving 43 toys.
How many toys do we still need to take away? Can we rename 43 so it is easy to take away the other six toys? - Hopefully students suggest that a packet of ten toys can be broken up to change 43 into 30 and 13. Then the six toys can be removed leaving 37 toys. This task is a good indicator of whether students can apply renaming in a more difficult context of subtraction. You might change the numbers in the toy problem to give them a chance to practise renaming and subtracting.
Session Five
In this session students apply the place value structure of two-digit numbers to change a given number into a different number either mentally or with support of materials.
Part One
- Make the number 30 with grouped materials from Lesson One (3 tens) using the place value mat (Copymaster 1). Show the online calculator with 30 in the display.
Suppose I am set the challenge of changing from 30 to 80. What could I do? Is there a single operation I could key in? - Act on suggestions by students. Key in their suggestions and have a student change the object model to match. Students might suggest adding 50 to 30, like 50, 60, 70, 80 (skip counting in tens). Remind them that they can use basic facts with tens, just like they do with ones. If 3 + 5 = 8, then 30 + 50 = 80 since the units added are tens. They could also use the Slavonic Abacus to show this.
Suppose I am set the challenge of changing 80 to 10 in a single operation. What might I do? - Again mirror the calculations on the calculator with physical manipulation of the objects model. Look for students to recognise that if 8 – 7 = 1 then 80 - 70 = 10 since the units are tens.
- Next form 15 with the materials and enter 15 into the calculator.
This time I have to change 15 into 46 with one operation. What can I do? - This problem is more complex since it involves working with tens and ones. Invite suggestions from students and manipulate the materials as well as keying in the operations. Look to see if the students recognise the changes in the digits from 15 to 47 and what that means for the quantity to be added.
If I write 15 + □ = 47 does that help you work out what to do? - Some students may see that the tens digit has increased by three and the ones digit has increased by two. So the number added is 3 tens and 2 ones (32).
- Pose similar problems but increase the difficulty by following the sequence below. Watch to see how students cope with the change in re-unitising demands of the problems. Record each problem as a change unknown equation, e.g. 78 - □ = 45, to see if students link the value of the digits to the solution.
- Change 78 into 45
- Change 43 into 81
- Change 62 into 26
Part Two
- Ask the students to play the change game in pairs. Each pair will need a calculator and possibly a set of groupable objects from Lesson One if they need more support.
Players take turns to enter a starting number, say 34, and pass over the calculator with a change instruction, say “Change 34 into 88 with one operation.” Restrict the numbers to two places though moving to 3 digits is a significant extension for more competent students. A player gets a point for every correct change they give. The asker gets a point if the suggested change is incorrect. Look for the following:- Do the students use the place value of the digits in deciding what change to try?
- Do they recognise what digits need to change?
- Do they notice when a ten needs to be created or partitioned? e.g. 58 + □ = 92 or 73 - □ = 29
- After a suitable period of playing, bring the students together on the mat.
What did you do to make the problems harder for your partner? - Look for students to explain that the hardest challenges required both digits to change and that problems were hard if renaming was involved, particularly subtraction.
- For assessment of students’ understanding of place value, ask them to solve the problems on Copymaster 5. That will give you valuable data about their control over re-unitising tens and ones.
Dear parents and whānau,
Our next mathematics unit is based on Place Value. So we will be working a lot with two-digit numbers like 26 and 79. We will be using materials grouped in tens so we can make sense of the quantities that the numbers represent. For example, 62 means 6 tens and 2 ones and is said as “Sixty-two.”
We will also rename the two-digit numbers in flexible ways so that we can apply renaming to the operations, particularly addition and subtraction. Ask your child to discuss the strategies we are learning and explain their thinking.