This unit supports students in developing an understanding of three-digit numbers and how to operate with them.
- Represent three digit whole numbers using numerals, words and materials.
- Count in ones, tens and hundreds from a given three digit number.
- Find the difference between two three digit whole numbers.
- Use place value units of hundreds and tens to make estimates of the number of people in a crowd.
Understanding place value is crucial if students are to develop the estimation and calculation skills necessary to become numerate adults. Our number system is based on groupings of ten. Ten ones form one ten, ten tens form one hundred, ten hundreds form one thousand. And so the system continues to represent very large numbers. The place values, one, ten, one hundred, one thousand, etc., are powers of ten. Therefore, although our number system is sophisticated, it may not look it. While numbers are present around us in various environments, the meaning of digits in those numbers, and the quantities they represent, can be challenging to understand.
To represent all the numbers in our system we use just ten digits, 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. The word for digits also comes from our fingers. We don’t need a new number to represent ten because we think of it as one hand (one group of ten). Similarly when we add one to 999 we write 1000 and do not need a separate symbol for one thousand.
The position of the 1 in 1000 tells us about the value it represents. Zero has two uses in the number system, as the number for ‘none of something’, e.g. 6 + 0 = 6, and as a place holder in a number like 7040. Place holder means it occupies a place or places so the reader knows the values represented by of the other digits. In 7040 zero is acting as a place holder in the hundreds and tens places.
Place value means that both the position of a digit as well as the value of that digit indicate what quantity it represents. In the number 753 the position of the 7 is in the hundreds column which means that it represents seven hundred. Five is in the tens column which means that it represents 5 units of ten, 50.
Renaming a number flexibly is important. In particular it is vital that students understand that when ten ones are created they form a unit of ten, and when ten tens are created they form a set of one hundred. For example, the answer to 210 + 390 is 6 hundreds since one ten and nine tens combine to form another hundred. Similarly when a unit of one hundred is ‘decomposed’ into tens the number looks different but still represents the same quantity. For example, 420 can be viewed as 4 hundreds and 2 tens, or 3 hundreds and 12 tens, or 2 hundreds and 22 tens, etc. Decomposing is used in subtraction problems such as 720 – 480 = □ where it is helpful to view 720 as 6 hundreds and 12 tens.
Place value was devised to count large numbers of objects and represent the set of objects using a succinct set of numerals. It is appropriate that students learn to use place value as a means to estimate the number of objects in a set and count the number exactly.
Sessions One and Two
In these session students explore counting sequences, particularly with tens and ones. They come to understand why numbers can change considerably with the addition of one or ten, especially when ten units of a particular place are made and those ten units form a unit of the next highest place value. For example, if ten is added to 393 the nine tens become ten tens and are renamed to form another hundred. So, 393 + 10 = 403. Zero plays a critical role as the numeral for ‘nothing of something’ and as a place holder in numbers like 403.
Understanding the patterns of change in digits as numbers are renamed is important for mental calculation. For example, if tens are added to 403 to pattern of sums is 413, 423, 433,.. Only the tens digit changes until 493 is reached. Students need to recognise situations when adding one unit of a given place value changes only the digit in that place, and when renaming will occur and two or more digits will change, e.g. 493 + 10 = 503.
Sessions Three and Four
Number sense requires students to have an understanding of the quantities that numbers represent. In these sessions student organise materials to represent three digit numbers. Non-proportional representations of place value like money and the traditional abacus can give students an impression that the digits in the tens and hundreds places are just units of one. Since the place values are powers of ten, meaning one hundred is ten times more than ten (and so on), the quantities represented by the place values scale rapidly. Models for place value where ones are visible is essential for students to appreciate the true value of digits in numbers.
In these sessions student create a physical model for three digit numbers and use place value units as a powerful way to estimate and count the number of people in a crowd. In doing so they appreciate the elegant power of grouping ten ones as a unit of ten, and ten tens as a unit of one hundred.
The learning opportunities in this unit can be differentiated by providing or removing support to students and varying the task requirements. Ways to support students include:
- modelling the use of arrow cards, place value materials, and calculators
- varying the complexity of the numbers used in each activity
- providing opportunities for individual, grouped, and paired work
- strategically organising students into pairs and small groups in order to encourage peer learning, scaffolding, and extension
- working alongside individual students (or groups of students) who require further support with specific areas of knowledge or activities. The independent challenge tasks can provide opportunities for revisiting specific concepts with groups of students.
To increase the relevance of this unit, the questions posed can be adapted to reflect the interests, experiences, and cultural backgrounds of your students. You could also encourage students ready for extension to create word problems that reflect a shared, relevant context and the mathematics introduced in the session. In turn, these problems could be used as practice tasks for the rest of the class.
Te reo Māori kupu such as uara tū (place value) and tatau (count) could be introduced in this unit and used throughout other mathematical learning.
You could also encourage students, who speak a language other than English at home, to share the words related to place value from their home language.
- Dice, scissors, calculators, glue sticks, A3 paper
- Copymasters One to Seven (links at bottom of unit).
- PowerPoints One and Two (links at bottom of unit).
Use Copymaster One to make a laminated version of Place Value People. Create units of one hundred, tens and numbers one. You need around 20 of each unit.
Use Copymaster Four to make an A3 sized version of The Thousands Book. This could be in colour, laminated and secured with a book ring through the top left corner of each page.
Session One
In this session students investigate the place values of three digit whole numbers. They relate the numerals to the quantities they represent using photocopied sheets of Place Value People (see Copymaster One).
Whole Class Introduction
- Use the Place Value People and a place value mat (drawn on a piece of A3 paper) to model a range of different three digit numbers.
- For each number, ask your students to write the numeral for the number of people and to practise with a partner how to say the words for that number.
- Model counting on in ones and tens until that place is full and then replace the tens ones with a ten (or ten tens with a hundred).
- Write down the new number and read it out as you add each unit.
Some key ideas to discuss are:
- The place of a digit tells the size of the unit being counted and the digit represents the number of counts of that unit, e.g. In 247 the 4 represents four counts of ten;
- When a given place gets ten units in it, one unit of the place to the left gets formed, and added to that place, e.g. When 20 is added to 185 ten tens form a unit of one hundred, so one unit is added to the hundreds place to create 205.
Independent Challenge
Copymaster Two can be used to provide challenges for students with 3 digit numbers. All of the challenges involve combining place value units to form the next largest unit to the left.
Alternatively, students might work in pairs to set challenges for each other with a calculator, photocopied Place Value People, and scissors. For example:
- Student A enters 578 on the calculator
- Student B makes 578 with Place Value People materials on a place value mat (5 hundreds, 7 tens and 8 ones)
- Student A says “add forty” (The problem must require more than ten units to be in at least one place value column)
- Student B adds 4 tens and combines 10 tens to make 1 hundred. They move the new hundred to its correct place to form 618, say the new number in words, e.g. “six hundred and eighteen”, and confirm the result by adding 40 on the calculator (578 + 40 = 618).
Reflection
It is important that your students move beyond manipulation of the Place Value People to anticipation of the result. Discuss how they might know the answers to these problems without having to work with the materials (see Copymaster Three). You might check their predictions with a calculator.
- “Moa is a small town that has 196 people living in it. A family of six people move into Moa. How many people live there now?”
- “Awarua has 852 people living in it. A new factory starts up and 60 new people come there to live. How many people live in Awarua now?”
Session Two
In this session the students consolidate the connection between the place value of two digit numbers and the quantities that the numbers represent.
Whole Class Introduction
- Introduce the Thousands Book (See Copymaster Four). This book can be used in many ways to practise counting in different units. Counting practice is more effective if the model of quantity (Place Value People) is used alongside the numerals and words.
- Adding one to a number is represented by a slide of one space to the right and subtracting one is represented by a slide of one space to the left. Adding ten to a number is represented by a downward slide of one space. The inverse of adding ten, subtracting ten, is represented by an upward slide of one space. Adding one hundred is represented by going down one page and the inverse, subtracting one hundred, is represented by going up one page.
- Use the Thousands Book to model a sequence of adding tens. Place a counter on 243, and then move it down one row at a time. Make the quantity for the number the counter rests on each time using Place Value People. Students will quickly recognise the easy way to add ten rather than build the number from scratch. At the addition of ten onto 293 ask the students to predict the next number in the pattern (303). Note the renaming of ten tens as one hundred that will be needed in the Place Value People model. Then the counting sequence continues as before.
- Model the same process for a sequence of adding hundreds. Start at 9, and move forward one page at a time. When 100 is added to 909 students will need to anticipate the next page on the book, 1001 – 1100.
- Counting operations on the Thousands Book might be practised each day for a period of 10-15 minutes. Copymaster Five is a set of cards that can be used to pick operations randomly from a selected starting number.
Independent Challenge
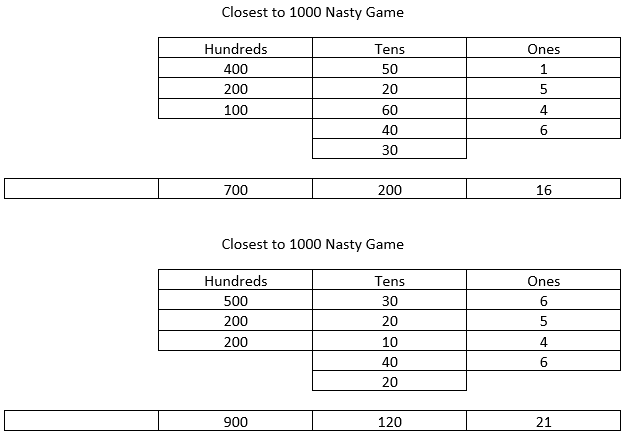
The ‘Close to 1000 Game’ is a variation on ‘Close to 100’ which was introduced in “Place Value Tens and One”, the first unit in this Place Value series. Play the game in threes to create interesting dynamics.
Each trio will need one dice (1-6), photocopied Place Value People they can cut up if need be, and a calculator. They will need to keep track of their score using Copymaster Six.
Players take turns to:
- Roll the dice, e.g. 4 is rolled
- Choose whether the number showing represents 4 ones, 4 tens or 4 hundreds
- Either add that number to their score or fill the number in another player’s scoresheet but only if it is tens or ones, e.g. 40 and 4 can be given but 400 cannot
Each player can only have twelve rolls of the dice. So if the twelve spaces of their scoresheet are full from numbers given by other players they must give the next numbers they roll to other players. Note that there are four spaces for ones, five spaces for tens and only three spaces for hundreds on the scoresheet.
At the end of ten rolls for each player the person with the total closest to 1000 wins. So a score of 1236 beats a score of 698 because it is 236 away for 1000 while 698 is 302 less than 1000. People materials can be used to build up the totals physically if needed and the calculator used to check mental calculations by the students.
Reflection
Close to 1000 gives the students the opportunity to combine hundreds, tens and ones. Ideally the students should calculate mentally rather than with reliance on materials or a calculator. Discuss how they might add up players’ totals. Here are a couple of examples:
Who has won the game?
The winner is decided by difference from 1000. What does difference mean?
How can the difference be worked out?
Session Three
In this session students use the People Materials to show interesting 3 digit whole numbers. In doing so they gain a sense of the quantity that the numbers represent. They also begin to use place value to find the difference between quantities represented by three digit numbers.
Whole Class Introduction
Show the students the interesting facts chart (PowerPoint One). Ask the students to work in pairs to make the number of people shown on each slide using photocopied people sheets. Choose slides that you think will appeal to your students and make three of four of the numbers. You may need to check on the location of The Chatham Islands and Kawerau Gorge. Make sure the students make a place value chart of each number by lightly glue sticking the cut out people units to an A3 page.
Discuss ideas about the numbers, such as:
- What does the word average mean?
- What does ‘in every 10 000’ mean?
- Why is zero important in the numbers 602 and 370?
- Which number is the least? …the greatest?...closest to 500?
- How many tens are in each number? Note that hundreds contain tens, so in 886 there are 88 tens.
Independent Challenge
- Pose the problem: Suppose I wanted to know how many more New Zealanders fly overseas than are born each day. How would I do find that out?
This problem is about the difference between 163 and 886 which can be found by either adding on from 163 to 886 or subtracting 163 from 886. These operations can be recorded as:
163 + □ = 886 or 886 – 163 = □. - Let the students work out their answer to the problem in pairs. They made a People Materials model of each number in the whole class time so they should use the same model to work out the difference. Look for students to:
- Use the materials if necessary to check the validity of their answers.
- Use the hundreds, tens, and ones units to make finding the difference easier. Counting in ones is cumbersome in this case.
- Realise that hundreds, tens and ones units can be treated like any other unit. For example, 800 – 100 is like 8 – 1 = 7 in hundreds, so the answer is 700.
- If they choose adding on to 163 encourage students to ‘bridge’ to the nearest place value unit, decades and hundreds. For example, 163 + 7 = 170, 170 + 30 = 200, etc.
- Look for students to use symbols and empty number lines as a way to record their calculations,
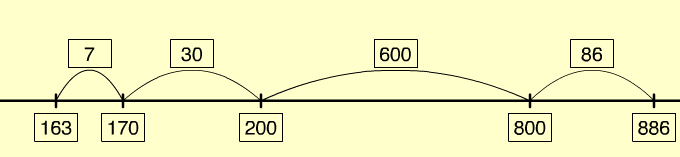
- Consider the efficiency of adding on (less efficient in this case) and subtracting.
- Students who complete the problem quickly can be asked to find the difference between two other three digit numbers. Is the same method still the most efficient?
- After an appropriate time bring the class together to discuss the bullet points above. You may find that students need another lesson on finding differences. This skill is a fundamental application of place value.
Session Four
In this session the students use place value to estimate the number of people in a crowd and to count the number of people exactly.
Whole Class Introduction
- Show the students the first slide of PowerPoint Two.
How many people are going to the rugby game? How could we find out? - Students might suggest many possible strategies, such as:
- Count by ones (What problems might we have doing that?)
- Count the colours separately
- Draw around groups of people (What sized group should we use? Why?)
- Click the mouse to get the first animation. A rectangle surrounding ten people will appear in the top right corner.
How many people are in the rectangle? - How could we use this rectangle to estimate the number of people in the whole crowd? (Look for students to imagine an array of columns and rows of the rectangular unit). Click to reveal a top row and right column of the array.
Do students suggest that 5 x 5 = 25 rectangles will fit over the whole crowd, and 25 tens are 250 people? - Discuss what is meant by an estimate (An approximate answer that can be found more quickly than counting exactly).
Will our estimate be exactly right?
What might cause it to be a bit incorrect? (Students might recognise that each rectangle of that size will not always hold exactly ten people and that some people are part of two or more rectangles)
How might we change our method so it is more accurate? (Students might suggest that most rectangles hold more than ten or that a curved unit of ten might be better) - Slides 2 and 3 of PowerPoint Two show exact units of ten being created and marked off as they are counted. The crowd has 28 units of ten with two extra people.
How many people is that altogether? (Look for students to use their knowledge that ten tens are one hundred).
Independent Challenge
- Copymaster Seven provides another crowd. Challenge the students to work in pairs to first estimate the number of people in the crowd, explaining their method of estimation, then find a way to use place value to count the number of people exactly.
- Provide copies of Copymaster Seven to work on. After a suitable period of time gather the class to discuss their methods.
- Slide 4 of PowerPoint Two shows part of the crowd organised into tens.
What is a reasonable estimate based on this partitioning?
Based on a unit of one hundred, four hundred is a reasonable estimate.
Based on a unit of ten organised into a 6 x 7 array, 42 tens or 420 is a reasonable estimate. - There are actually 485 people in the picture.
Session Five
- To consolidate the ideas read your students this book:
Smith, D. J. (2011). If the world were a village: A book about the world’s people (2nd Edition). Toronto, Canada: CitizenKid (also available as a video online). - Students should use a one hundred sheet to represent the various continents, e.g. 61% of people are Asian but only 1% are Oceanian (NZ is part of Oceania).
- Provide challenges like:
If there were 1000 people, not one hundred, how many people would be from each continent? - Change 1000 to various numbers to provide greater challenge.
- Compare the makeup of the world to the makeup of your class.
Where were people in your class born?
What would the hundred people chart look like for your class?
Hello parents and caregivers
Our next mathematics unit is based on Place Value. We will be extending our knowledge of two digit numbers to include three digit numbers, like 403 and 279, and into the thousands. We will represent three digit numbers in different ways to get an idea of the quantities the numbers represent.
We will also rename the three digit numbers in flexible ways so that we can apply renaming to the operations, particularly addition and subtraction.