This unit supports students in developing an understanding of four-digit numbers and how to operate with them.
Session One
- Represent four digit numbers using Place Value People and as compact and expanded numerals.
Session Two
- Apply place value to change a four digit number to a target number by addition or subtraction.
Sessions Three and Four
- Rename four digit numbers in flexible ways.
Session Five
- Know the number of tens, hundreds, and thousands unit in four place numbers.
Understanding place value is crucial if students are to develop the estimation and calculation skills necessary to become numerate adults. Our number system is based on groupings of ten. Ten ones form one ten, ten tens form one hundred, ten hundreds form one thousand. And so the system continues to represent very large numbers. The place values, one, ten, one hundred, one thousand, etc., are powers of ten. Therefore, although our number system is sophisticated, it may not look it. While numbers are present around us in various environments, the meaning of digits in those numbers, and the quantities they represent, can be challenging to understand.
To represent all the numbers in our system we use just ten digits, 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. The word for digits also comes from our fingers. We don’t need a new number to represent ten because we think of it as one hand (one group of ten). Similarly when we add one to 999 we write 1000 and do not need a separate symbol for one thousand.
The position of the 1 in 1000 tells us about the value it represents. Zero has two uses in the number system, as the number for ‘none of something’, e.g. 6 + 0 = 6, and as a place holder in a number like 7040. Place holder means it occupies a place or places so the reader knows the values represented by of the other digits. In 7040 zero is acting as a place holder in the hundreds and tens places.
Place value means that both the position of a digit as well as the value of that digit indicate what quantity it represents. In the number 2 753 the position of the 7 is in the hundreds column which means that it represents seven hundred. Two is in the thousands column which means that it represents 2 units of one thousand (2 000).
Renaming a number flexibly is important. In particular it is vital that students understand that when ten ones are combined they form a unit of ten, when ten tens are combined they form a unit of one hundred, and when ten hundreds are combined they form a unit of one thousand. For example, the answer to 2 610 + 4 390 is 7 thousands since 610 and 390 combine to form another thousand. Similarly when a unit of one thousand is ‘decomposed’ into ten hundreds the number looks different but still represents the same quantity. For example, 4 200 can be viewed as 4 thousands and 2 hundreds, or 3 thousands and 12 hundreds, or 2 thousands and 22 hundreds, etc. Decomposing is used in subtraction problems such as 7200 – 4800 = □ where it is helpful to view 7200 as 6 thousands and 12 hundreds.
Place value was devised to count large numbers of objects and represent the set of objects using a succinct set of numerals. It is appropriate that students learn to use place value as a means to estimate the number of objects in a set and count the number exactly.
Specific Teaching Points
Session One
Writing four digit numbers in expanded form is a traditional place value task that can help students to calculate mentally and in written form. For example, 7 249 can be expanded to 7 000 + 200 + 40 + 9. It is also important for students to recognise which digits change when a given number is added to or subtracted from an existing number. For example, if 60 is added to 3 420 only the tens digit will change. However, if 60 is subtracted from 3 420 both the hundreds and tens digits will change since one hundred must be decomposed to create tens.
Session Two
The theme of digit change is more complex when students must determine the number to add or subtract, from a given number, to change it into a target number. For example, to change 567 into 607 the ones digit is invariant. The tens digit changes by adding four tens (40), which also causes the renaming of ten tens as one hundred.
Session Three
Renaming numbers in multiple ways is foundational to flexible calculation. The combining and decomposing of place value units means that a given number can have many names. For example, 456 can be represented as 4 hundreds, 5 tens and 6 ones. It is also 45 tens and 6 ones or just 456 ones. Some ways of renaming are particularly helpful. Decomposition of place value units is useful for subtraction. In the calculation 456 – 183 = ? treating 456 as 3 hundreds, 15 tens and 6 ones makes the subtraction very easy.
Session Four
The fundamental law of place value is that if ten units of one place are formed then a unit of the next highest place are created. For example, when 247 and 562 are combined ten tens are formed which creates another unit of one hundred. Similarly if a place value unit is partitioned it forms ten units of the place value next smaller to it. To calculate 819 – 30 = ? a one hundred unit can be decomposed to form ten tens, renaming the number as 7 hundreds, 11 tens and 9 ones. These rules for composition and decomposition of units can result in strangely appearing changes to numbers in counting sequences. For example, 970, 980, 990, 1 000, 1010, … and 3 004, 3 003, 3002, 3001, 3 000, 2999, 2998, …
Session Five
Nested place value is the idea that place value units are included in other place value units, for example, tens are within hundreds, and hundreds are within thousands. In real life an article costing $280 might need to be paid for in $20 notes. Knowing how many tens are in $280 (28 tens) is very helpful.
Understanding nested place value helps students to understand the scale of quantity represented by digits in a number. For example, in 5 658 there are two fives. However the five in the thousands place represents a quantity one hundred times greater than the five in the tens place. In real life, reading a contract price with understanding of the size of the numbers is essential.
The learning opportunities in this unit can be differentiated by providing or removing support to students and varying the task requirements. Ways to support students include:
- modelling the use of arrow cards, place value materials, and calculators
- varying the complexity of the numbers used in each activity
- providing opportunities for individual, grouped, and paired work
- strategically organising students into pairs and small groups in order to encourage peer learning, scaffolding, and extension
- working alongside individual students (or groups of students) who require further support with specific areas of knowledge or activities. The independent challenge tasks can provide opportunities for revisiting specific concepts with groups of students.
The context for this unit can be adapted to suit the interests, experiences, and cultural backgrounds of your students. For example, in session 5, the question "Civil Defence wants us to make teams of ten people to prepare for emergencies, like earthquakes or cyclones. How many teams could we make with 483?" could be adapted to reflect a current issue that is relevant to your students, their interests, and their learning (e.g. We need to organise our school of 283 students into groups of 10 for our elective classes. How many classes could we make). Although the problems presented in other sessions do not reflect any specific real-world contexts, you could encourage students ready for extension to create word problems that reflect a shared, relevant context and the mathematics introduced in the session. In turn, these problems could be used as practice tasks for the rest of the class.
Te reo Māori kupu such as uara tū (place value) and tatau (count) could be introduced in this unit and used throughout other mathematical learning.
You could also encourage students, who speak a language other than English at home, to share the words related to place value from their home language.
- Arrow cards
- Place Value People
- Place Value Chart printed to A4 and A3 sizes
- Place Value: Calculator change challenges
- Copymaster Four
- Copymaster Five
- Calculators
- PowerPoint
- Access to an online calculator
- Cover Cathy Crocodile (3 Digit Version) (a coloured laminated set of boards and cards for every group of five students in your class)
- Access to the Modeling numbers: 6-digit numbers learning object
- Place value materials (e.g. blocks).
Prior Experience
Students would benefit from working through these three easier units on place value prior to the introduction of this unit:
Session One
In this session students consolidate their understanding of three digit whole numbers and progress to four digit numbers. They learn to write numbers in expanded and compact form and apply place value to challenges in which they must change a given number to a target number.
Whole Class Introduction
- Model how to make 482 with arrow cards.
- Ask a student to make the number with Place Value People on a Place Value Chart (A4 sized)
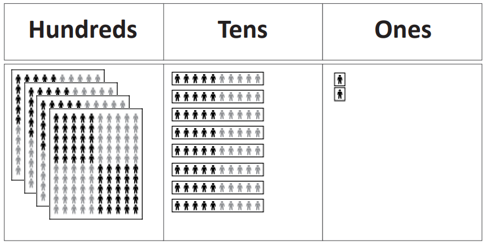
- Expand the arrow cards to show how the number is composed of 400 + 80 + 2. Ask students to indicate on the place value chart what quantity each digit is referring to.
How many ones are in 482 in total? (482)
How many tens are in 482? (48)
Where are those tens on the place value mat? (40 tens are in 400)
- Ask students: Imagine I entered 482 in a calculator and wanted to change it to 502 without clearing. What operation might I use? (adding two tens (20) gives ten tens which are renamed as one hundred and transferred into the hundreds column, giving five hundreds and two ones. You may like to use a calculator to show the operation. Ask a student to show how 482 becomes 502 using the Place Value People.
- Create similar problems with different numbers such as:
739 + 1 = 740, 275 + 30 = 305, 264 + 36 = 300
- Model each operation with arrow cards and Place Value People. You might go into four digit examples, e.g. 3 571 + 30 = 3 601. Ten pages of one hundred people are easily clipped together with a paper clip to form thousands.
Independent challenge for students
For this game, students work in teams of three. Each group needs a set of arrow cards. The game can be played with a full set of thousands, hundreds, tens and ones cards or the challenge can be reduced by playing with just hundreds, tens and ones cards.
The instructions here are for the easier game. For each round the cards are shuffled and dealt equally so each player has three hundreds cards, three tens, and three ones cards. For each round there is a target clue (See the PowerPoint), such as “Between 300 and 600” or “Within 50 less or greater than 700” or “Rounds to 300”. The players build numbers to satisfy the target. They can only build three numbers so the maximum number of points is three each round. No card can be used twice in a round.
At the end of Round Ten the player with the most points wins.
Reflection
- Pose this challenge to your students.
You have these arrow cards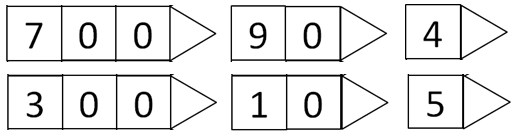
What numbers is it possible to make with these cards?
- Look for students to approach the task systematically. Motivate them by saying that you think only eight numbers can be made (This only includes the 3 card combinations).
- You might ask the students to investigate the problem in their groups or discuss it as a whole class.
- You might use a tree diagram to organise the possible numbers made from three cards.
- Twelve numbers can also be made using two arrow cards (790, 710, 704, 705, 390, 310, 304, 305, 94, 95, 14, 15) and the cards on their own form another six numbers (700, 300, 90, 10, 4, 5).
- You might challenge the students to make as many numbers as they can with a different set of cards. Obviously increasing the numbers of available cards increases the difficulty as does have different numbers of hundreds, tens, and ones cards, or including thousands cards.
Session Two
In this session students explore renaming of three numbers in multiple ways. Flexibility in renaming is essential to mental and written calculation with any set of numbers, but is particularly important with whole numbers that form the basis of other sets, such as integers and rational numbers.
Whole Class Introduction
Calculator change games are a useful way for students to apply their understanding of place value. The difficulty of a particular change is a combination of the number of digits that need to change and the re-unitising of place value units required. For example, changing 435 to 495 is relatively easy since only the ten digit changes by six units of ten (60) and no re-unitising is required. However changing 435 to 395 is considerably more difficult as both the tens and hundreds digits change and one hundred needs to be re-unitised as ten tens.
- Use an online basic calculator and enter the number 435. “In this challenge I need to change 435 to 495 by adding or subtracting one number. I cannot clear the calculator and just enter 495. How could I do that?”
- Ask a student to make 435 with Place Value People on a place value mat then invite ideas of how to change the number to 495. When students offer a suggestion, use the calculator to confirm whether the idea works or not. Also carry out the operation with Place Value People to see what is occurring with the quantities the numbers represent.
- Pose a series of challenges, all starting with 435:
- Change 435 into 515
- Change 435 into 405
- Change 435 into 395
- Change 435 into 488
- Change 435 into 409
Independent challenge for students
The Place Value: Calculator change challenges provides a series of calculator change challenges that increase markedly in difficulty. Allow the students access to calculators and photocopied Place Value People so they can experiment with different operations.
You may decide to let students work in pairs or as individuals, depending on your assessment purposes. Look for students to:
- Notice which digits change between the starting number and the target number
- Associate those digit changes with the place values involved
- Recognise when re-unitising is needed, e.g. ten tens make one hundred or one hundred is broken done into ten tens
- Calculate the number of units required for the change using basic fact knowledge, e.g. 236 → 286 involves adding five tens using 3 + 5 = 8
Reflection
It is worthwhile to work through some of the challenges students find difficult, as a class, to support students in validating their ideas. Ideally, choose examples where re-unitising is required.
For example:

In this case both the tens and hundreds digits change. The operation is subtraction since the target number is less than the starting number. So to find the required operation, one hundred must be re-unitised, into ten tens. Actually it is easiest to see 217 as twenty-one tens and seven ones and find the answer using the difference between 21 and 18 (3 tens). 217 can be renamed as ‘one hundred and eleventy-seven’ and written as 211 7. This renaming can be shown by making 217 with Place Value People on the place value chart, cutting on hundred into ten tens, and moving those tens into their correct place. Then three tens (30) can be removed to make 187.
Session Three
- Begin with the number 1 11 7 (one hundred and eleventy-seven) which is made up of one hundred, eleven tens and seven ones. This should be familiar to students from the previous lesson.
What is the usual name for this number? (217)
Where does the second hundred come from? (Combining ten tens)
- Make the number 4 6 15 (four hundred and sixty-fifteen).
What is the usual name for this number? (475)
Where does the other ten come from? (ten ones)
- Make four hundreds, twelve tens and seventeen ones (4 12 17)
How might we say that number? (Four hundred, twelve-ty seventeen)
What is the usual name for this number? (5 3 7)
How does it become 537?
Show how ten ones combine to make ten, and ten tens combine to make one hundred.
- Model of 529 made with Place Value People on a place value chart.
What is this number?
What interesting other names can you create for the same number?
Let the students discuss possible names in pairs and record their ideas.
Possible names include:
529 ones, 4 hundreds 12 tens and nine ones, 5 hundreds 1 ten and 19 ones, 52 tens and 9 ones, 42 tens and 19 ones,… etc.
You might create a chart of the possible names for 529 with Place Value People models to represent those names.
Ask the students to confirm each suggestion by showing how the model of 529 can be re-unitised to form the new name.
Independent challenge for students
Provide the students with copies of Cover Cathy Crocodile (3 Digit Version). You will need a coloured laminated set of boards and cards for every group of five students in your class. The activity can be set as a co-operative challenge to cover all the crocodiles or as a competitive game. Student will need to play the game several times to gain fluency in renaming three digit numbers.
Reflection
Take particular cards from the Cover Cathy Crocodile set and ask what numbers might be covered with that card. For example, the card 6 hundreds □ tens and 9 ones can be used to cover the sequence of numbers; 609, 619, 629, 639, …, 699, 709, 719, …
Session Four
In this session students extend the number system to four digit numbers. They use Place Value People models to show how ten hundreds combine to form one thousand and the inverse operation of partitioning one thousand into ten hundreds.
Whole Class Introduction
For this session you will need photocopied Place Value People models for the students to use and staplers to combine hundreds into thousands. Use A3 sized place value charts.
Show the students a ‘book’ of ten hundreds stapled in the top left corner.
How many people are in this collection? What clues do you need to find that out?
Students should ask how many hundreds are in the collection (ten) and give one thousand as the total number of people. Use thousands together with other Place Value People units to form the quantities and ask the students to write numbers and words for those quantities. It is important to include zeros as place holders in some of the numbers.
Independent challenge for students
For this activity students should work in pairs or threes. Copymaster Four has a set of questions based on the number of residents living in Whangamata township (you could adapt this to reflect your local area). Students need to build the numbers using Place Value People and use the model to check their answers at each change in the number of residents. Insist that students record their answers to each question and justify how they know the number is correct. Early finishers can make up some other scenarios to change the population of the town.
Look for your students to:
- Recognise which digits are likely to change as a number of people is added or subtracted from the population
- Recognise when units of one, ten, and one hundred will be combined to form a unit of the next highest place value
- Show how larger place value units can be partitioned to forms smaller units, particularly thousands partitioned to form ten hundreds and hundreds partitioned to form ten tens
Reflection
- Make the number 4 000 using Place Value People on a place value mat.
How many people would be left if only one person left this town?
Use a calculator to check students’ predictions (4 000 - 1 = 3 999)
Why do all the digits change when only one has been taken away?
Model the process of subtraction.
- Make the number 2 400 using Place value People on a place value mat
How many people would be left if ten people left this town?
Which digits will change? Why?
Model the process.
- Pose this problem for students to answer without any support.
There are 5 067 people in a town. 100 people leave. How many people are left?
Session Five
In this session students apply their understanding of four digit numbers. They use Place Value People models to show how many hundreds, tens and ones are ‘nested’ in a four digit whole number.
Whole Class Introduction
- Make the number 483 with Place Value People.
Civil Defence wants us to make teams of ten people to prepare for emergencies, like earthquakes or cyclones. How many teams could we make with 483?
Look to see if your students can identify that there are 48 tens in 483 (40 in 4 hundreds and 8 in 8 tens or eighty).
- Change the number of people to 1 275 are ask how many teams of ten can be formed.
Look to see if your students identify that there are 127 tens in 1 275 (100 in 1 thousand, 20 in 2 hundred, and 7 in seventy). You may need to partition one thousand into hundreds and then into tens physically to support some students.
- Ask the number of tens in 3 709, being aware that the zero may cause confusion. Model the number if necessary with Place Value People.
- How do we write finding the number of tens in 483?
You may need to relate that problem to “How many threes are in twelve?” for your students to link the problem to division. Aim to record division equations and use a calculator to confirm the answers:
483 ÷ 10 = 48.3
1 275 ÷ 10 = 127.5
3 709 ÷ 10 = 370.9
- Ask the students what they notice. Some may see that the whole number of tens is given by the digits to the left of the ones place and the remainder is the ones digit.
What will happen if we divide by one hundred instead of ten?
483 ÷ 100 = 4.83
1 275 ÷ 100 = 12.75
3 709 ÷ 100 = 37.09 - What are these answers actually telling us? (The number of teams of one hundred that can be made from a number of people) You may need to model finding how many hundreds are in 3 709 with Place Value People as an example.
Independent challenge for students
Copymaster Five has problems about identifying the number of tens and hundreds in a given number. The problems increase in difficulty. Some students will need Place Value Materials to attempt the problems but many will be able to solve the problems using symbols with understanding. Ask your students to check their answers using division, e.g. “How many tens are in 8 095?” can be checked with 8 095 ÷ 10 = 809.5
Reflection
- To assess your students’ ability to transfer their place value understanding, to a new representation, go to the Modeling numbers: 6-digit numbers learning object.
- Make the numbers using the place value block representation then ask students to anticipate the result of the operations.
2 000 – 1 = ?
The result is an animation of the partitioning of one thousand and progresses through to the ones place.
- Appropriate challenges include:
4 796 + 10 = ?
3 500 – 10 = ?
9 000 – 10 = ?
7 047 – 100 = ?
4 899 + 1 = ?
6 204 – 10 = ?
Hello parents and caregivers
Our next mathematics unit is based on Place Value. We will be extending our knowledge of three digit numbers to include four digit numbers, like 7 403 and 2 579. We will represent four digit numbers in different ways to get an idea of the quantities the numbers represent.
We will also rename the four digit numbers in flexible ways so that we can apply renaming to the operations, particularly addition and subtraction.