This problem solving activity has a number and algebra (equations and expressions) focus.

It is 30 cm long.
He plays with it and makes different shapes.
He thinks that the rectangle with the biggest area that he can make, is a square.
His sister Miri disagrees.
Who is right and why?
- Determine the maximum area of a rectangle with a given perimeter.
- Consider how the area of a quadrilateral changes as its shape changes.
- Interpret a relationship from a graph.
This is the same problem as in Peter’s Second String, Measurement, Level 5.
However, at this level, students are expected to have a more sophisticated way to solve the problem. To do so, students need to be able to measure lengths and calculate the perimeters and areas of rectangles using the formulae: perimeter = twice length plus twice width and area = length x width. In addition, it would help if they have already used tables to solve Peter’s Second String, at Level 5.
Note: The extension for this problem, involving a conjecture about any quadrilateral, is challenging.
There are seven problems related to perimeter and area.
The first set includes: Peters’ String, Measurement, Level 4; Peters’ Second String, Measurement, Level 5; Peters’ Third String, Algebra, Level 6; The Old Chicken Run Problem, Algebra, Level 6; and the Polygonal String Problem, Algebra, Level 6. These show the non-link between rectangles’ areas and perimeters, including showing that among all quadrilaterals with a fixed perimeter, the square has the largest area. The final problem that looks at the areas of regular polygons with a fixed perimeter and shows that they are ‘bounded above’ by the circle with the same perimeter.
The second set includes: Karen’s Tiles, Measurement, Level 5 and Karen’s Second Tiles, Algebra, Level 6. These problems explore maximum and minimum perimeters for a given area.
Mathematics is more than doing calculations or following routine instructions. Thinking and creating are at the heart of the subject. Though there are some problems that have a set procedure or a formula that can be used to solve them, most worthwhile problems require the use of known mathematics (but not necessarily formulae) in a novel way.
- Copymaster of the problem (English)
- Copymaster of the problem (Māori)
- ruler
- pieces of string of various lengths
- squared paper or graph paper
The Problem
Teaching Sequence
- Introduce the problem to the class and discuss with the students approaches they might use.
- Have students investigate Peter’s conjecture in any way that they want, although encourage more sophisticated approaches. As they record equations, assist if necessary
- As they work, check on their progress. Encourage them to set up some equations and reduce the number of dependent variables to one.
- If a number of students are struggling, have a brainstorming session.
- Share the students’ answers. Have them record their solutions and ensure that they have carefully explained their arguments.
- Encourage students to try the Extension Problem. Give them time to think about it.
Extension
If Peter made any quadrilateral shape with his string, would the maximum area he could get be produced by a square?
Solution
We have already done this problem using a table in Peter’s Second String, Level 5.
At this level, however, students should be encouraged to see how to use algebra more effectively in such problems.
What do we know? If we make Peter’s string into a rectangle with side lengths L and W, then 2L + 2W = 30 or L + W = 15. This gives us W = 15 – L.
Then we know that LW = A, where A is the area of the rectangle. So we can substitute for W into this equation and at least arrive at an expression for A that only involves the one variable L. This expression is A = L(15 – L). Now we can graph this function because it’s a parabola. And we know from past experience that (i) it is has a maximum value because the coefficient of L2 is negative; and (ii) it crosses the L-axis when L = 0 and L = 15.
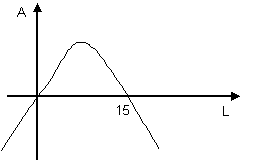
But parabolas have their axis of symmetry and maximum point, midway between the points where they cross the L-axis. So the axis of symmetry of the parabola above is at L = 7.5. This is also where its maximum point is.
But if L = 7.5, then W = 15 – L = 15 – 7.5 = 7.5. So W = L and the rectangle has to be a square.
Solution to the Extension
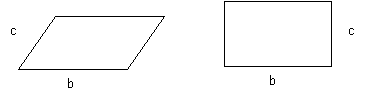
We do this in easy steps. First the rectangle of perimeter 30 cm with biggest area is a square. This has been done in the main problem. Second, a parallelogram with no internal angles of 90 has a smaller area than a rectangle with the same side lengths. To see this, consider the parallelogram and the rectangle below. Clearly the rectangle has area bc. The parallelogram has area base x height. Since its height is less than c, its area is less than bc. So the parallelogram has a smaller area than the rectangle even though they both have the same perimeters.
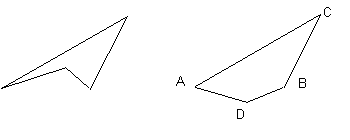
Third, a quadrilateral with an exterior angle less than 180° has a smaller area than a corresponding one with all exterior angles bigger than 180°. To see this, look at the diagram below. Clearly the quadrilateral on the right has the largest area yet they both have the same perimeters.
Fourth, the quadrilateral on the right above has smaller area than a quadrilateral whose diagonals are perpendicular. To see this, imagine that the points A and B are fixed and that A to C to B is a piece of string.Place a pencil inside the string at C. Move the pencil keeping AC and BC straight (taut). What is the biggest area of the triangle ABC? Well as C moves, the base AB remains the same. So the biggest area is found when the height of the triangle is the largest. This occurs when the perpendicular from C to AB goes through the midpoint of AB. Call this position for C, K. (Can you see that AK = KB?)
Notice that the quadrilateral formed by AKBD has the same perimeter as ACBD but AKBD has the bigger area.
We can do exactly the same thing with the point D. The position of D which makes triangle ABD have the biggest area is when D is above the midpoint of AB. Call this point L. Then the quadrilateral AKBL has the same perimeter as ABCD but it has a bigger area. What’s more, KL is perpendicular to AB.
Fifth, we want to show that among all quadrilaterals with the same perimeter and with perpendicular diagonals, the one with the biggest area is a parallelogram. Consider the quadrilateral below.
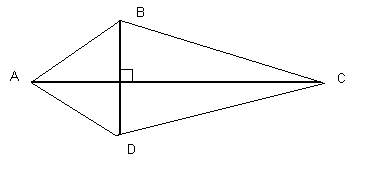
By the argument of ‘Four’, we can assume that AB = AD and that BC = CD. Now repeat the argument of ‘Four’ using B as the point to put the pencil and A and C as the fixed points. The argument we used above then shows that we can move B to a place above the midpoint of AC and in the process increase the area of triangle ABC. Repeating this on triangle ACD, we see that the area of this triangle is maximised when D is above the midpoint of AC. So we have a quadrilateral whose area is bigger than the original quadrilateral ABCD.
In this new quadrilateral, AB = BC = CD = DA. From here it is easy to show that opposite angles are equal and so the quadrilateral is a parallelogram (with equal sides – a rhombus).
Now lets' recap. We can show that among all rectangles with a given perimeter, the one with biggest area is a square. Then any other quadrilateral can be changed into another quadrilateral with the same perimeter and bigger area, using ‘Three’ and/or the ‘pencil’ approach of ‘Four’. What’s more this quadrilateral has to be a parallelogram. But we know that for every parallelogram with a given perimeter there is a rectangle with the same perimeter and a larger area. Hence among all quadrilaterals with a given perimeter, the square is the one with the biggest area.