Perfect Packing

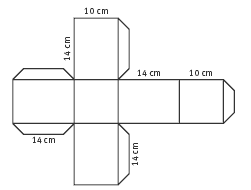
Question 1 is a straightforward task in which the students make a cuboid-shaped container that meets certain specifications. Encourage them to do the most professional job possible. The quality of the end product will depend on their:

• using pencil rather than pen for construction lines
• using a set square (or anything known to be square) when forming the right angles
• measuring accurately
• scoring lines before folding
• using suitable glue tabs
• using small quantities of PVA glue instead of sticky tape.

Like most nets, the net for the container can be drawn in more than one way.
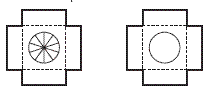
The inserts in question 2 are important, not only for stopping the egg moving inside the container, but also to provide protection for the egg. Most students will have come across similar inserts inside Easter egg boxes. Chocolate eggs are much more fragile than emu eggs, yet the thin card of a well-made container does an excellent job of protecting them.
The students have to decide how big to make the diameter of the hole in the insert. Perhaps the best way of doing this is to trace the outline of the egg pictured in the book, measure its length, divide this by 4, and then determine the width of the egg at the points 1/4 of the way from each end.

They should draw the circle using a compass centred on the point where the diagonals of the square insert cross. Instead of cutting out the hole, they could cut "fingers" radiating from the centre. This method allows for some error and small variations in egg size.
Question 2a asks the students how they could get precise dimensions for a specific egg. Various possibilities are suggested in the Answers, but some students may realise that the decision to place the inserts 1/4 of the way up each egg is probably an arbitrary one. If this is so, it may be easier to adjust the length of the four flaps on the insert than to keep playing around with the diameter of the hole.

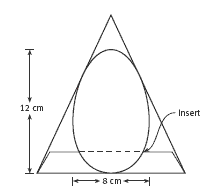
When answering question 3, the students could begin by drawing a sketch of the side view of the pyramid, starting with the emu egg itself. You could photocopy an egg shape about 12 centimetres by 8 centimetres and give this to them to work with. They will need to consider:

•  using an insert near the bottom of the pyramid to hold the egg in place
•  choosing a size for the base that wonÕt make the pyramid too tall
•  ensuring that the insert and the sloping sides fit neatly around the egg to prevent it from moving in transit
•  giving the egg appropriate protection in a container of this shape.

Finally, the students should discuss the merits of the square-based pyramid compared with the cuboid as a suitable container for the egg. As part of this discussion, they could consider how a number of pyramidshaped boxes would pack together.
As an extension, the students could investigate the design of containers used for hens' eggs, especially nonmoulded containers.
 

Answers to Activity

1. a. Here is one possible net:

b. Practical activity
2. a. Here are two possible nets:

Getting the diameter of the hole in the inserts just right is tricky. Possible methods include:

•  trial and improvement
•  using plastic putty to build a mould around the egg up to the quarter mark and measuring the required diameter from this
•  pressing the egg into packed, damp sand and measuring the diameter of the
• depression it has made
•  cutting "fingers" outward from the centre, bending these fingers at the required place, and using the position of the bends to determine the required diameter.

b. Practical activity. The bottom insert may need to have a larger hole than the top insert because of the shape of the egg.

3. The dimensions of the base would need to be greater than the width of the egg to allow the pyramid to hold the widest part of the egg. Similarly, the height of the triangular faces would need to be greater than the length of the egg. There would need to be an insert in the base to stop the egg moving.

Although attractive and unusual, this shape may not be very practical for an emu egg container. It would be:

• either very tall or very wide compared with the egg (especially if a centimetre gap is left around the egg to protect it)
• difficult to pack for postage ¥ difficult to pack with others
• difficult to make
• tricky to open (presumably the egg is removed through the base).