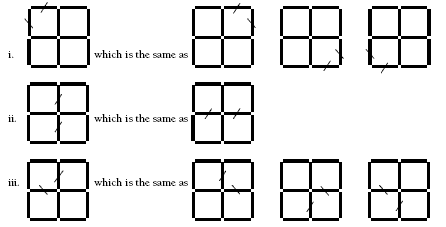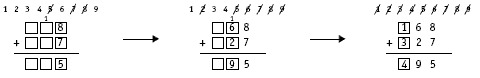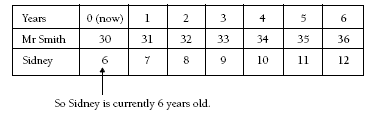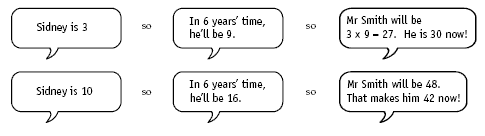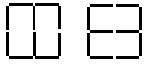Pattern Teasers

Problem One

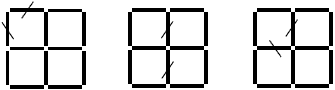
Students may want to solve this problem using nursery sticks as a physical model. The problem can be approached systematically in a number of ways.
Where might the two sticks be removed from?

Are the remaining shapes squares?
Removing two sticks leaves 10 sticks behind, which limits the possible sizes of the squares. A 2 x 2 square takes eight sticks. A 1 x 1 square takes four sticks. A combination of one each of these sizes seems the most likely, with two sides of the 1 x 1 square shared:

Students need to know the meaning of polygon to answer part b. The origin of polygon is “many angles”. Its meaning is a closed shape with an unspecified number of angles. The polygons in part b therefore must be bounded by sticks. This limits the places where two sticks can be removed from because every stick must be connected to another stick at both ends.
The sticks that can be removed are:

Option i leaves three squares.
Option ii leaves two rectangles.
Option iii leaves two squares (as in part a).

Problem Two

Encourage the students to record the strategies they use in developing their solutions. They could start by filling in the ones column. Remind them that putting six and seven in the ones column will result in a 10 being carried over to the tens column.
One strategy might be:

Note that in the second step of the example given above, nine is the crucial digit to place. It can’t go in the tens place of either addend because the carried 10 would mean that a digit is used twice.
Once students have found one solution, they can easily produce another by rearranging the columns.

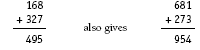
Problem Three

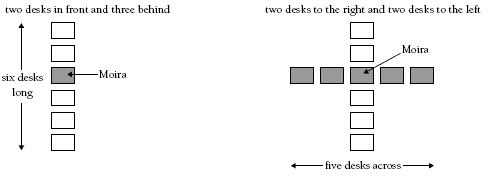
Students may like to use square tiles to represent the desks. They can build up the classroom as they consider the clues:

So, the full classroom is 6 desks x 5 desks = 30 desks. This is an example of a multiplication array. Students’ understanding of arrays can be enhanced by trying similar problems. For example, “In Angelo’s classroom, there are twice as many desks in each row across as there are in each line going down. There are 32 desks in total. How long is each row?”

Problem Four

Making a table is a useful strategy for solving this problem.

So

Similarly, students may use a trial and improvement strategy:

Students can improve their attempts until they find Sidney’s current age.

Answers to Problems

1. a. One solution would be:

b. Two rectangles

or any combination of 3 squares, for example:

2. There are a number of possible addition
equations, including 235 + 746 = 981, 168 + 327 = 495, 139 + 428 = 567,
278 + 316 = 594, 596 + 142 = 738, and 219 + 438 = 657. Manipulating the digits in each of these equations leads to others, such as 462 + 357 = 819, 782 + 163 = 945, and 281 + 394 = 675.
3. 30
4. 6