Ko te kaupapa nei, he tūhura i te tikanga o tēnei mea te pātapa, he whakamahi hoki i te pātapa hei whiriwhiri i te roa o ngā tapa me te rahi o ngā koki o tētahi tapatoru hāngai. Kia rua wiki pea te roa o tēnei kōwae ako. I takea mai tēnei kōwae ako i te kōwae ako reo Ingarihi Investigating the Idea of Tan.
Kia mōhio te ākonga:
- ki te whakamahi i ngā tikanga pātapa hei whakaoti rapanga e whai wāhi mai ana te tapatoru hāngai
- ki te whakaoti whārite pēnei i te tan(θ) = a, mēnā kei waenganui i te 0° me te 360° te koki θ?’
- ki te rahi o tan(θ) mō ēnei koki: 0°, 45°, 135°, 180°, 225°, 315°, 360°.
- kāore he uara o te tan(90°), me te tan(270°)
Whārangi Mahi 1
Whārangi Mahi 2
he tātaitai
he tāporowhita
he ine-koki
- Ko te mahi tuatahi, he tūhura i te tikanga o te pātapa (tan) o tētahi koki mai i te 0° ki te 90°.
Te mahi a te pouako
He tauira kōrero mā te pouako Tonoa mā ia ākonga e tuhi he papa kauwhata (ngā tuaka x, y) me tētahi porowhita. Kia 10 cm te pūtoro o te porowhita, ko te (0,0) te pokapū. Ka tuhi hoki i te rārangi pātapa o te porowhita x = 1. Tuhia he papa kauwhata, he tuaka x, y. Kia 12 cm pea te roa o ngā tuaka atu i te pokapū ki ngā ahunga e whā.
Tuhia he porowhita, kia 10 cm te pūtoro, ko te (0,0) te pokapū.
Tuhia te rārangi pātapa o te porowhita x = 10.
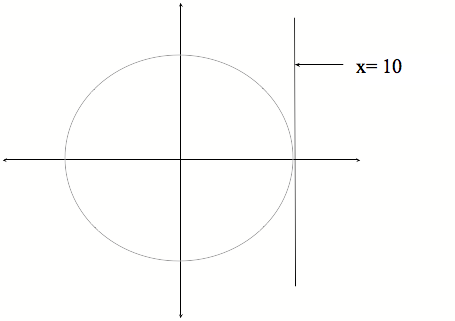
Whakamāramahia te tikanga o te pātapa o tētahi koki. Tuhia tētahi rārangi, atu i te pokapū kia haukoti i te rārangi x = 10.
Waitohua ko te ‘θ’ hei ingoa mō te koki kei waenganui i taua rārangi me te tuaka x
Ka kīia ko te pātapa o taua koki (tan θ) ko te wāhi e haukoti ai te rārangi i te pātapa x = 10.
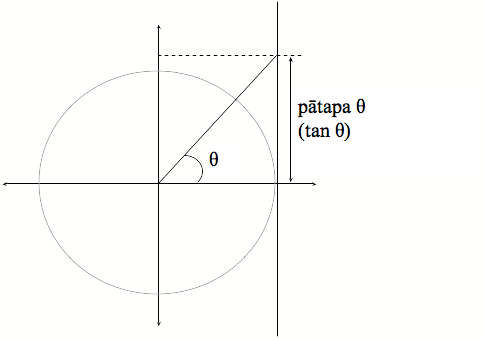
Ko te ‘tan’ hei tohu i te pātapa, he whakapotonga o te kupu Ingarihi ‘tangent’.
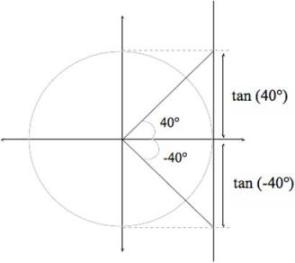
Tonoa ngā ākonga ki te kimi i te pātapa o te 40°.
Tuhia ngā uara o ēnei pātapa ki tētahi tūtohi.
Tātaihia te toharite o ngā inenga o ngā pātapa mō te 40°, ka tuhi atu ai ki te tūtohi.
Tuhia he rārangi atu i te pokapū, kia 40° te koki ki waenganui i taua rārangi me te tuaka x.
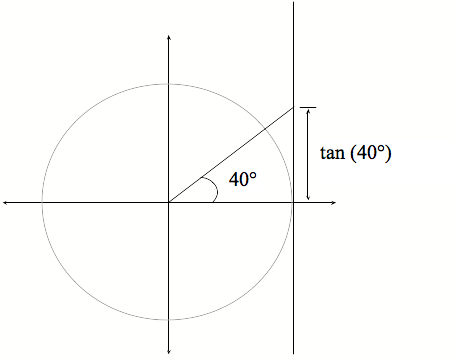
Inea te pātapa o te 40° (tan 40°). Māku e tuhi ā koutou inenga ki tētahi tūtohi:
te koki ngā inenga o te pātapa (cm) te
toharite40° 8.4, 8.2, 8.5, 8.4, 8.3,
8.3, 8.5, 8.4, 8.38.37 (2mi) Me pēhea te tātai i te toharite o ngā inenga mō te pātapa o te 40°? Tāpirihia ngā inenga, ka whakawehe ai ki te maha o ngā inenga: (8.4 + 8.2 + 8.5 + 8.4 + 8.3 + 8.3 + 8.5 + 8.4 + 8.3) ÷ 9
Kia pērā anō te kimi i te pātapa o te 45°, te 50°, me te 60°. Tuhia ki te tūtohi. te koki ngā inenga o te pātapa (cm) te
toharite40° 8.4, 8.2, 8.5, 8.4, 8.3,
8.3, 8.5, 8.4, 8.38.37 (2mi) 45° 50° 60° Tirohia te uara o te pātapa o ēnei koki te tātaitai, ka whakatairite ai ki ērā o ngā ākonga. Tirohia ā koutou tātaitai. Mēnā ka whakaurua te 40 (hei tohu i te koki 40°), kātahi ka pēhia te pūtohu ‘tan’, he aha te tau ka puta? Ko te 0.8390996
Koirā te uara o te pātapa o te 40°. He aha te hononga o tēnā ki tā koutou ine i te pātapa o te 40°? Tekau te rahinga ake o tā mātou inenga.
E tika ana kia 1 cm te roa o te pūtoro o te porowhita, ā, ko te rārangi x = 1 te rārangi pātapa, engari he iti rawa tēnā e tutuki ai ā tātou inenga. Nō reira i whakarahia ake mā te 10, kia ngāwari ai te mahi ine.
.jpg)
Kimihia te uara o te pātapa o te 45°, te 50°, me te 60°, ka tuhi ai ki te tūtohi.
te koki ngā inenga o
te pātapa (cm)te toharite te pātapa (tātaitai) 40° 8.4, 8.2, 8.5, 8.4,
8.3, 8.3, 8.5, 8.4, 8.38.37 (2mi) 0.839 (3mi) 45° 1 50° 1.192 (3mi) 60° 1.732 (3mi)
- Ko te mahi tuarua, he tūhura i te tikanga o te pātapa (tan) o tētahi koki mai i te 0° ki te -90°, mai i te 90° ki te 180°, mai hoki i te 180° ki te 360°.
Te mahi a te pouako
He tauira kōrero mā te pouako Tūhuratia te uara o te pātapa o ngā koki mai i te 0° ki te -90°. .jpg)
Tuhia te koki -40° ki te papa kauwhata. Inea te pātapa, māku e tuhi ki tētahi tūtohi.
te koki ngā inenga o te
pātapa (cm)te toharite te pātapa (tātaitai) -40° -8.4, -8.2, -8.5,
-8.4, -8.3, -8.3,
-8.5, -8.4, -8.3-8.37 (2mi) -0.839 (3mi) Tātaihia te toharite, ka kimi ai i te uara o te pātapa -40° ki te tātaitai.
Whakawhitiwhiti kōrero mō te hononga o te pātapa o tētahi koki mai i te 0° ki te 90°, me te koki e hāngai ana mai i te 0° ki te -90°. Tirohia te tūtohi i oti inanahi. E hia te pātapa o te 45°? Ko te tahi.
Nō reira, e hia te pātapa o te -45°? Ko te tahi tōraro (-1).
Whakaaturia tēnei hononga ki te papa kauwhata:
Whakaotia te tūtohi:
te koki te pātapa 10° 0.176 -10° 20° -20° 30° -30° 40° -40° 50° -50° 60° -60° 70° -70° Tūhuratia te pātapa o ētahi atu koki. Kua tuhia he rārangi ki te papa kauwhata, 135° te rahi o te koki kei waenganui i taua rārangi me te tuaka x. Kua whakaroatia te rārangi kia haukoti i te rārangi pātapa x = 1.
.jpg)
E hia te pātapa o te koki 135°? Ko te tahi tōraro (-1)
Ka taea tētahi whārite te tuhi hei whakaatu i ētahi hononga pātapa koki:
tan(135°) = tan (-45°) = tan(315°) = -1Whakaaturia te 315° ki te papa kauwhata:
.jpg)
Me mahi takirua ki te kimi i ētahi atu hononga pātapa. Hei tauira:
tan(170°) = tan (-10°) = tan(350°) = -0.176 (3mi) tan(10°) = tan (190°) = 0.176.jpg)
tan(30°) = tan (-210°) = 0.588 (3mi) tan(-30°) = tan (150°) = tan(330°) = -0.588 (3mi)
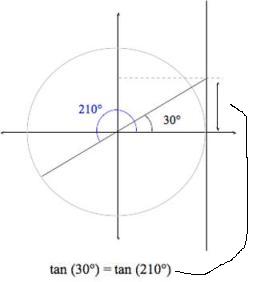
Tūhuratia te pātapa o te koki 90° me te 270°. Kimihia te uara o te pātapa 90° i te tātaitai. He aha ka puta mai? Ko tētahi tohu e mea ana, kāore he uara.
Whakaaturia ki te papa kauwhata, he aha e kore ai e puta he uara mō te tan(90°)
.jpg)
He whakarara te rārangi mō te 90° me te rārangi pātapa, nō reira e kore rawa e haukoti.
-
- Ko te mahi tuatoru, he whakaū ngā mahi o runga ake nei, mā te tūhura i ēnei pātai. He pai te mahi takirua, tonoa hoki ngā ākonga ki te whakamārama i ā rātou whakautu, ki te whakaatu rānei i ā rātou whakautu ki te papa kauwhata.
- He aha e māmā ai te kimi i te uara o tan(0°)?
- He aha tētahi atu koki e ōrite ana te pātapa ki te tan(0°)?
- He aha e māmā ai te kimi i te uara o tan(135°)?
- He aha ētahi atu koki e whai pānga ana te pātapa ki te tan(135°)?
- Whakamāramatia mai ngā piki me ngā heke o ngā pātapa mai i te 0° huri āwhio ki te 360°?
- Ka ahatia te pātapa ina pātata haere te koki ki te 90°, ki te 270° rānei.
- Mēnā ko te 1.5 te pātapa o tētahi koki, tuhia he hoahoa āwhata hei kimi i te rahi o te koki.
- He aha ngā koki he tōrunga te pātapa?
- He aha ngā koki he tōraro te pātapa?
- Mēnā e mōhio ana koe ki te pātapa o te 10° (tan(10°) = 0.176), he aha ētahi atu koki ka taea te uara o te pātapa te whakaatu?
- Whakamahia he tātaitai, ka whakaoti ai i te tūtohi nei (whakaawhiwhia kia 1 te mati ā-ira)
te koki 10° 20° 30° 40° 50° 60° 70° 80° 90° te pātapa te koki 100° 110° 120° 130° 140° 150° 160° 170° 180° te pātapa te koki 190° 200° 210° 220° 230° 240° 250° 260° 270° te pātapa te koki 280° 290° 300° 310° 320° 330° 340° 350° 360° te pātapa - Whakaaturia ngā pātapa o ngā koki mai i te 0° ki te 360° ki tētahi kauwhata.
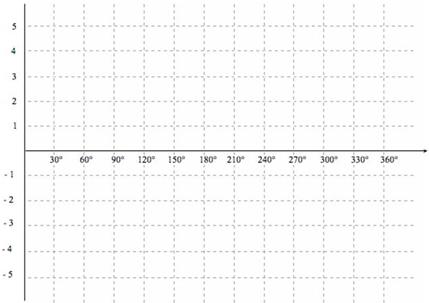
- Ko te mahi tuawhā, he whakamahi i te pātapa hei kimi i te tapa, i te koki rānei o tētahi tapatoru.
Te mahi a te pouako He tauira kōrero mā te pouako Tūhuratia te whakamahinga o te pātapa hei kimi i te roa o tētahi tapa o tētahi tapatoru hāngai. Titiro ki te papa kauwhata nei. E rua ngā porowhita e whakaaturia ana, me ngā rārangi pātapa.
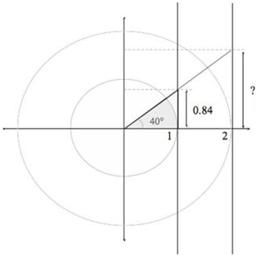
Kua tuhia he rārangi 40°. E whakaaturia ana te uara o te pātapa o te 40° (mai i te tātaitai). Koia hoki te roa o tērā taha o te tapatoru hāngai
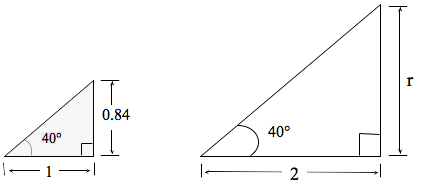
Me pēhea te tātai i te roa o te tapa e tohua mai ana ki te ‘r’? E rua te whakareatanga ake o te tapatoru nui, tērā i te tapatoru iti. Nō reira, ka whakareatia te 0.84 ki te 2 hei kimi i te roa o tērā tapa. Arā te tātaitanga:
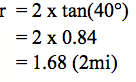
Hoatu te - Whārangi Mahi 1 (PDF, 182KB) hei whakaoti mā ngā ākonga.
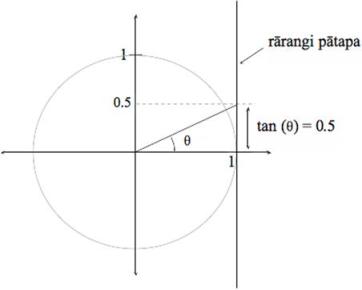
Whakamāramatia te tohu tan-1, me te whakamahinga o tēnā pūtohu o te tātaitai hei kimi i te uara o tētahi koki. Titiro ki te papa kauwhata nei. Ko te 0.5 te pātapa o te koki kua tapaina ki te ‘θ’. He aha te whakatau tata (mā te tirotiro noa iho) mō te rahi o te koki? ākene pea ko te 30°. He iti ake i te 45°.
āe kei te takiwā pea o te 30°. Whakaurua te 0.5 ki te tātaitai, kātahi ka pēhi i te pātene mō te tan-1 . Ka puta ko te rahi o te koki. Ko te pātapa kōaro te ingoa Māori mō te tan-1 . Me pēnei te tuhi i te tātaitanga:
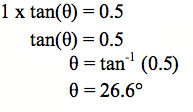
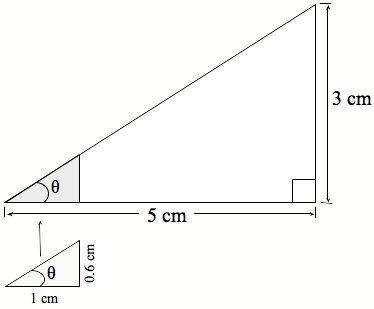
Hoatu ētahi atu tauira hei kimi mā ngā ākonga i te rahi o te koki o tētahi tapatoru hāngai. Anei anō ētahi tauira:
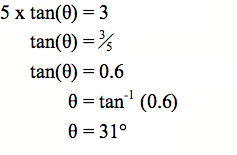
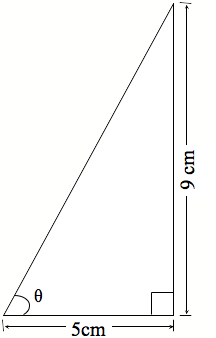
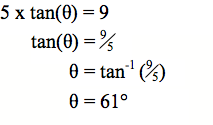
Hoatu te - Whārangi Mahi 2 (PDF, 147KB) hei whakaoti mā ngā ākonga.