The purpose of this activity is to engage students in an investigation of parabolas in a practical context.
This activity assumes the students have experience in the following areas:
- Factorising and expanding quadratic expressions.
- Graphing relations and functions on a Cartesian Plane.
The problem is sufficiently open ended to allow the students freedom of choice in their approach. It may be scaffolded with guidance that leads to a solution, and/or the students might be given the opportunity to solve the problem independently.
The example responses at the end of the resource give an indication of the kind of response to expect from students who approach the problem in particular ways.
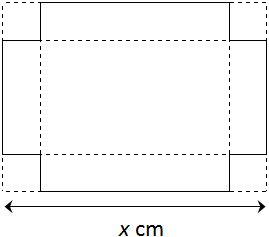
Task: A rectangular sheet of card, with perimeter = 80 cm is made into an open-topped box, by folding in 2 cm x 2 cm squares from each corner. Investigate the relationship between x, the length of one side of the card and C, the capacity of the box.
The following prompts illustrate how this activity can be structured around the phases of the Mathematics Investigation Cycle.
Make sense
Introduce the problem. Allow students time to read it and discuss in pairs or small groups.
- Do I understand the situation and the words? (Students may need to build a single open box to make sense of the requirements.)
- What varies in the problem and what stays the same? (The size of the cut-out squares and the perimeter of the rectangular paper stay constant. The dimensions of the rectangular paper vary)
- Does this look/sound like a problem I have worked on before? (Student may have encountered optimisation problems before.)
- What will my solution look like? (The solution give the dimensions of the rectangular paper that yield the open box with greatest volume.)
Plan approach
Discuss ideas about how to solve the problem. Emphasise that, in the planning phase, you want students to say how they would solve the problem, not to actually solve it.
- What are the maths skills I need to work this out? (Students will need to recognise that rectangles with equal perimeters can have different areas. That means the boxes are likely to have different volumes.)
- What could the solution definitely not be? (Set sensible bounds for the sides of the rectangular paper.)
- How could I show this problem using numbers, calculations, pictures, graphs, tables or materials?
- Do I know how to calculate areas of rectangles, and volumes of cuboids?
- What tools (digital or physical) could help my investigation?
Take action
Allow students time to work through their strategy and find a solution to the problem.
- Have I shown my workings in a step-by-step way? Have I organised my results systematically to look for patterns?
- Have I got enough examples? Have I got all the examples that are possible?
- How could I make sure that I haven’t missed anything?
- Are there relationships in my results? (What happens to volume as the rectangular paper gets ‘skinnier’?)
- Can I use algebra to represent area and volume with x as a variable?
- Can I solve equations to find the maximum volume possible?
- Could I graph the relationship between x and volume? What will the graph show?
Convince yourself and others
Allow students time to check their answers and then either have them pair share with other groups or ask for volunteers to share their solution with the class.
- What is the solution? Can I justify that I have found the maximum volume?
- Is my working clear for someone else to follow?
- How would I convince someone else I am correct?
- Could I have solved the problem in a more efficient way, such as using algebraic formulae?
- How might the efficient algebraic or graphic strategy be used for similar problems?
Examples of work
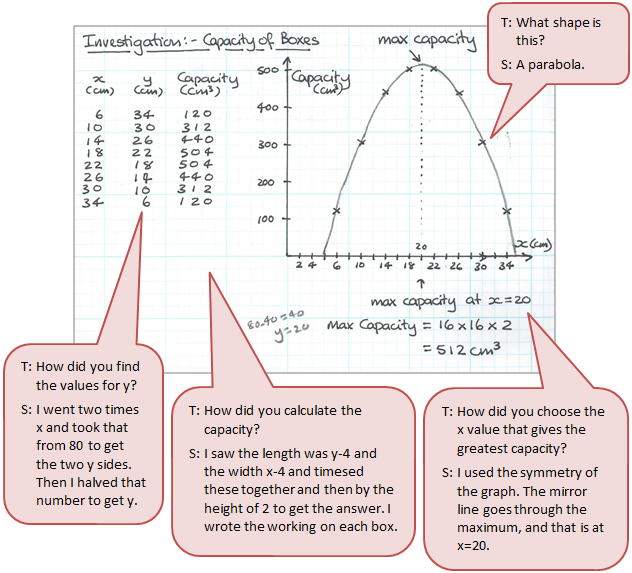
Work sample 1
The student makes and measures concrete examples to lead them to solve the problem. They link the practical task to a generalised model.
Click on the image to enlarge it. Click again to close.
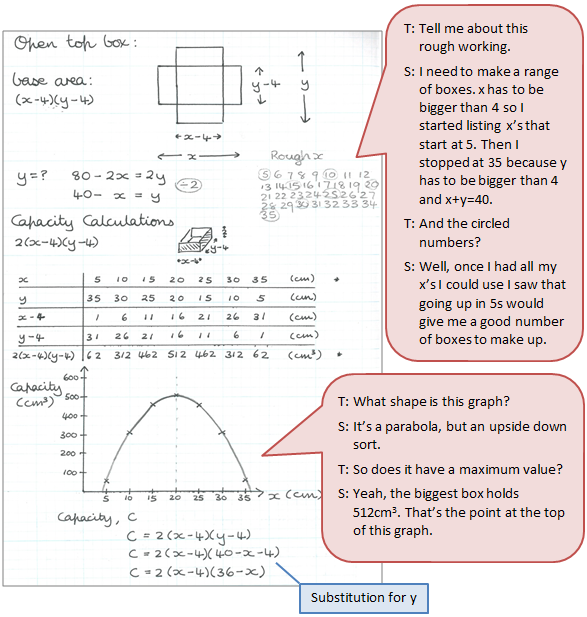
Work sample 2
The student carries out directed calculations that will lead them to find a quadratic relationship.
Click on the image to enlarge it. Click again to close.
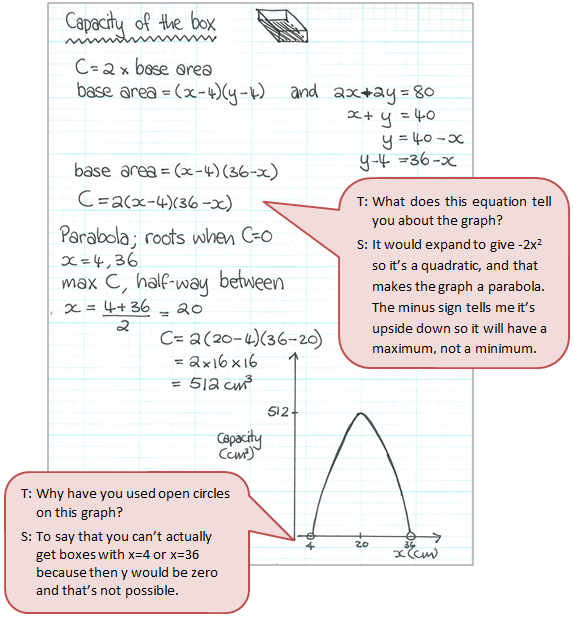
Work sample 3
The student carries out an algebraic investigation that allows them to describe a quadratic relationship.